Es lebe die Geometrie!

Haupt-Sehnen bei Zykloiden

Unter einer k-Zykloide verstehen wir den Graphen der Funktion
() mit der Periode in einer Darstellung mit komplexen Zahlen. Die Punktmenge
des Graphen ist also.
Dies ist die Spur eines Punktes auf dem Rand eines Kreises ('Gangkreis' oder 'Rollkreis' genannt) vom Radius
1/k, der ohne zu Rutschen an einem Kreis ('Rastkreis') vom Radius 1 abrollt, und zwar an der Außenseite diese
Kreises für k > 0 und an der Innenseite für k < 0.
Die Sehne, die einen Kurvenpunkt mit dem Punkt verbindet, nennen
wir 'm-Hauptsehne', weil sie besondere geometrische Eigenschaften hat. Dabei ist m ganzzahlig, aber nicht
durch k+1 teilbar. Die Länge der m-Hauptsehne ist , hängt also nicht von ab. Dies
ist die Länge einer Sehne in einem Kreis vom Radius , dessen zugehöriger Mittelpunktswinkel
ist, die also Seite eines regulären n-Ecks mit dem Betrag von k+1 als Eckenzahl n und der Überschlagungszahl
m ist. Bei der Untersuchung der m-Hauptsehnen kann man sich auf m-Werte zwischen 1 und floor((m+1)/2)
(= größte ganze Zahl kleinergleich (m+1)/2) beschränken, da jede Sehne zu einem anderen m-Wert mit einer
Sehne zu diesem Bereich übereinstimmt. Ihr Richtungswinkel ist . Neben den Hauptsehnen gibt es
stets andere Sehnen mit gleicher Länge.

Der Pol der m-Hauptsehne ist der Schnittpunkt der Tangenten in den Endpunkten der Sehne.
Er wird unabhängig von m in komplexer Form durch bestimmt und durch
in kartesischer Darstellung. Der geometrische
Ort der Pole (die 'Polkurve') ist für alle k-Zykloiden ein Kreis um den Ursprung mit dem Radius
1+2/k. Der Kreis stimmt mit dem Rastkreis der Bogenmitten-Evolvente der k-Zykloide überein.
Im Punkt C schneiden sich die Tangenten in A und B unter einem Winkel der Größe . Dies
ist die Größe des Mittelpunktwinkels beim Umkreis des oben genannten n-Ecks. Die Geraden CA
bzw. CB schneiden die Polkurve außer in C in einem zweiten Punkt G bzw. H. Dabei teilt der Punkt
A bzw. B die Strecke CG bzw. CH im Verhältnis (k+1) : 1. Der Betrag von (k+1) ist also der Faktor,
mit dem man den Abstand GA multiplizieren muss, um den Abstand CA zu erhalten. Dabei liegt A bzw.
B für k > 0 innerhalb der Strecke CG bzw. CH und für k < 0 außerhalb. Die Strecke GH ist parallel zur
Strecke AB und die Längen verhalten sich wie (k+2) : (k+1).

Der Momentanpol der m-Hauprsehne ist der Schnittpunkt der Normalen (orthogonal zu den Tangenten)
in den Endpunkten der Sehne. Er wird durch bestimmt. Der geometrische Ort dieser Punkte,
die Rastpolkurve, ist also ein Kreis vom Radius 1. Die zugehörige Gangpolkurve ist ein Kreis mit der
Strecke zwischen D und dem Pol C als Durchmesser. Sein Radius beträgt also und seine Mitte
durchläuft einen Kreis vom Radius .

Die Enveloppe der m-Hauptsehnen ist nur für bei ungeradem k eine Zykloide, und zwar eine
{-k;+k}-Zykloide mit dem Funktionsterm . Allgemein wird sie mit
der Bezeichnung durch folgenden Funktionsterm mit der Variablen dargestellt: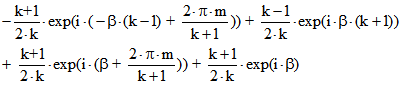


Im Allgemeinen ergibt sie sich also als Bahn einer Überlagerung von vier gleichförmigen Kreisbewegungen.

Die erste Periode der Animation zeigt die -3-Zykloide (Steiner-Zykloide) mit einer 1-Hauptsehne mit der
Länge 4/3 zwischen den Punkten und . Der Pol C wird in komplexer
Darstellung durch gegeben und der Momentanpol D durch . Die hellblaue Polkurve ist ein
Kreis um den Ursprung mit dem Radius 1/3 und die hellgrüne Rastpolkurve hat den Radius 1. Die Enden
A und B der schwarzen Sehne bilden mit dem Pol C ein rechtwinkliges Dreieck, dessen Katheten durch
die Polkurve halbiert werden. Die dunkel grüne Gangpolkurve ist ein Kreis vom Radius 2/3, der AB als
Durchmesser hat und dessen Mitte auf der Polkurve liegt. Dies ist eine Besonderheit der Steiner-Zykloide.
Die Enveloppe der Hauptsehnen stimmt mit der Steiner-Zykloide überein. Darum berührt die Sehne die
-3-Zykloide im Punkt H, in dem die Gerade AB die Verbindungsgerade von den Spitzen der blauen Pfeile
schneidet. Diese Pfeile sind die Komponenten der roten Geschwindigkeits-Vektoren senkrecht zur Sehne.
Die weißen Pfeile in Richtung der Sehne sind gleich lang, weil die Sehnenlänge konstant bleibt. H ist der
Fußpunkt des Lots von D auf AB. Bei Spiegelung von H an der Sehnen-Mitte ergibt sich der Fußpunkt
des Lots vom Pol C auf AB.

Die zweite Periode der Animation zeigt die -4-Zykloide (Astroide) mit einer 1-Hauptsehne mit der Länge
zwischen den Punkten und , die den Pol und
den Momentanpol hat. Die Polkurve ist ein Kreis mit dem Radius 1/2, die Momentanpolkurve ist
auch hier ein Kreis mit dem Radius 1, und die die Gangpolkurve ist ein Kreise vom Radius 3/4. Die Tangenten
in A und B schneiden sich in C unter dem Winkel der Größe 60° und haben weitere Schnittpunkte G und H
mit der Polkurve, die von C 2/3 so weit entfernt sind wie A und B.
Die blaue Enveloppe der Sehnen ist hier keine Zykloide.

Die Bilder der auf die Animation folgenden Gleitschau zeigen dazu Standbilder. In Bild 3 und 7 sind in Orange
die Evoluten der k-Zykloiden einzeichnet, die selbst k-Zykloiden sind. Die Strecke AD berührt die Evolute im
Punkt A*, der Mittelpunkt des Krümmungskreises der roten Zykloide im Punkt A ist. Entsprechendes gilt für
B. Die schwarz gezeichnete Strecke A*B* ist Hauptsehne der Evolute mit dem hellgrünen Kreis als Polkurve.
Die Längen der beiden schwarzen Sehnen verhalten sich wie k : k+2.

Die erste Periode der Animation zeigt eine 1-Zykloide (Kardioide) mit einer 1-Hauptsehne der
Länge 4 zwischen den Punkten und Der Pol ist , die
Polkurve folglich ein Kreis um den Ursprung mit dem Radius 3. Der Momentanpol ist , die
Rastpolkurve ein Kreis vom Radius 1 und die Gangpolkurve ein Kreis vom Radius 2. Wie bei der
Steiner-Zykloide ist ABCD ein Rechteck. Die Tangente in A bzw. B schneidet die Polkurve in einem
weiteren Punkt G bzw. H , der 3/2 mal so weit von C entfernt ist wie A bzw. B. Wie bei der Steiner-
Zykloide ist A von C doppelt so weit entfernt wie von G, aber bei der Kardioide teilt A die Strecke
CG innen statt außen. Alle Hauptsehnen gehen durch die Spitze (1 ; 0) der Kardioide. Ihre Enveloppe
muss man sich darum durch diese Spitze ersetzt denken.

Die zweite Periode zeigt eine 2-Zykloide (Nephroide) mit einer 1-Hauptsehne der Länge
durch die Punkte und , mit dem Pol , dem Momentanpol
, dem Pol-Kreis-Radius 2 und dem Rastkreis-Radius 1. Wie bei der Astroide hat der Winkel
bei C im Dreieck ABC die Größe 60° oder 120°. A bzw.B ist bei der Nephroide wie bei der Astroide
von C dreimal so weit entfernt wie vom Pol-Kreis-Punkt G bzw. H, liegt hier aber zwischen C und G.
Die blaue Enveloppe der Hauptsehnen ist keine Zykloide.

In Bild 3 und 7 der Gleitschau sind auch hier die Evoluten eingezeichnet.

In dieser Bildfolge sind k-Zykloiden paarweise hintereinander angeordnet, für die der Betrag n von
k+1 übereinstimmt. Dabei wurden m-Hauptsehnen eingezeichnet, die regelmäßiges n-Ecke bilden mit
m als Überschlagungszahl. m ist also die Anzahl der Eckpunkte, die man auf dem Umkreis des n-Ecks
weiterrücken muss, um von einem Sehnen-Anfangspunkt zum zugehörigen Endpunkt zu kommen. Für
k = 5 und m = 2 ist das n-Eck z.B. ein zweifach überlagertes Dreieck und für k = 5 und m = 3 ein dreifach
überlagertes Zweieck. Der Umkreis des n-Ecks ist die dunkelgrüne Gangpolkurve, die an der hellgrünen
Rastpolkurve abrollt, wenn die Sehnen-Endpunkte sich auf der Zykloides weiterbewegen. Der Berührpunkt
D der beiden grünen Kreise ist der Momentanpol dieser Bewegung. Darum sind alle Verbindungsgeraden
von D mit den Sehnen-Endpunkten orthogonal zu den Tangenten in diesen Punkten. Alle diese Tangenten
gehen durch den gemeinsamen Pol C aller Sehnen des n-Ecks. In C berührt die hellblaue Polkurve die
dunkelgrüne Gangpolkurve. Die Zentren der n-Ecke liegen alle auf dem gelben Kreis um den Ursprung
mit dem Betrag von 1/k als Radius.