Es lebe die Geometrie!

Laguerre-Spiegelungen 1

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum I'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf


Ein ins Unendliche reichender Zylinder ermöglicht es, zu jedem Punkt A außerhalb der Zylinder-Fläche eine
Spiegelung zu definieren, die drei kollineare Punkte stets in drei kollineare Punkte abbildet, A festlässt und
jeden Zylinder-Punkt in einen Zylinder-Punkt abbildet. Durch diese Eigenschaften ist eindeutig bestimmt.
Das Bild Q eines Zylinderpunkts P ist der zweite Zylinderpunkt auf der Geraden AP, vorausgesetzt dass AP
nicht Tangente des Zylinders ist, sonst ist Q = P. Durch diese Bilder für Zylinderpunkte und die Kollinearitäts-
Eigenschaft sind auch die Bilder aller anderen Raum-Punkte festgelegt. Dass wird auf dieser Seite dargestellt.
ist involutorisch, das heißt: Wenn Q das Bild von P ist, dann ist P das Bild von Q. Wenn man den Zylinder
durch eine Kugel ersetzt, können Spiegelungen entsprechend definiert werden. Wir nennen die Spiegelungen
beim Zylinder 'Laguerre-Spiegelungen', weil sie eng mit involutorischen Abbildungen in der Geometrie der
Zykeln und Speere zusammenhängen, die Edmond Laguerre (1834-1886) entwickelt hat.

In dieser Animation ist der magentafarbene Punkt A das Spiegelungs-Zentrum. Es soll dargestellt
werden, wie sich für den mit zwei Kreisen markierte hellgrüne Punkt P der analog markierte orangene
Punkt Q als Spiegelungsbild von P aus Spiegelbildern von Punkten auf der Zylinderfläche ergibt. Dazu
wird ein ebenfalls hellgrüner Hilfspunkt R auf dem hellgrünen Kreis K in der Zylinderfläche benutzt.
Sein Bild bei Spiegelung an A ist der orangefarbene Punkt S auf dem Zylinder. R wird durch die
Spiegelung mit dem Zentrum P in den dunkelgrünen Punkt T auf dem Zylinder abgebildet, der dann an
A in den braunen Punkt U gespiegelt wird. Der gesuchte Bildpunkt Q bei Spiegelung von P an A ist
dann der Schnittpunkt der Geraden SU und AP. Diese beiden Geraden treffen sich im Raum, weil alle
konstruierten Punkte in der von A, P und R aufgespannten Ebene liegen.

Es ist nicht selbstverständlich, dass man nicht zu einem anderen Spiegelungspunkt Q gelangt, wenn man
einen anderen Hilfpunkt R auf dem Zylinder wählt. Dass dies der Fall ist, soll in der Animation dadurch
verdeutlicht werden, dass R sich auf dem Kreis K bewegt, ohne dass sich Q verrückt. Dabei wird durch
die Projektion in die xy-Ebene klar, dass dahinter ein geometrischer Satz beim Kreis in der Ebene steckt.
Auch wenn sich R auf einer Parallelen zur z-Achse bewegt, ändert sich die Lage von Q nicht. Dies folgt
aus dem Strahlensatz.

Bei der Bewegung von R auf dem Kreis K werden die Spuren der Punkte S, T und U aufgezeichnet. Es
sind Ellipsen. Die Spur zu S ist das Bild von K bei der Spiegelung an A, die Spur von T das Bild von
K bei der Spiegelung an P, und die Spur von U ergibt sich aus K durch die Hintereinanderschaltung
der Spiegelungen an P und A.

Um die Spiegelung an A im Rahmen der analytischen Geometrie zu beschreiben, geht man von der
Gleichnung aus, die genau für die Punkte (x;y;z) gilt, die auf der Zylinder-Fläche
liegen. Die Formel für die Spiegelung an A wird einfacher, wenn man sie im Rahmen der projektiven
Geometrie beschreibt. Dann ersetzt man das Punkt-Tripel (x;y;z) durch ein Quadrupel (x;y;z;1)
oder ein Quadrupel mit einer reellen Zahl s ungleich Null. Die Gleichung des
Zylinders kann dann in der äquivalenten Form geschrieben werden.
Wenn man den Punkt P also mit dem Quadrupel bezeichnet, liegt P bei dieser
Schreibweise genau dann auf der Zylinder-Fläche, wenn ist. Die zu der
Quadratform gehörige symmetrische Bilinearform f bildet ein Paar (p;a) von
Quadrupeln auf die reelle Zahl ab. Mit dieser Bilinearform f hat die Spiegelung
am Punkt A mit dem Quadrupel die folgende algebraische Form:
(*) .
Der Spiegelungs-Term ist nur dann definiert, wenn ungleich Null ist, also
wenn A nicht auf der Zylinder-Fläche liegt. Der Term ist linear in p. Das bedeutet: Für Quadrupel
p und q und reelle Zahlen s und t gilt wegen

.
Daraus folgt, dass bei dieser Abbildungsvorschrift wirklich drei kollineare Punkte in drei kollineare
Punkte abgebildet werden. Dass A dabei fest bleibt, folgt aus .
Aus

folgt für einen Punkt P auf der Zylinder-Fläche , so dass auch sein
Spiegelbild auf der Zylinder-Fläche liegt.

Bei der Benutzung dieser Spiegelungs-Formel kann man die vierte Komponente von p und a für
endliche Punkte auf 1 setzen, muss aber bedenken, dass dann die vierte Komponente von
nicht 1 ist, sondern ist. Erst die Teilung des Quadrupels durch
diese Zahl führt auch beim Bild-Quadrupel zur vierten Komponente 1.

Eine übersichtliche Darstellung für erhält man mit Hilfe der Maß-Matrix ,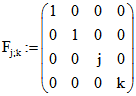
die auch in dem im Kopf dieser Seite genannten Text benutzt wird. Für j = 0 und k = -1 kennzeichnet
diese Matrix die metrischen Eigenschaften der Laguerre-Geometrie, denn es gilt ,
wobei p für die Matrix aus einer Zeile steht, für die dazu transponierte Matrix aus einer Spalte und
der tiefgestellte Punkt wie in dem Softwarepaket Mathematica die Matrix-Multiplikation bezeichnet.
Dann ist , wobei die quadratische Matrix mit vier Einsen in der
Haupdiagonalen und sonst nur Nullen bezeichnet.

Die Spiegelung an A bildet vier Punkte, die in einer Ebene E liegen, in vier Punkte einer Ebene E*
ab, die als Bild-Ebene von E angesehen wird. sei das Quadrupel,. das die
Koordinaten-Darstellung von E beschreibt, weil E die Menge der Punkte P ist, für die
gilt. Die Koordinaten-Darstellung von E* ist dann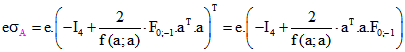
.

Leider kann man nicht mit Hilfe einer Formel wie die Formel (*) für darstellen.
Das liegt daran, dass die Matrix nicht invertierbar ist. Anders ist es, wenn man den Zylinder durch
eine Einheits-Kugel ersetzt. Dann muss nämlich in dieser Maß-Matrix die Null in der Hauptdiagonalen
durch Eins ersetzt werden, so dass die Matrix invertierbar wird. Sie ist dann sogar involutorisch, so
dass die gleiche Formel für Punkte und Ebenen anwendbar ist. Dieser Unterschied in der Geometrie
von Zylinder und Kugel hat zur Folge, dass es für Ebenen-Quadrupel d und e bei der Laguerre-
Spiegelung keine Formel gibt, die der Formel für Punkte-Quadrupel
p und q entspricht. Stattdessen errechnet man für Ebenen-Quadrupel und
mit dritter Komponente 1 in beiden Quadrupeln die Formel
.
Diese Formel bedeutet geometrisch, dass die Bildzykeln der Zylinder-Ellipsen D und E zu den
Quadupeln d und e bei der Blaschke-Abbildung das gleiche Tangentialabstands-Quadrat haben wie die
Bildzykeln der Zylinder-Ellipsen zu den Quadrupeln und . Unter 'Tangentialabstand' versteht
man dabei den Abstand der Berührpunkte eines gemeinsamen Tangenten-Speers zu zwei Zykeln. Denn
die Bildzykeln von D und E haben die Mittelpunkte und und die signierten
Radien und . Die Zykeln haben genau dann den Tangentialabstand Null, wenn sie sich berühren
Dann berühren sich auch die zugehörigen Zylinder-Ellipsen. Leider funktioniert diese geometrische Deutung
von als Tangentialabstands-Quadrat nur für Zykeln, die einen gemeinsamen Tangenten-Speer
haben, was zum Beispiel bei einem Zykel nicht der Fall ist, der in seinem Innern den zweiten Zykel enthält.

In der euklidischen Geometrie benutzt man eine Maß-Matrix mit drei Einsen in der Hauptdiagonalen
und einer Null an vierter Stelle, anstatt einer Null an dritter Stelle wie in der Laguerre-Geometrie. Denn
Ebenen D und E sind genau dann orthogonal, wenn die symmetrische Bilinearform

für die Ebenen-Quadrupeln d und e Null wird. Bemerkenswert ist dabei, dass dann die Formel
mit f ' statt f nur dann einen Sinn ergibt, wenn man unter p und a nicht
Punkt-Quadrupel versteht, sondern Ebenen-Quadrupel. Wir benutzen darum die Bezeichnung
mit kleinem a. Dann gilt für Ebenen-Quadrupel d und e.
Für Punkt-Quadupel p und q gilt hier dagegen die Formel
.

In dem im Kopf dieser Seite genannten Text wird eine gemeinsame Darstellung von Geometrien
zur Maß-Matrix gegeben, wobei j und k möglichst nicht spezialisiert wurden. Darum wird dort
die Formel (*) auch im Fall j = 0 und k = -1 für Ebenen-Quadrupel benutzt. In dieser Geometrie sind
dann also die Rollen von Punkte und Ebenen vertauscht. Dadurch ergibt sich in algebraischer Hinsicht
kein wesentlicher Unterschied, für die geometrische Vorstellung aber schon. Man kann dieses Problem
umgehen, indem man die Laguerre-Spiegelung mit Hilfe der auf der Seite ' Nullpolarität' erklärten
Abbildung transformiert. Die Abbildung von Ebenen-Quadrupeln kann bei dieser Nullpolarität mit Hilfe
der Matrix 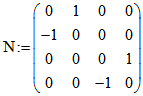transformiert werden. Die Matrix -N mit umgedrehten Vorzeichen ist
invers zu N und bildet die Punkt-Quadrupel ab. Die Transformation geht folgendermaßen: P mit dem
Quadrupel p sei die Kegelspitze zu einem Zykel ZD, der zu einer Zylinder-Ellipse D gehört. P bildet
man zunächst durch auf die Ebene von D ab, spiegelt diese dann mit und bildet die gespiegelte
Ebene schließlich mit zurück in den Raum der Kegelspitzen ab. Die Matrix der Hintereinanderschaltung
ist dann .
E sei nun die Ebene, die A bei der Nullpolarität zugeordnet ist. Sie hat das Quadrupel ,
so dass also gilt. Wegen errechnet man für die transformierte Matrix
.
Dies ist die Matrix der Spiegelung an der Ebene E für Punkt-Quadrupel bei Verwendung der Maß-Zahlen
j = -1 und k = 0. Für Ebenen-Quadrupel benutzt man die dazu transponierte Matrix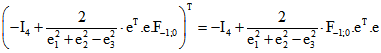
,
die zu einer Abbildung gehört, welche der Zuordnung (*) entspricht.

Neben der Spiegelung an Ebenen gibt es in der euklidischen Geometrie auch die Spiegelung an Punkten
nach der einfachen Formel für Punkte-Quadupel p und a. Dabei sind die Punkte P, A
und der Bildpunkt P* kollinear. A wird auf sich abgebildet und es gilt .
Wenn Q dabei auf Q* abgebildet wird, ist .

In der Laguerre-Geometrie ergibt die entsprechende Formel einen Sinn, wenn man
unter d und a Quadrupel von Ebenen versteht, die zu Zylinder-Ellipsen D und A gehören. Die Ebene der
Bild-Ellipse D* geht dann durch die Schnittgerade von D und A, und A wird auf sich abgebildet. Wenn
eine Ellipse E dabei auf E* abgebildet wird, ist . Da die Abbildung
außerdem involutorisch ist, also die Hintereinanderschaltung mit sich selbst die identische Abbildung ergibt,
kann sie als Laguerre-Spiegelung an der Ellipse A angesehen werden. Für ist die Matrix
zur Abbildung von Ebenen-Quadrupeln 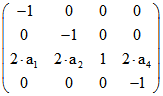, für Punkte-Quadrupel ist sie dazu
transponiert. Wenn P, Q und R drei Punkte in der Ebene zu A sind, für deren Laguerre-Spiegelungen ,
und die Vertauschungs-Relationen , und gelten, dann
ist die Spiegelung an A gleich . Durch die Tranformation von mit erhält man die
zugehörige Spiegelung der Kegelspitze S eines Zykels ZD an der Kegelspitze T eines Zykels ZA,
nämlich . Diese Abbildung stimmt mit der euklidischen Punktspiegelung überein.

Analog wie in der euklidischen Geometrie ist die Hintereinanderschaltung der Spiegelungen an drei Ellipsen
ebenfalls eine Spiegelung gleicher Art. Bildet man die zugehörigen vier Ebenen mit der Nullpolarität auf
Punkte des Raumes ab, so bilden sie ein Parallelogramm. Projiziert man diese Punkte parallel zur z-Achse
auf die xy-Ebene, so erhält man das Parallelogramm aus den Mittelpunkten der Zykel, die sich bei der
Blaschke-Abbildung der Ellipsen ergeben. Die Differenz der Radien zweier dieser Zykel stimmt mit der
Differenz der Radien von den andern beiden überein.

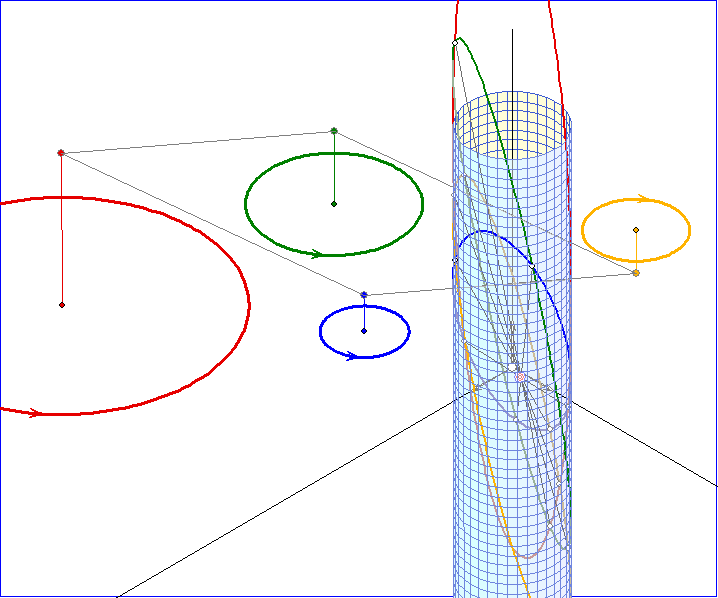
Die ersten drei Bilder der Gleitschau zeigen Zylinder-Ellipsen D, E, F und G mit den Zykeln ZD, ZE, ZF
und ZG . Dabei ist die Laguerre-Spiegelung an G die Hintereinanderschaltung der Laguerre-Spiegelungen
an D, E und F . Wenn , und die Quadrupel der Ebenen
zu D, E und F sind, dann hat die Ebene von G das Quadrupel .
g ist also die alternierende Summe von d, e und f. Alle vier Ebenen der Ellipsen haben den dreifach umkreisten
Punkt C0 im Innern des Zylinders gemeinsam. Das vierte Bild zeigt die Anordnung aus der Vogel-Perspektive.
Das fünfte Bild verdeutlicht, dass der z-Wert der Zylinder-Mitte von G sich als alternierende Summe der
analogen Werte von D, E und F ergibt. Im sechsten Bild sind die Kegel an die Zykel angehängt, bei denen
die Böschungslinien alle mit der xy-Ebene einen Winkel der Größe 45° einschließen. Die letzten vier Bilder
zeigen die gemeinsamen Tangential-Speere von je zwei der Zykeln. Die beiden Tangenten-Speere zu jedem
Zykel-Paar schneiden sich in dessen Ähnlichkeits-Punkt, der Zentrum der Streckungen ist, die ein Zykel des
Paars in den anderen abbildet. Alle sechs Ähnlichkeits-Punkte liegen auf einer Geraden g, die wir Ähnlichkeits-
Achse nennen. g ist Bild der Ursprungsgeraden durch C0 bei der Nullpolarität und liegt darum in der xy-Ebene.
Die Verbindungsgerade von je zwei der Kegelspitzen geht durch einen der Ähnlichkeitspunkte. Einige der
Tangential-Speere sind parallel.

Die Hintereinanderschaltungen der Laguerre-Spiegelungen an D und E stimmen mit denen von G und F überein.
Darum sind die euklidisch gemessenen Tangential-Abstände der Zykeln ZD und ZE, sowie ZF und ZG gleich.
Auch die euklidisch gemessenen Abstände der Kegelspitzen sind gleich. Das Quadrat dieser Abstände ist die
Summe aus dem Quadrat der Abstände der Zykel-Mitten und dem Quadrat der Radius-Differenzen. Dagegen
errechnet man die Tangential-Abstände, indem man diese Summe von Quadraten durch die Differenz ersetzt.
Diese Differenz wird negativ, wenn der eine Zykel ganz im Innern des anderen liegt, so dass es dazu keine reelle
Wurzel gibt, folglich auch keinen Tangentialabstand.

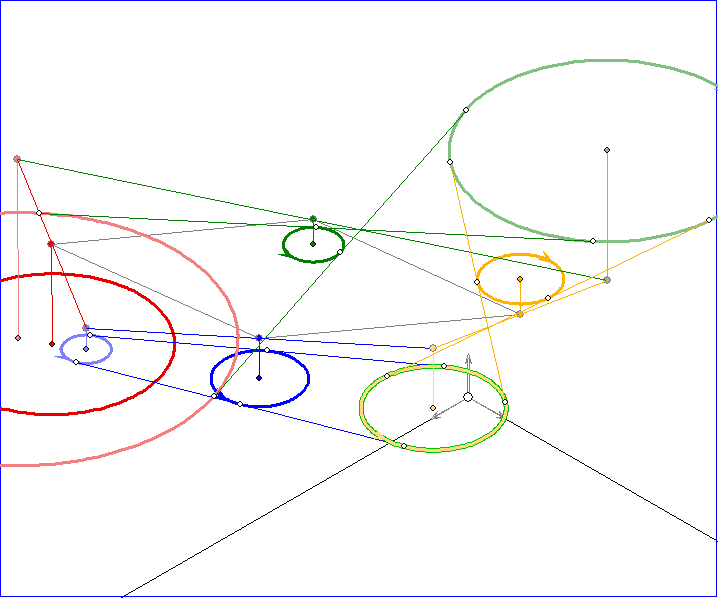
Die Gleitschau zeigt die Hintereinanderschaltung der Laguerre-Spiegelungen an den Zykeln ZD, ZE , ZF
und ZG. Dabei wird der grün-gelben Zykel ZX zunächst an ZD gespiegelt, dann das Bild an ZE , das Bild
davon an ZF. Die letzte Spiegelung an ZG führt dann zurück zu ZX . Der Tangentialabstand des Zykels, an
dem gespiegelt wird, zum Urbild ist stets gleich groß wie der zum Bild. Im ersten Bild der Gleitschau liegt der
Bild-Zykel ZY bei Spiegelung von ZX an ZD ganz im Innern von ZE. Darum ist hier der Tangentialabstand
nicht definiert. Statt der Gleichheit der Tangentialabstände stellt man hier die Gleichheit der Differenz aus dem
Quadrat des Mittelpunkt-Abstands und dem Quadrat der Radien-Differenz fest. Alternativ kann man auch
die Abstände der Kegelspitze zu ZE von den Kegelspitzen zu ZY und der Kegelspitze zum Bild von ZY bei
Spiegelung an ZE betrachten. Diese Abstände sind stets definiert und stimmen bei der Laguerre-Spiegelung
an Zykeln immer überein.