Es lebe die Geometrie!

Erzeugung von gekachelten Wegen mit Hilfe von Nachbar-Bewegungen

Ausgehend von einer Kachel K0 soll mit Hilfe von Bewegungen (Kongruenz-Abbildungen) eine Folge
K1, K2, K3,...von kongruenten Kacheln erzeugt werden, die keine inneren Punkte gemeinsam haben.
Aufeinander folgende Kacheln sollen aber mehr als einen Randpunkt gemeinsam haben, und mit zwei
gemeinsamen Randpunkten sollen auch alle dazwischen liegende Punkte der beiden Randkurven
gemeinsame Punkte sein.

Die Kachel der Folge mit der Nummer n sei mit Kn bezeichnet. Auf dieser Seite wird jede Kachel Kn
um einen von drei Punkten Sn , Hn oder Vn von Kn gedreht, um die nächste Kachel zu erhalten. Diese drei
Punkte haben auf allen Kacheln Kn die entsprechende Lage. Der Betrag des Drehwinkels zur Drehung
um Sn ist bei allen Kachel gleich groß, es sind aber unterschiedliche Drehrichtungen möglich. Bei Hn und
Vn ist der Drehwinkel 180°, an diesen Punkten wird also gespiegelt.

Das erste Bild der Gleitschau zeigt Kacheln K0 (gelb), K1 (grau), K2 (blau) und K3 (gelb) in der
Form eines Schwanenhalses. Bemerkenswert ist dabei, dass K0 und K3 die andern beiden Kachel
ganz umschließen. Ein derartiger Kacheltyp ist zum ersten Mal von Heinz Voderberg 1936 beschrieben
worden. Dabei wurde ein Neuneck wie im zweiten Bild der Gleitschau benutzt. In dem dritten bis
siebenten Bild der Gleitschau wird die Konstruktion des Schwanenhalses erklärt. Man geht von zwei
parallelen Strecken AA' und BB' gleicher Länge im Abstand 1 aus. Der obere Endpunkt der linken
Strecke sei A, der untere der rechten Strecke B. H sei der Mittelpunkt von A und B. Das Lot von A
auf die Strecke BB' trifft deren Mitte, und das Lot von B auf die Strecke AA' trifft auch deren Mitte.
Der Punkt A' wird durch einem Kreisbogen mit H verbunden. Der Bogen zwischen H und B' ist dazu
punktsymmetrisch. Von B aus erscheint die Strecke AA' unter dem Winkel , hier 22,5°. Dreht man
den Kurvenzug AA'HB'B um A mit dem Winkel , so berandet das Drehungsbild zusammen mit dem
Kurvenzug B'HA'A die gelbe Kachel in Form eines Schwanenhalses. Dabei markiert A die Spitze des
Schnabels, die wir bei den Kacheln stets mit S bezeichnen. H gibt die Mitte des hinteren Halsrandes an
und das Drehungsbild V von H die Mitte des vorderen Halsrandes. Durch die Drehung geht die Strecke
BB' in die Basis-Strecke des gelben Schwanenhalses über, die zusammen mit der Schnabelspitze ein
gleichschenkliges Dreieck bildet mit H und V als Schenkelmitten. Beim Schwanenhals ist das Grundmuster
eines gleichschenkligen Dreiecks durch gleichartige Ausbuchtung der Schenkel variiert (siehe das letzte
Bild der Gleitschau). Wenn man Schwanenhals-Kacheln aneinanderlegt, kann die Basis-Strecke einer
Kachel auf eine Schnabel-Strecke einer Nachbar-Kachel treffen. Wenn man jede Schwanenhals-Kacheln
durch ein gleichschenkliges Dreieck ersetzt, kommt es darum zu Überlappungen.

Eine Kurve in der Form der Kurve AA'HB'B bezeichnen wir im Folgenden als 'Z-Kurve'. Wenn
man AA'HB'B um B mit dem Winkel dreht, ergibt das Bild zusammen mit A'HB'B die graue
Schwanenhals-Kachel, bei der die Schnabelspitze S der Punkt B ist.

Die Zeichnungen der Gleitschau machen deutlich, dass der Mittelpunkt des Bogens A'H nur in einem
eingeschränkten Intervall der Mittelsenkrechten von A'H liegen kann, wenn sich die Randkurve von K0
nicht selbst überschneiden soll.

Die Kachel K1 entsteht aus K0 durch Drehung gegen den Uhrzeigersinn um die Schnabelspitze S0 von K0
mit dem Drehwinkel 22,5°. Dabei wird die hintere Halsmitte H0 von K0 in den Punkt H1 abgebildet, der
in K1 dem Punkt H0 von K0 entspricht. Durch Drehung von H1 um die Schnabelspitze von K1 um 22,5°
ergibt sich die vordere Halsmitte V1. Die Kachel K2 ensteht durch Drehung um V1 mit dem Winkel 180°.
Dabei wird die Schnabelspitze S1 von K1 in die Schnabelspitze S2 von K2 abgebildet. Dreht man K2
um S2 mit dem Winkel -22,5°, also im Uhrzeigersinn, so erhält man K3. Wir beschreiben diese Folge mit
Hilfe des 'Konstruktionsterms' .

Die Gleitschau zeigt den Aufbau eines geschlossenen Kachelwegs aus Schwanenhals-Kacheln zum
Winkel , bei dem die jeweils folgende Kachel durch eine Drehung aus der vorhergehenden
entsteht. Die Drehung gegen den Uhrzeigersinn um die Schnabelspitze S mit dem Winkel wird ebenfalls
mit S bezeichnet und die Drehung um (also im Uhrzeigersinn) mit . Die Drehungen um 180° um
die hintere bzw. vordere Hals-Mitte werden wie die Drehpunkte selbst mit H bzw. V bezeichnet. Die
Reihenfolge der Abbildungen ist am unteren Rand der Animation festgehalten. Der jeweils letzte Buchstabe
gibt die aktuell durchgeführte Drehung an.

Der Konstruktionsterm des ersten Kachelwegs der Animation ist . Ausgehend von einer
bereits gelegten Ausgangskachel K0 ergibt sich hieraus eindeutig der ganze Weg, wenn man die Klammern
und die Hochzahlen nach den Regeln der Algebra auflöst, den neuen Term von links nach rechts sukzessive
aufschreibt und dann den jeweils zuletzt geschriebenen Buchstaben des Teil-Terms auf die letzte bereits
gelegte Kachel bezieht. Zum Beispiel der zweite Teil-Term SV legt die die erste blaue Kachel K2 fest.
Neben der Bedeutung als Konstruktions-Term hat SV für K2 noch einen weiteren Sinn. Dazu deutet
man die Buchstaben S und V beide als Drehungen um die Punkte S0 und V0 bei der Ausgangs-Kachel
K0. Dann ist . (Die Reihenfolge der Abbildungen ergibt sich hier beim
Lesen des Abbildungs-Terms von rechts nach links. ) ist eine gerade Bewegung, dessen
Drehwinkel die Summe der Drehwinkel von S, V und ist, also . Darum ist
die 180°-Drehung um V1. Es folgt . Analog zeigt
man und , und so weiter. Bei einer Deutung der Buchstaben des
Konstruktionsterms als Drehungen um Punkte von K0 ist also Kn das Bild bei der Abbildung, die
durch Hintereinanderschaltung dieser Drehungen von rechts nach links entsteht. Da der letzte Term
des ersten Kachelwegs wieder zur Ausgangskachel K0 führt, muss der Term (als
Abbildung verstanden) die identische Abbildung beschreiben.

Der zweite Kachelweg hat den Konstruktionsterm . Die Ausgangskachel dieses Wegs
erhält man, wenn man K0 des ersten Wegs so verschiebt, dass die verschobene Kachel an die Randstrecke
am Kopf von K3 anschließt.

Zur Konstruktion von bestimmten Kachelwegen ist es sinnvoll, sich am gewünschten linken oder rechten
Wegrand zu orientieren. Zur Beschreibung der Konstruktionsregeln gehen wir davon aus, dass die
Ausgangskachel mit der Schnabelspitze am linken Rand in Richtung des Wegs zeigt. Wenn sich dann
eine folgende Kachel mit dem Kopf den rechten bzw. linken Rand berührt, zeigt der Schnabel gegen bzw.
in Wegrichtung. Die Fortsetzungsregeln hängen davon ab, ob die Randstrecke des letzten Kachel zum
Kopf (K) oder zur Basis (B) dieser Kachel gehört.

Für den linken Rand gilt:

Wenn die letzte Strecke vom Typ (K) ist, entsteht eine neue Randstrecke vom Typ (B) bzw. (K) in
geradliniger Fortsezung durch Anfügen des Terms bzw. . Die neue Randstrecke ist dagegen
um das k-fache des Winkels nach links gedreht (mit natüllichem k), wenn man oder
nsetzt. Eine nach rechts gedrehte Strecke kann am linken Rand keine (K)-Strecke fortsetzen. Wenn die
letzte Strecke am linken Rand vom Typ (B) ist, gibt es nur eine Fortsetzung nach rechts und zwar durch
den Term oder , der zu einer um gedrehten Strecke vom Typ (B) bzw. (K) führt.

Die Animation verdeutlich eine weitere Möglichkeit, einen Kachelweg zu konstruieren, der der vom
Ansetzen von Kachel unterscheidet. Man geht von der oben definierten Z-Kurve AA'HB'B aus und
bildet diese Kurve Z0 mit einer Folge Zn von Kongruenzabbildungen ab. Zu Z1 kommt man durch
Drehung von Z0 um A mit dem Drehwinkel oder um B mit dem Drehwinkel . Um den Bezug zu
Z0 zu verdeutlichen, nennen wir A bzw. B auch A0 bzw. B0. Die auf Zn folgende Kurve entsteht durch
Drehung um den Endpunkt An bzw. Bn von Zn ebenfalls mit dem Winkel bzw. . Im Term der
Konstruktion bezeichnen wir unter Missbrauch der Sprache diese Drehungen ebenfalls mit A bzw. B,
da die Nummer der Abbildung sich aus der Stellung im Term ergibt.

Zwei aufeinander folgende Z-Kurven bestimmen den Rand einer Schwanenhals-Kachel. Dazu setzt
man die Kurve Zn von An bis Bn mit der Kurve Z(n+1) in umgekehrter Richtung von B(n+1) bis
A(n+1) fort, wobei Bn und B(n+1) sowie A(n+1) und An geradlinig verbunden werden . Die Strecke,
die dabei zweimal durchlaufen wird (in entgegengesetzter Richtung), wird anschließend gelöscht.

Der Konstruktionsterm der Kachel-Folge ergibt sich aus dem der Z-Kurven folgendermaßen:

Die Folge der Buchstaben A und B beginne mit A. Wenn der zweite Buchstabe ein A bzw. B ist, wird
der erste Buchstabe des Kachel-Terms S bzw. V. Analog verfährt man mit dem zweiten Buchstaben
des Kachel-Terms, wenn der zweite Buchstabe des Z-Kurven-Terms A ist. Wenn er B ist, wird der
zweite Buchstabe des Kachel-Terms bzw. , je nachdem der dritte Buchstabe des Z-Kurven-
Terms A oder B ist. Das Paar der Buchstaben an der n-ten und (n+1)-ten Stelle des Z-Kurven-Terms
bestimmt entsprechend den n-ten Buchstaben des Kachel-Terms. Kurz:

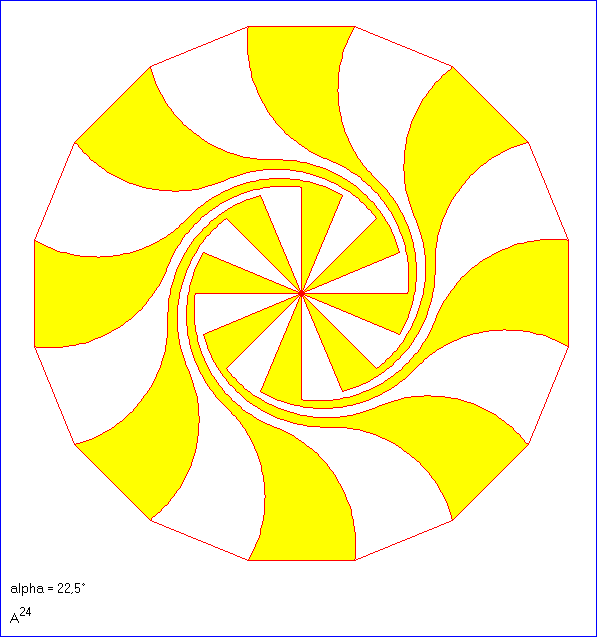
Die Gleitschau zeigt Beispiele für durch Z-Kurven-Terme bestimmte geschlossene Kachelwege.

Hier wird eine punktsymmetrische Spirale aus zwei Schwanenhals-Kachelwegen aufgebaut, die bei einer
Fortsetzung ins Unendliche die ganze Ebene ausfüllt. Für werden beim Konstruktionsterm
des ersten Kachelwegs Terme für n = 0, 1, 2, ... hintereinandergesetzt und bei der Z-Kurve
Terme der Form . Für mit natürlicher Zahl k > 8 wird die Hochzahl 8 durch k ersetzt.
Die Hochzahl n ist an Hand der Länge der Strecken am rechten Rand des Wegs erkennbar. Diese ist
nämlich das (n+1)-fache der Länge der beiden Strecken AA' und BB' an den Enden der Z-Kurve.

Der zweite Weg setzt bei einer Ausgangskachel an, die durch Spiegelung der Ausgangskachel des ersten
Wegs an dessen Punkt H0 entsteht. Während der erste Weg nach oben startet, beginnt der zweite nach
unten. Der Konstruktionterm des zweiten Wegs ergibt sich durch Vertauschung der Rollen von A und B
beim Konstruktionsterm des ersten Wegs.

Die Gleitschau zeigt die Füllung der Ebene mit m = 2, 3, 4 oder 5 Spiralwegen, die sich jeweils aus zwei
Kachelwegen zusammensetzten. Diese Wege haben wie bei m = 1 einen Konstruktionsterm, der sich
aus Termen der Form bzw. zusammensetzt. Hier durchläuft aber n nicht die
natürlichen Zahlen i = 0, 1, 2, 3,..., sondern die Werte einer arithmetische Folge der Form
mit einer natürlichen Zahl j, die für m = 1 Null ist. Bei der ersten Spirale zu m = 2 hat der nach oben
startende Weg den j-Wert 0 und der nach unten startende den j-Wert 1. Die Startkacheln der zweiten
Spirale ergeben sich aus denen der ersten durch Verschiebung mit dem Vektor . Der j-Wert beim
nach oben startenden Weg ist hier 1, der beim nach unten beginnenden Weg 0. Für m = 3 sind die Paare
der j-Werte (0 ; 2), (1 ; 1) und (2 ; 1). Allgemein sind es Paare natürlicher Zahlen mit der Summe .