Es lebe die Geometrie!

Andere Sterne

Bandwerke, die mit durch Seitenspiegelungen erzeugte Kachelungen konstruiert werden, sind meist
von sternförmige Figuren geprägt. Die Anzahl der Spitzen beträgt dabei häufig 3, 4, 6, 8 oder 12. Dies
ergibt sich daraus, dass die Kacheln nur Innenwinkel der Größe 30°, 45°, 60° und 90° haben können,
wenn man als Nachbarbewegungen ausschließlich Achsenspiegelungen zulässt. Bei der Verwendung von
Bandwerken für dekorative Zwecke, zum Beispiel an Moscheen, wurde es deshalb als Herausforderung
angesehen, Konstruktionen mit anderen Anzahlen von Stern-Spitzen zu finden, insbesondere mit den
Anzahlen 9 oder 5. Die folgenden Gleitschauen zeigen Beispiele für derartige Konstruktionen. Wir
verwenden auch hier Billard-Pfade. Dabei ist es sinnvoll, innere Spiegelungen und Reflexionen nur an
Strecken zuzulassen, Kreise also auszuschließen, weil dann Verrückungen des Startpunktes mit
festgehaltenem Startwinkel bei allen Strecken des Pfads lediglich zu Verschiebungen führen.

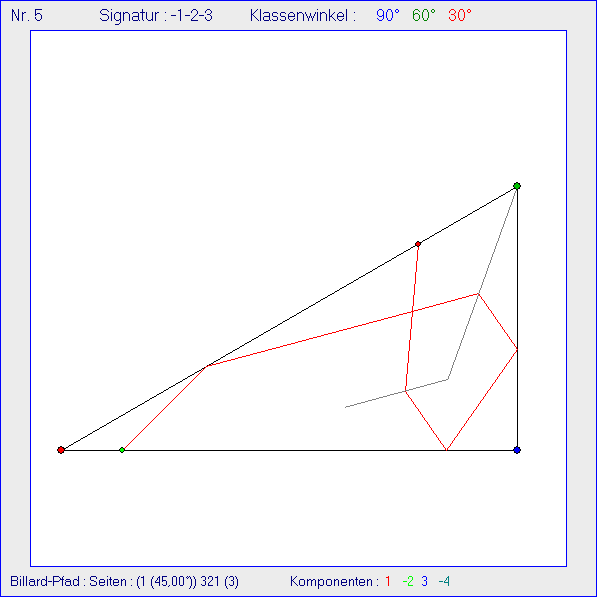
Das Bandwerk mit dem 30°-90°-60°-Ausgangsdreieck zeigt 9-Sternen an den grünen Eckpunkten
mit dem Innenwinkel 60°. Dazu muss der Billard-Pfad im Ausgangsdreieck an der grünen Ecke C drei
Stern-Seiten erzeugen. Diese Seiten sollen also gleich lang und entsprechende Endpunkte der Seiten
gleich weit von C entfernt sein. Eine 'Drittelungs-Gerade' durch C, die mit BC oder AC einen Winkel der
Größe 20° einschließt, muss deshalb Symmetrie-Achse des 9-Sterns sein. Darum wird hier die grau
gezeichnete Spiegelungs-Strecke S1 mit dem Anfangspunkt C und dem Richtungswinkel 250° benutzt,
die den Winkel bei C drittelt. Die zweite Spiegelungs-Strecke S2 setzt am Schnittpunkt der Drittelungs-
Geraden mit der Winkelhalbierenden zu B an und kann verschieden Richtungswinkel haben, in der
Gleitschau z. B. 195°, 190° und 205°. In allen drei Fällen ist es möglich, durch geeignete Wahl des Start-
Punktes und des Start-Winkels einen regelmäßigen 9-Stern zu erzeugen. Um dies zu verstehen, ist es
sinnvoll, die Richtungswinkel der Strecken des Billard-Pfads zu betrachten. Der Richtungswinkel von
S2 sei a genannt und der Richtungswinkel der ersten Pfad-Seite . Für die folgenden Richtungswinkel
gilt dann:





Damit ein regelmäßiger 9-Stern zustande kommen kann, muss für den Richtungswinkel 230° der zweiten
Drittelungs-Geraden durch C gelten: . Daraus folgt . Darum sind
die Startwinkel der Gleitschau 45°, 40° und 55°. Dass die Seiten des 9-Sterns gleich lang sind, erreicht
man durch geeignete Verschiebung des Startpunktes auf AB. Beim Startwinkel 55° ergibt sich zusätzlich
die Regelmäßigkeit, dass die dritte Pfad-Strecke rechtwinklig in die vierte abknickt.

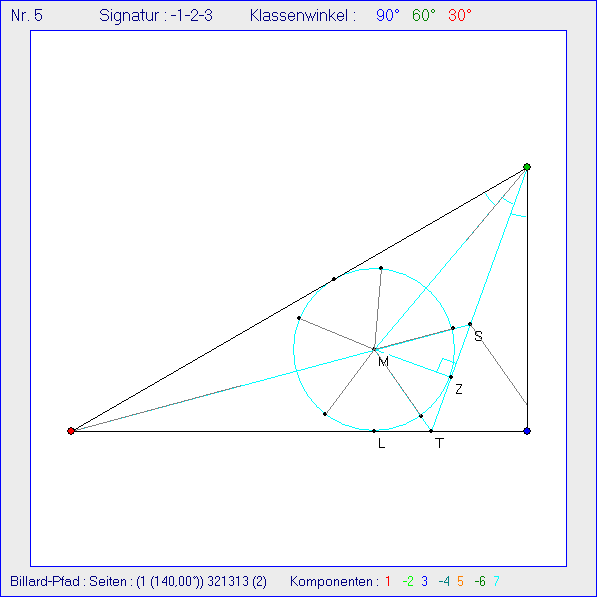
Die Gleitschau zeigt im 30°-60°-90°-Ausgangsdreieck ein Beispiel für die Erzeugung eines 5-Sterns und eines
9-Sterns mit Hilfe eines Billard-Pfads. Dafür werden acht graue Strecken mit inneren Spiegelungen benutzt, die
wir mit S1 bis S8 bezeichnen. S1 bis S5 (gegen den Uhrzeigersinn nummeriert) haben als Anfangspunkt den
schwarz markierten Schnittpunkt M der Winkelhalbierenden g durch A und der Geraden h durch C, die mit
AC einen Winkel der Größe 20° einschließt, also Drittelungsgerade durch C ist. Die Richtungswinkel von S1
bis S5 gegenüber der Rechtsachse sind 15°, 85°, 157,5°, 232,5° und 305°. Der Anfangpunkt von S6 ist der
ebenfalls schwarz markierte Schnittpunkt S von g mit der zweiten Drittelungsgeraden j durch C, und der
Richtungswinkel beträgt wie bei S5 305°. Die Strecken S7 bzw. S8 haben C bzw. A als Anfangspunkt und
die Richtugswinkel 230° bzw. 15°, liegen also auf h bzw. g.

Der schwarze Schnittpunkt von j mit der Seitengeraden AB sei T genannt. Die hellblau markierten Strecken
verdeutlichen, dass M der Inkreis-Mittelpunkt in dem Dreieck ATC ist. Dabei bilden die Punkte M, S und T
ein gleichschenkliges Dreieck mit der Spitze in M und den Innenwinkeln 70°, 55° und 55°. Der Mittelpunkt
von ST sei Z gennant. Z ist Berührpunkt des Inkreises von ATC mit j. Die Länge der Strecke MZ ist also der
Radius r des Inkreises von ATC.

Der Billard-Pfad startet in den ersten sieben Bildern der Gleitschau mit dem Richtungswinkel 140° in dem Punkt
auf AB, für den die erste Strecke des Billard-Pfads Z trifft. Dann gilt . In den folgenden
Bildern wird bei unverändertem Richtungswinkel der Ort des Startpunkts verändert, um zu zeigen, dass dann die
Pfad-Strecken nur parallel verschoben werden.

Das Ziel bei der Wahl der Richtungswinkel bestand darin, einen möglichst regelmäßigen 5-Stern zu erzeugen, so
dass die Begleit-Figuren ebenfalls Regelmäßigkeiten zeigen und untereinander möglichst kongruent sind. Inwieweit
dies erreicht wurde, ergibt sich zunächst aus der Folge der Richtungswinkel des Billard-Pfads, nämlich:

(parallel zu j)


(entgegengesetzt zu )
(parallel zu AB)
( wie )







(parallel zu AC)

Alle Strecken (von Knickpunkt zu Knickpunkt) des Billard-Pfades mit Ausnahme der 3., 4. und 5. haben
also einen Partner, dessen Gegenrichtung sich durch Spiegelung an g ergibt. Die Hintereinanderschaltung der
Spiegelung an AC, der Spiegelung an h und der Spiegelung an BC stimmt mit der Spiegelung an j überein.
Da die Hintereinanderschaltung der Reflexion an AC, der Spiegelung an S7 und der Reflexion an BC die
2. Strecke des Billard-Pfads in die 5. überführt, sind diese beiden Strecken nicht nur parallel zu j, sondern
haben auch den gleichen Abstand von j. Der Schnittpunkt der 1. und 6. Strecke liegt darum auf j, da j
Winkelhalbierende der Geraden zu S1 und S6 ist. Dies gilt für alle Startpunkt des Pfads.

In den ersten Bildern der Gleitschau wurde der Startpunkt so gewählt, dass die erste Pfad-Strecke durch
Z geht. Wegen der Symmetrie zu g ist der Schnittpunkt der 2. und der letzten Strecke dann der kleine rote
Punkt auf h, der sich aus Z durch Spiegelung an g ergibt. Dann bilden diese beiden Strecken mit j und AC
eine Raute. Folglich geht durch den kleinen roten Punkt auf j nicht nur die letzte Strecke des Pfads, sondern
auch die vierte. Dieser Punkt ist die Spitze eines von Pfad-Strecken gebildeten zu j symmetrischen Sechsecks
mit den Innenwinkeln 80°, 140°, 110, 140°, 110° und 140°.

Eine Seite dieses Sechsecks ist Schenkel zur Spitze Z im zentralen 5-Stern. Sie teilt im Dreieck MZS
ein gleichschenkliges Dreieck ab. Daraus errechnet man ihre Länge zu . Der zugehörige
zweite Schenkel im 5-Stern zu Z ist gleich lang, weil MSZ aus MTZ durch Spiegelung an MZ entsteht.
L sei der Fußpunkt des Lots von M auf AB. Dann sind die Innenwinkel von MTL gleich groß wie die
von MTZ, und folglich L auch Spitze des 5-Sterns mit einem Schenkel von gleicher Länge wie bei Z.
L und Z sind Eckpunkte einer Figur, die kongruent zu einer Hälfte des oben erwähnten Sechsecks ist.
Da ML den von den Strecken S4 und S5 gebildeten Winkel von 72,5° nicht teilt, sind die Schenkel der
Spitze L im 5-Stern verschieden lang. Da S4 aber den Winkel AML halbiert, hat auch die Spitze auf g
den gleichen Abstand von M wie L und Z. Wegen der Symmetrie zu g liegen darum alle Spitzen auf
dem Inkreis von ATC.

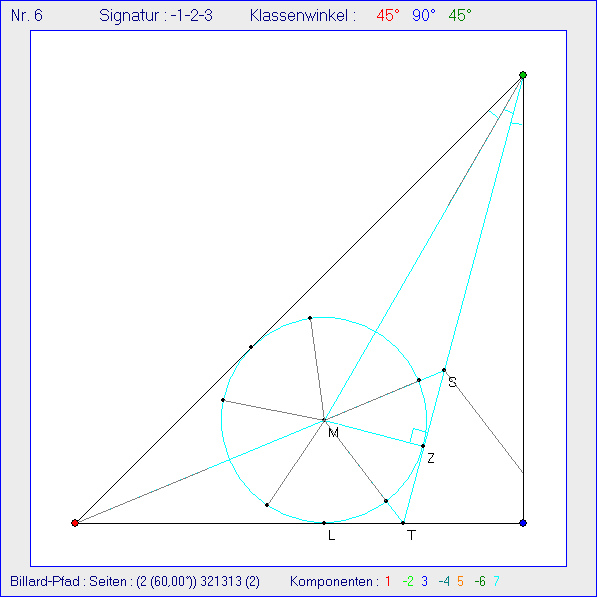
Die Konstruktion der vorherigen Gleitschau kann analog auch in einem Ausgangsdreieck mit den
Innenwinkeln 45°, 90° und 45° durchgeführt werden. Die Strecken S1 bis S8 haben dann die
Richtungswinkel 22,5°, 97,5°, 168,75°, 236,25°, 307,5°, 307,5°, 240° und 22,5°. In den ersten
drei Bildern der Gleitschau startet der Billard-Pfad auf der Seite BC mit dem Richtungswinkel 150°.
Dann trifft die erste Strecke des Pfads den Punkt Z auf der Drittelungs-Geraden j. Es ergibt sich
auch hier ein 5-Stern mit Spitzen auf dem Inkreis von ABC . Außerdem ist Z Eckpunkt eines zu j
symmetrischen Sechsecks, das zudem zwei parallele Seiten hat. In den folgenden dreißig Bildern der
Gleitschau wird der Startwinkel des Billard-Pfads variiert, aber der Startpunkt dabei so gewählt,
dass Z weiterhin auf der ersten Billard-Strecke liegt. Es ergeben sich dabei Bandwerke mit
entsprechenden Regelmäßigkeiten mit Ausnahme der genannten Parallelität.

In den letzten vierzehn Bilder der Gleitschau haben die Innenwinkel des Ausgangsdreiecks wie in den
ersten beiden Gleitschauen die Größen 30°, 90° und 60°, aber hier wird der 30°-Winkel bei A gedrittelt.

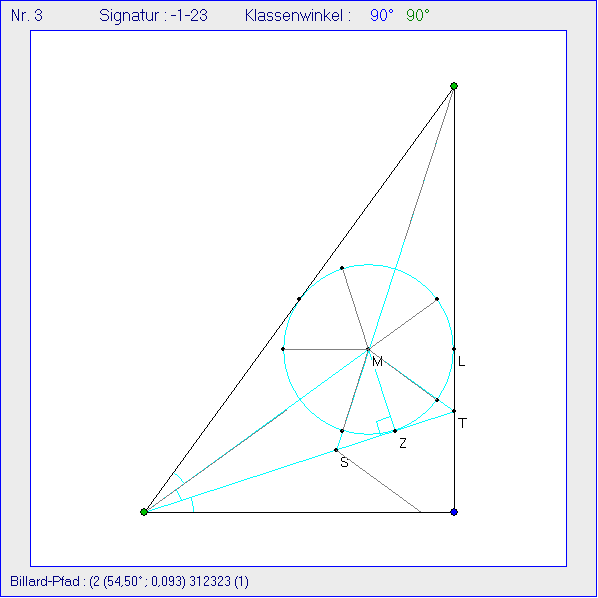
Das Ausgangsdreieck hat hier die Innenwinkel 54°, 90° und 36°. Eine Kachelung mit der Signatur
-1-2-3, bei der alle Nachbar-Bewegungen Achsenspiegelungen sind, ist damit nicht möglich. Darum
wird für die Seite 3 die Achsenspiegelung durch eine Punktspiegelung am Seiten-Mittelpunkt ersetzt.
Ein Bandwerk ergibt sich dann aber nur, wenn die Menge der Treffpunkte des Billard-Pfads auf
Seite 3 (= AC) punktsymmetrisch zum Mittelpunkt ist. Das ist bei diesem Dreieck und der Methode
der beiden vorangehenden Gleitschauen nur bei Drittelung des Winkels von 54° der Fall (nicht beim
Winkel von 36°). Dann ist der erzeugte 5-Stern regelmäßig, sofern die erste Strecke des Billard-Pfads
den Punkt Z trifft.

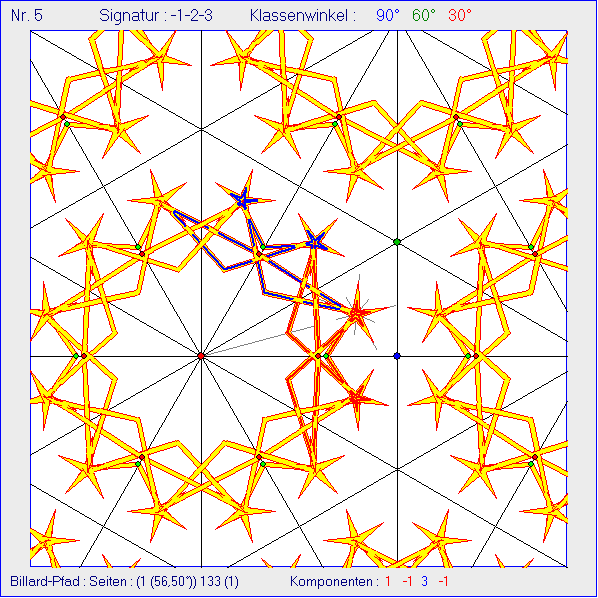
In dieser Gleitschau wurden die 5-Sterne Hilfe von vier kurzen und fünf langen Spiegelungs-Strecken
mit dem Anfangspunkt im Inkreis-Mittelpunkt M und einer Strecke auf der Winkelhalbierenden durch A
erzeugt. Die Winkel zwischen benachbarten Strecken bei M betragen 36° mit einer Ausnahme bei zwei
aufeinanderfolgenden kurzen Strecken, die einen Winkel von 72° bilden. Jeder Billard-Pfad hat drei
Reflexionen an Seiten.

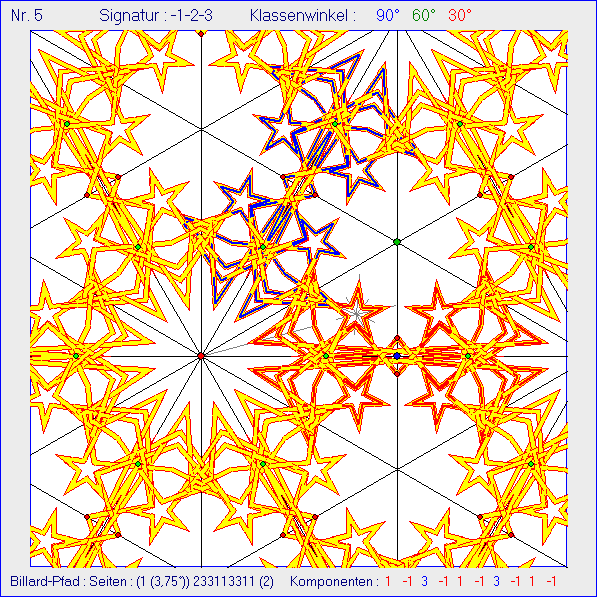
Unter den gleichen Spiegelungs-Bedingungen wie in der vorhergehenden Gleitschau werden Billard-Pfade
mit neun Reflexionen an Seiten benutzt.