Es lebe die Geometrie!

Pole und Berührpunkte beim Billard in der Ellipse

Der blaue Sehnenzug innerhalb der roten Ellipse stellt die Bahnkurve (Trajektorie) einer punktförmigen
Billard-Kugel dar, die in Richtung des roten Pfeils abgeschossen wird und beim Auftreffen auf die Ellipse
so reflektiert wird, dass der Winkel der Sehne mit der Tangente im Auftreffpunkt vor und nach der
Reflexion gleich ist. Die hellblauen Punkte sind die Pole der Sehnen, also die Schnittpunkte der Tangenten
in den beiden Sehnen-Endpunkten auf der Ellipse. Die dunkelblauen Punkte sind die Fußpunkte der Lote
von den Polen auf die zugehörigen Sehnen. Die Pole und die Lotfußpunkte liegen auf zwei Ellipsen, wobei
die Sehnen die Lotfußpunkt-Ellipse in den Lotfußpunkten tangential berühren. Dies ist immer dann der Fall,
wenn die erste Sehnen nicht die Strecke zwischen den beiden roten Ellipsen-Brennpunkten kreuzt. (Das
wird im Folgenden begründet.) Die Brennpunkte der Lotfußpunkt-Ellipse stimmen mit denen der roten
Ellipse überein, nicht aber die der Pol-Ellipse.

Wenn die erste Sehne der Billard-Trajektorie einen Brennpunkt trifft, dann gilt dies auch für
alle folgenden Sehnen. Die hellblauen Pole der Sehnen liegen auf den Polaren der beiden
roten Brennpunkte.

Hier kreuzt die erste blaue Sehne das Innere der Strecke zwischen den roten Ellipsen-Brennpunkten.
Dann liegen die hellblauen Pole und die dunkelblauen Lotfußpunkte nicht auf Ellipsen, sondern auf
Hyperbeln, wobei die Lotfußpunkt-Hyperbel die gleichen Brennpunkte hat wie die Billard-Ellipse.

Die beiden Bilder sollen zeigen, dass die zwei blauen Sehnen der roten Ellipse, die durch Reflexion
auseinander hervorgehen, beide Tangenten der gleichen (blau gezeichneten) Ellipse bzw. Hyperbel sind,
wobei deren Brennpunkte mit denen der roten Ellipse übereinstimmen.
Wir gehen dabei von folgender definierenden Eigenschaft einer Ellipse bzw. Hyperbel mit den
Brennpunkten B1 und B2 aus: Sie ist nämlich der geometrische Ort der Punkte P, für welche die
Summe bzw. Differenz der Abstände von B1 und B2 konstant ist; diese Zahl r ist dann die Länge
der größten Sehne bzw. kleinsten Sehne mit Endpunkten auf verschiedenen Hyperbel-Ästen. Die
definierende Eigenschaft hat folgende Konsequenzen:
Eine der beiden Winkelhalbierenden der Geraden B1P und B2P ist Tangente der Ellipse bzw. Hyperbel.
Und wenn man B2 an der Tangente spiegelt, erhält man einen Punkt S2, der auf einem Kreis um B1 mit
dem Radius r liegt.
Um zu zeigen, dass die blauen Sehnengeraden g und g' der roten Ellipse Tangenten derselben blauen Ellipse
bzw. Hyperbel sind, muss darum gezeigt werden, dass in den Zeichnungen die beiden grünen Punkte S2 und
S2' vom rechten Brennpunkt B1 den gleichen Abstand haben. Dazu sei h2 die Verbindungsgerade von B2
mit dem Schnittpunkt von g und g'. Wir betrachten die Hintereinanderschaltung der Spiegelungen an g, h2
und g'. Sie bildet S2 in S2' ab. Andererseits ist dies eine Hintereinanderschaltung von drei Spiegelungen an
Geraden mit einem gemeinsamen Punkt und stimmt darum mit einer einzigen Spiegelung an einer Geraden
durch diesen Punkt überein, und zwar an der Geraden, die mit g' einen gleich großen Winkel einschließt wie
g mit h2. Diese Gerade muss darum die Verbindungsgerade h1 von B1 mit dem blauen Reflexionspunkt sein,
in dem sich g, h2 und g' schneiden. Die Spiegelung von S2 an h1 ergibt folglich S2'. Darum haben S2 und
S2' von B1 den gleichen Abstand.

In den Animationen wurde dargestellt, dass die blauen Berührpunkte der Sehnen einer Billard-Bahnkurve
Lotfußpunkte zu den Polen der Sehnen sind. Das soll in folgendem Satz bewiesen werden.
Satz : Zu einer Ellipse E mit der Gleichung sei ein Kegelschnitt (Ellipse oder Hyperbel)
K mit der Gleichung gegeben, der die gleichen Brennpunkte wie E hat. Q mit den Koordinaten
sei ein Punkt auf K. Dann ist der Punkt P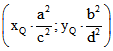 der Pol der Tangente in K bezüglich
E und Q ist der Fußpunkt des Lots von P auf die Tangente. P liegt auf dem Kegelschnitt mit der Gleichung
.
Beweis: Wegen der Gleichheit der Brennpunkte von E und K ist mit dem Minus- oder
Plus-Zeichen vor d, je nachdem K eine Ellipse oder Hyperbel ist. Die Tangente g in Q hat die Gleichung
. Die Polare eines Punktes Pbezüglich der Ellipse E hat die Gleichung
. Wenn diese Polare mit g übereinstimmt, muss P der Punkt 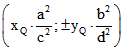sein.
Die Senkrechte der Tangente in Q hat die Gleichung . Die Einsetzung
der Koordinaten von P ergibt die Gleichung , die wegen der Gleichheit
der Brennpunkte wahr ist. Darum ist Q der Fußpunkt des Lots von P.