Es lebe die Geometrie!

Das sRGB-Parallelepiped

Der hier gezeichnete Spat (Parallelepiped) stellt eine Zuordnung der beim Computer meist benutzten
sRGB-Farben (standard-Red-Green-Blue) zu Punkten des dreidimensionalen Raums her. Dabei wird
ein Koordinatensystem zugrundegelegt, das auf einer Konvention berüht, die von der Internationalen
Beleuchtungskommission CIE festgelegt wurde. Der Spat wird in diesem Koordinatensystem von den
Vektoren , und
aufgespannt. Dies sind die Ortsvektoren der Punkte von drei
Grundfarben der additiven Farbmischung. Sie werden in der Zeichnung als graue Pfeile gezeichnet, die
den Schwarz-Punkt S(0 ; 0 ; 0) mit dem Rot-Punkt R, dem Grün-Punkt G und dem Blau-Punkt B an den
Ecken des Spats verbinden. Die übrigen Eckpunkte sind der Cyan-Punkt C, der Magenta-Punkt M, der
Gelb-Punkt Y und der Weiß-Punkt W. Die zugehörigen Ortsvektoren sind , ,
und . Physikalisch realisiert werden nur Licht-Flecken in den Farben auf den
Verbindungsstrecken von S mit R, G und B. Sie erzeugen in Auge des normalen Betrachters einen Farbeindruck
wie bei Mischungen von Rot, Grün und Blau mit Schwarz. Dass alle Farben im Spat vom Auge wahrgenommen
werden, beruht auf der Verarbeitung der Impulse, die die Photonen in den drei Zapfen-Arten des Auges
auslösen, wenn diese Licht-Flecken dicht nebeneinander liegen. Drei kleine Licht-Flecken zu Punkten auf den
Strecken SR, SG und SB mit den Ortsvektoren , und erzeugen im Auge des
normalen Betrachters einen Farbeindruck, der durch den Punkt beschrieben wird, dessen Ortsvektor
ist. Dies ist die Aussage eines Naturgesetzes, das der Mathematiker Hermann Grassmann
(1809-1877) im Rahmen der auch von ihm erfundenen Vektorrechnung formuliert hat (Grassmannsches Gesetz).
Eine Bestätigung findet dieses Gesetz durch Experimente, bei denen Beobachter beurteilen, wann zwei farbig
beleuchtete Flächen in ihrer Wahrnehmung denselben Farbeindruck (Farbvalenz) erzeugen. Dabei durchläuft die
Farbe der ersten Fläche alle überhaupt erzeugbaren Farben, während die Farbe der zweiten Fläche dadurch
zustande kommt, dass diese Fläche mit rotem, grünem und blauem Licht bestimmter Farbart, aber unterschiedlicher
Intensität beleuchtet wird. Durch Variation der Intensitäten kann für viele die Gleichheit mit erreicht werden.
Dies sind die Farben, die zu den Punkten des sRGB-Spats gehören, wenn man die drei Farbarten von R, G und
B benutzt. Es gibt aber Farben , für die auf diese Weise nicht erreichbar ist. Erst wenn man die erste
Fläche zusätzlich zum Licht der Farbe mit einer der Farben von R, G oder B beleuchtet, z. B. von R, kann
man man Übereinstimmung mit erreichen, wobei dann die zweite Fläche nur noch mit den Farben von G und
B beleuchtet werden muss. Wenn die Farbvalenz von zum Vektor gehört, dann gibt es für diese Farbe
nicht-negative Vorzahlen r, g und b mit , so dass gilt. Diese
Farbe ist dann aber auf einem Monitor, der den sRGB-Farbraum benutzt, nicht darstellbar.

Die Ortsvektormenge des Spats ist dagegen . Zur Festlegung der
Vorzahlen r, g und b benutzt man eine Funktion 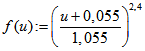, wobei 2,4 als 'Gammawert' bezeichnet
wird. Da der Graph dieser Funktion nicht durch den Ursprung geht, ersetzt man ihn für kleine Werte von u durch
die Ursprungsgerade, die Tangente an f ist, und zwar in dem Bereich vom Ursprung bis zum Tangentenberührpunkt.
Bei der 8-Bit-TIFF-Bildspeicherung werden für die Vorzahlen r, g und b werden nur die Zahlen mit
ganzzahligem i im Bereich genutzt. Den Tripeln sind
dann eineindeutig die ganzen Zahlen zwischen 0 und zugeordnet. Zu den Farbpunkten
S, R, G, B, C, M, Y und W gehören darum die Zahlen 0, 255, , , ,
, und . Im Sedezimalsystem (Hexadezimal=
system) mit der Basis 16 statt 10 und den Zeichen '0', '1', '2',...,'9', 'A', 'B', 'C', 'D', 'E', 'F' für die Ziffern 0 bis 15
sind dies die Zahlen, die sich mit höchstens sechs Zeichen darstellen lassen. Dabei werden Zeichenketten mit weniger
als sechs Zeichen nach links durch Nullen zu sechs Zeichen ergänzt. Die Farbpunkte S, R, G, B, C, M , Y und W
werden also durch die Sedezimalzahlen 000000, 0000FF, 00FF00, FFFF00, FF00FF , 00FFFF und FFFFFF
beschrieben. (Siehe dazu Simon, K., Farbe im digitalen Publizieren, Springer-Verlag 2008.)

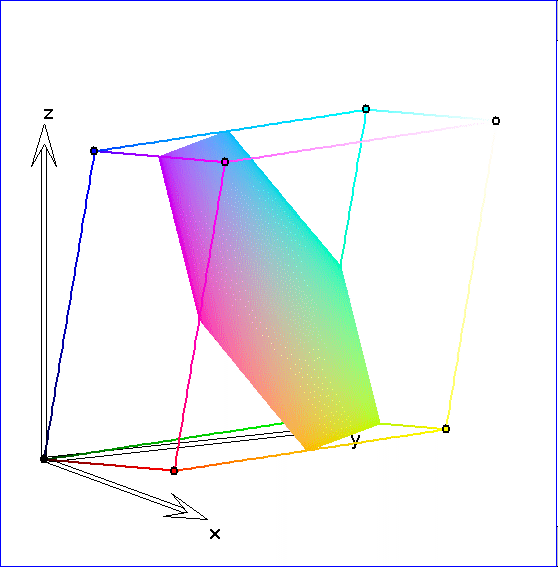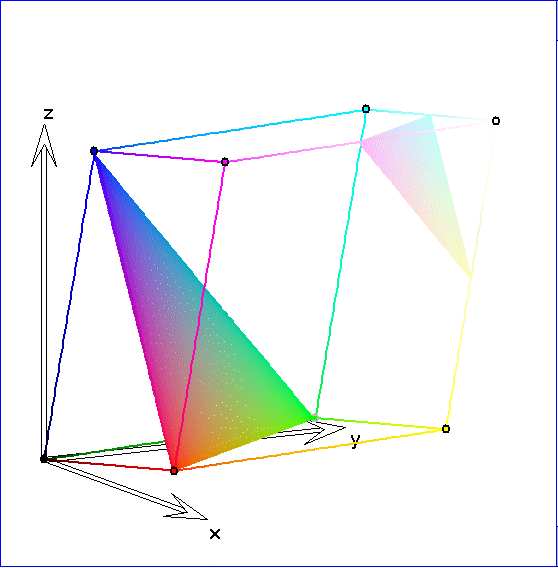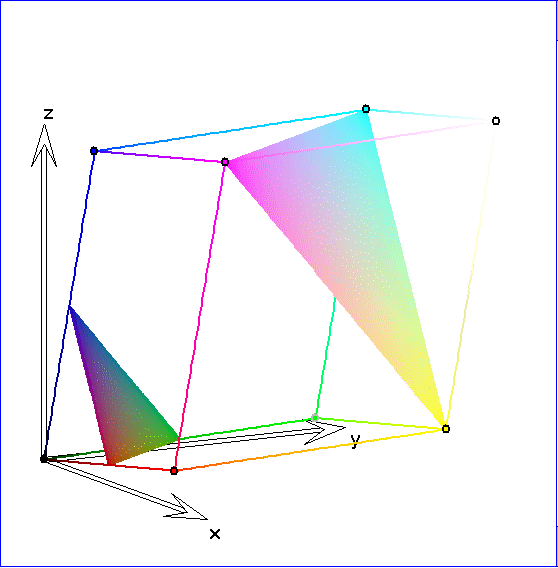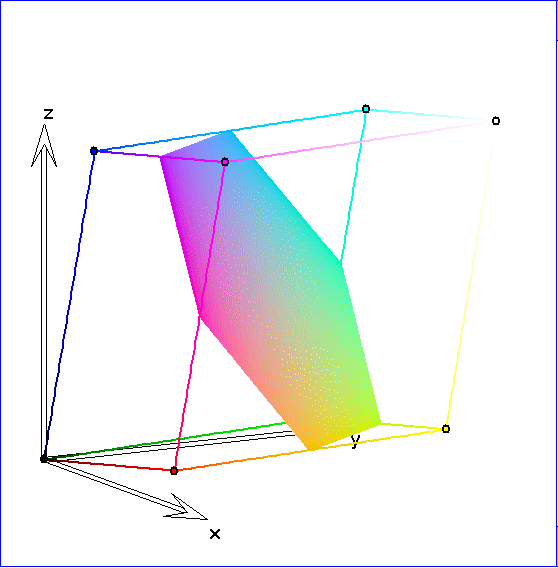
Hier werden die Farbpunkte des Spats dargestellt, die in einer Ebene parallel zu der Ebene durch
die Punkte R, G und B liegen. Eine dieser Ebenen ist die Ebene durch C, M und Y. Der Durchschnitt
einer derartigen Ebene mit dem Spat ist ein Polygon mit drei oder sechs Ecken. Jeder dieser Durchschnitte
lässt sich beschreiben durch die Menge
von Ortsvektoren mit einem festen k zwischen 0 und 3 . Für bzw. ist bzw. . Die
Eckpunkte eines gezeichneten Dreiecks sind dadurch ausgezeichnet, dass zwei der Vorzahlen r, g und b
entweder beide 0 oder beide 1 sind. Bei einem Sechseck sind die Eckpunkte dadurch bestimmt, dass
sowohl die 1 als auch die 0 unter den Vorzahlen vorkommt. Wenn r, g und b übereinstimmen, ist der
zugehörige Farbpunkt ein grauer Punkt auf der Geraden durch S und W. Er ist der Schwerpunkt des
gezeichneten Dreiecks oder Sechsecks.