Es lebe die Geometrie!

Catalanische Körper ohne Symmerie-Ebenen

Dies sind die zu den archimedischen Körpern ohne Symmetrie-Ebenen polaren Körper. Sie ergeben
sich also aus dem Cubus simus oder dem Dodecaedron simum als Durchschnitt der Halbräume, die
zu den Tangential-Ebenen an die Umkugel in den Eckpunkten gehören.

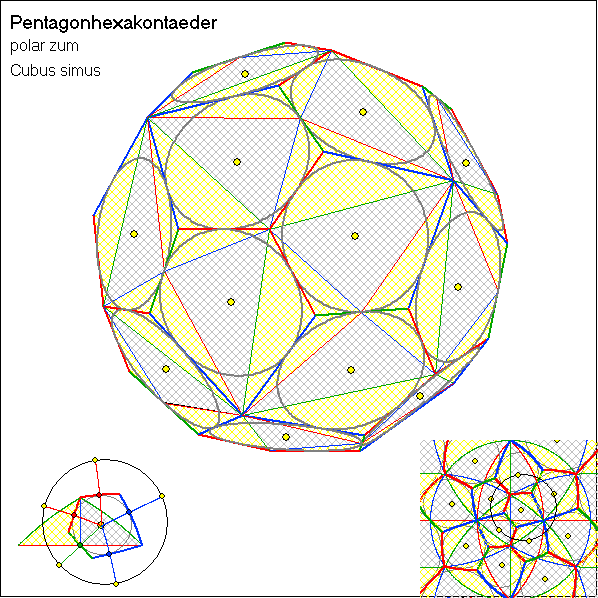
Die Bilder 1 und 2 der Gleitschau zeigen die catalanischen Körper, die zu den beiden Modifikationen
des Cubus simus gehören. Sie sind spiegelbildlich zueinander. In Bild 1 entsprechen die grauen Dreiecke
in den fünfeckigen Seitenflächen des Pentagonhexakontaeders den grauen Kacheln der Würfel-Kachelung.
Die gelben Kacheln der Würfel-Kachelung sind dagegen in drei Teil-Dreiecke zerlegt, die jeweils
verschiedenen Seitenflächen des catalanischen Körpers zugeordnet sind. In Bild 2 sind die Rollen der
gelben und grauen Dreiecke vertauscht. Die Bilder 3 und 4 zeigen, dass die Teilungspunkte jeweils über
der Mitte eines Dreiecks des Cubus simus liegen. Bild 5 entsteht aus Bild 1 durch Zufügung der Bögen, die
zu den Seiten der Würfel-Kachelung auf der Kugel gehören. Bild 6 zeigt dazu die Verbindungsgeraden
der K-Eckpunkte dieser Kachelung mit dem Kugel-Mittelpunkt O. Sie treffen C-Eckpunkte oder die
Mitten der grünen Kanten des catalanischen Körpers CK. Bild 7 stellt das Poincare-Modell der Würfel-
Kachelung dar, zusammen mit den stereographischen Bildern der Großkreis-Bögen, die in den Ebenen
durch die Kanten des catalanischen Körpers und O liegen. In Bild 8 sind die entsprechenden Bögen
für die Kanten des zugehörigen archimedischen Körpers mit dünnem Strich hinzugezeichnet. Bild 9
zeigt das entsprechende Klein-Modell, Bild 10 eine Seitenfläche von CK mit den gerundeten Größen
der Innenwinkel.