Es lebe die Geometrie!

Inkegelschnitte räumlicher Dreiecke, deren Eckpunkte
nullpolar zu drei Zylinder-Ellipsen sind

Die Kegelschnitte, um die es auf dieser Seite geht, entsprechen den Inkreisen von Dreiecken der
euklidischen Geometrie. A, B und C seien drei Punkte des Raumes, die drei Zylinder-Ellipsen so
zugeordnet sind, wie es auf der Seite ' Nullpolarität' beschrieben wurde. Zur Beschreibung der
geometrischen Besonderheiten dieser Kegelschnitte ist es sinnvoll, Dreiecke mit dem gleichen
Vorzeichen bei den Distanzmaßen der drei Seiten gesondert zu betrachten, da sich für sie die aus der
euklidischen Geometrie bekannten Beziehungen weitgehend übertragen lassen. Wir nennen diese
Dreiecke 'homogen'. Der Inkegelschnitt K (kurz: Inkonik) eines homogenen Dreiecks ABC hat die
Eigenschaft, dass die Gerade jeder Dreieckseite berührt wird und alle Punkte auf K den gleichen
Distanzmaß-Wert von einem Zentrum haben, das dem Inkreis-Mittelpunkt in der euklidischen
Geometrie entspricht. Wir nennen es 'Inzentrum'. Die Berührpunkte von K sind die Lotfußpunkte vom
Inzentrum auf die Geraden der Seiten (im Sinne auf der vorigen Seite beschriebenen Orthogonalität).
Für nicht homogene Dreiecke kann man ein Inzentrum in gleicher Weise wie für homogene Dreiecke
definieren. Die Distanzmaß-Werte der Lotfußpunkte vom Inzentrum haben dann zwar den gleichen
Betrag, aber ein unterschiedliches Vorzeichen. Darum muss man bei nicht-homogenen Dreiecken unter
der Inkonik das Paar aus einer Hyperbel K und der zugehörigen konjugierten Hyperbel K' verstehen.
Denn die Fußpunkte der Lote liegen zum Teil auf K und zum Teil auf K'. Ein entsprechendes Verfahren
war bei der Umkonik der vorhergehenden Seite nicht nötig, weil dort alle Eckpunkte des Dreiecks auf
der gleichen Konik lagen.

Die Gleitschau mit dem Dreieck ABC in Orthogonal-Projektion soll klären, inwieweit die Maß-Regeln
für den Inkreis eines Dreieck in der euklidischen Geometrie auf die Inkonik übertragbar sind. Dabei
konzentrieren wir aus auf den Inkreisradius r und die Entfernungen der Dreieckseckpunkte von den
Berührpunkten des Inkreises auf den anliegenden Seitengeraden. Wie nennen diese Werte 'Eckabstände'.
Zur Berechnung dieser Größen werden in der euklidischen Geometrie häufig die Abkürzungen S für den
doppelten Dreiecks-Flächeninhalt und , ,
und benutzt, wobei a, b und c die Längen der Seiten BC, CA und AB bezeichnen.
Dann gilt und die Eckabstände sind , und .
( Siehe dazu 'Schwerpunktskoordinaten in der Dreiecksgeometrie'
--> https://www.vivat-geo.de/Pdf-Dateien/Schwerpunktskoordinaten.pdf)

Diese Größen spielen bei homogenen Dreiecken auch in unserer Geometrie eine Rolle.

In der euklidischen Geometrie wird der Inkreis-Mittelpunkt durch das Schwerpunktskoordinaten-Tripel
(a,b;c) bestimmt. Unser Distanzmaß entspricht dem
Quadrat der Seiten-Länge von AB. Dabei sind und die Koordinaten-
Quadrupel von A und B. Da d(A;B) auch negativ sein kann, ergibt das Wurzelziehen nicht immer eine
reelle Zahl. Als Entsprechung der Seitenlänge von AB in unserer Geometrie betrachten wir darum die
Wurzel des Betrags von d(A;B). Das Zentrumunserer Inkonik hat dann das Schwerpunktskoordinaten-
Tripel , also das Quadupel
.
Wenn man dieses Quadrupel durch ein gleichwertiges Quadrupel ersetzen will, das also
als vierte Komponente eine 1 hat, muss man es durch teilen. Die
Gleitschau zeigt dann, dass bei homogenen Dreiecken jeder Eckpunkt E zu den beiden Berührpunkten
der Inkonik, die auf den Seitengeraden durch E liegen, den gleichen Distanzmaß-Wert hat. Diese Zahlen
sind in der Zeichnung in gleicher Farbe wie der Eckpunkt angegeben. Sie stimmen mit den Quadraten von
, bzw. überein, wenn man unter a, b und c die Komponenten des Schwerpunktskoordinaten-
Tripels von versteht.

Für nicht homogene Dreiecke gilt dies im Allgemeinen nicht. Den Distanzmaß-Wert des Punktes A zu
dem Berührpunkt auf der Geraden AB berechnet man mit dem Quadrupel von durch
.,
denn diese Formel gilt für alle Dreiecke.

Die letzten 22 Bilder der Gleitschau zeigen nach den Standbildern der Animation, dass in homogenen
Dreiecken die Geraden, die einen Eckpunkt mit dem Berührpunkt der Inkonik auf der gegenüber
liegenden Seitengeraden verbinden, einen gemeinsamen Punkt haben. Dieser 'Gergonne-Punkt' hat
hier wie in der euklidischen Geometrie das Schwerpunktskoordinaten-Tripels 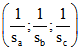. Für nicht
homogene Dreiecke gibt es diesen gemeinsamen Punkt nur in Ausnahmefällen.

Die Gleitschau zeigt zum Dreieck ABC neben der Inkonik mit dem grauen Zentrum auch die
Kegelschnitte, die den Ankreisen der euklidischen Geometrie entsprechen. Wir nennen sie A-Ex-Konik,
B-Ex-Konik und C-Ex-Konik mit den Zentren , und . Wenn wir unter (a;b;c) das Tripel
verstehen, hat das Schwerpunktskoordinaten-Tripel (-a;b;c),
entsprechend (a;-b;c) bzw. (a; b;-c) für und . Die Berührpunkte der Ex-Koniken ergeben sich
wie bei der Inkonik als Lotfußpunkte auf die Seitengeraden von ABC. Die Distanz-Maße ,
und des Eckpunkts A zu dem Lotfußpunkt von , bzw. auf die Gerade AB werden
nach der oben angegebenen Formel für durch Ersetzung von bestimmt. Für homogene
Dreiecke kann man stattdessen die Werte nehmen, die man wie in der euklidischen Geometrie mit
Hilfe von , , und berechnet. In der Zeichnung werden die Eck-Distanzen in den Zeilen mit
dem Zeichen D? angezeigt, wobei man für ? nacheinander o, a, b und c einsetzen muss.
Das Dreieck hat stets das Ortho-Zentum und ABC als Lotfußpunkt-Dreieck.

Zum Teil wird neben den Inkonik-Paar nur das B-Ex-Konik-Paar angezeigt, um die Zeichnung nicht
zu überladen.

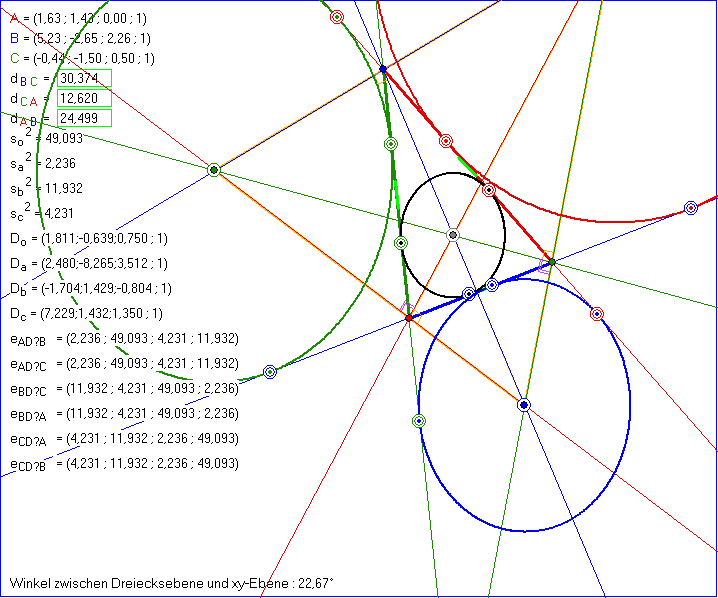
Die Gleitschau soll zeigen, wie sich die Sätze zum Gergonne-Punkt und zum Nagel-Punkt
eines Dreiecks in der euklidischen Geometrie auf ein homogenes Dreieck ABC unsere Laguerre-
Geometrie übertragen lassen. Während der Schnittpunkt der Geraden ist, die einen Eckpunkt
von ABC mit dem Berührpunkt der Inkonik auf der gegenüberliegenden Seiten-Geraden verbindet,
muss man bei statt des Inkonik-Berührpunktes den Berührpunkt der gegenüberliegenden
Ex-Konik nehmen. kann wie in der euklidischen Geometrie mit dem Schwerpunktkoordinaten-
Tripel 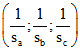berechnet werden und mit dem Tripel .

Die Ex-Nagelpunkte , und mit den Schwerpunktkoordinaten-Tripeln ,
und bilden ein Dreieck mit dem Ortho-Zentrum , das aus dem Dreieck
der Ex-Konik-Zentren durch Streckung entsteht. Diese Streckung hat den Faktor -2 und
als Zentrum das schwarz gezeichnete Bary-Zentrum von ABC. Ein zum Tripel
von äquivalentes Tripel erhält man, wenn man
im Tripel von a durch -a ersetzt. ist der
Schnittpunkt der Verbindungsgeraden von A bzw. B bzw. C mit Berührpunkten auf gegenüberliegenden
Seitengeraden von der Inkonik bzw. der C-Ex-Konik bzw. der B-Ex-Konik.

Wenn man bei den Schwerpunktkoordinaten-Tripeln der Ex-Nagel-Punkte jede Komponente durch
ihren Kehrwert ersetzt, erhält man das braun markierte Dreieck der Ex-Gergonne-Punkte .
ist der gemeinsame Punkt der Geraden, die einen Eckpunkt mit dem Berührpunkt der A-Ex-Konik
auf der gegenüberliegenden Seitengerade verbindet.