Es lebe die Geometrie!

Die Pseudosphäre

--> https://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf

Eugenio Beltrami (1835-1900) erkannte im Jahr 1868 die Bedeutung der von Joseph Liouville
(1809-1882) 'Pseudosphäre' genannten Fläche für eine Interpretation der nicht-euklidischen Geometrie.
Er zeigte, dass geodätische Linien (Geodäten) auf der Pseudosphäre ähnliche Eigenschaften haben,
wie Geraden in der euklidischen Geometrie. Eine Geodäte g hat die Eigenschaft, dass sie zwischen
zwei beliebigen Punkten P und Q auf g, die nicht zu weit auseinander liegen, die kürzeste Verbindung
herstellt. Ein Gummiband, das zwischen P und Q so gespannt wird, dass es auf der Pseudosphäre aufliegt,
passt sich also dem Verlauf von g an.

Verbindet man drei Punkte der Pseudosphäre durch Geodäten, so dass ein Dreiseit entsteht,
dann lassen sich dafür Mittelsenkrechten, Höhen, Seitenhalbierende und Winkelhalbierende mit
Hilfe der Weglängen auf der Pseudosphäre und der euklidischen Winkel zwischen Geodäten
definieren. Es zeigt sich, dass dafür ähnliche Schnittpunkts-Sätze gelten wie in der euklidischen
Geometrie. Aber anders als in der euklidischen Geometrie hat nicht jedes Rechteck mit drei rechten
Winkeln auch an der vierten Ecke einen rechten Winkel.

Die Pseudosphäre entsteht dadurch, dass die Traktrix (oder Schleppkurve) genannte Kurve um
ihre Asymptote rotiert. In der Animation ist die Traktrix als gelb-graue Linie in der x-z-Ebene
eines dreidimensionalen Koordinatensystems eingezeichnet, zusammen mit sieben Linien, die daraus
durch Rotation um die z-Achse entstehen. Wenn man von einem beliebigen Punkt A der z-Achse die
Tangenten an diese Linien legt, dann haben deren Berührpunkte von A stets den gleichen Abstand 1.
Die rot gezeichneten Strecken haben im Raum also für alle Punkte A der z-Achse die gleiche Länge.

Die Traktrix in der x-z-Ebene kann mit Hilfe einer Funktion z = f(x) beschrieben werden. In einem
Steigungsdreieck, das die rote Strecke als Hypotenuse hat, ist x die Länge der horizontale Kathete
und die der vertikalen Kathete. Darum ist und folglich ,
da f monoton fallend ist. Demnach ist 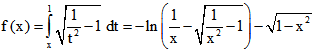für .
Zur Beschreibung der Pseudosphäre nützen Polarkoordinaten r und w in der x-y-Ebene, wobei r den
Abstand eines Punktes P(x ; y ; 0) vom Punkt N(0 ; 0 ; 0) angibt und w den Winkel ENP für E(1 ; 0 ; 0).
In einer Beschreibung mit Zylinderkoordinaten ist dann die Pseudosphäre durch die Gleichung z = f(r) gegeben.

Die Traktrix heißt auch Schleppkurve aus folgendem Grund: Wenn man einen schweren Gegenstand
(ohne Räder) an einem Band längs einer Geraden h zieht, dann bewegt sich der Schwerpunkt des
Gegenstandes auf einer Traktrix, die h als Asymptote hat, falls die Unterlage des Gegenstandes keine
Unregelmäßigkeiten enthält.

Schon vor Beltrami war erkannt worden, dass die Pseudosphäre eine Fläche mit konstanter negativer
Gauss-Krümmung -1 ist. Dies bedeutet Folgendes: P sei irgendein Punkt der Pseudosphäre und g eine
Gerade durch P, die senkrecht auf der Pseudosphäre steht. Eine Ebene, die g enthält, schneidet dann
aus der Pseudosphäre eine Kurve heraus. Es gibt zwei dieser Ebenen, für welche die Krümmung
der Schnittkurve in P extremal ist, nämlich die Ebene T, die die z-Achse und die Traktrix durch P enthält,
und die dazu senkrecht stehende Ebene S. Die Schnittkurve t von T ist die Traktrix durch P. Wenn r
der Abstand des Punktes P von der z-Achse ist, dann ist der Krümmungsbetrag der Traktrix in P durch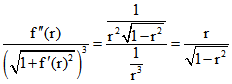
gegeben. Die Schnittkurve s in S hat eine kleinere Krümmung als
der Breitenkreis durch P, dessen Krümmung ist, da dieser Kreis zwar in P die gleiche Tangente wie s hat,
aber nicht in S liegt. Nach dem unten erklärten Satz von Meusnier ist dann die Krümmung von s gleich ,
wobei a der Winkel zwischen S und der Ebene des Breitenkreises ist. a stimmt mit der Größe des Winkels
zwischen der oben genannten roten Strecke auf der Traktrix-Tangente in P und der z-Achse überein. Darum ist
und die Krümmung von s folglich . Da die Schnitt-Kurven
s und t auf unterschiedlichen Seiten der Tangentialebene in P liegen, gibt man ihren Krümmungen ein
unterschiedliches Vorzeichen, so dass das Produkt der Krümmungen negativ ist. Dieses Produkt wird als
Gauss-Krümmung definiert. Es beträgt also .

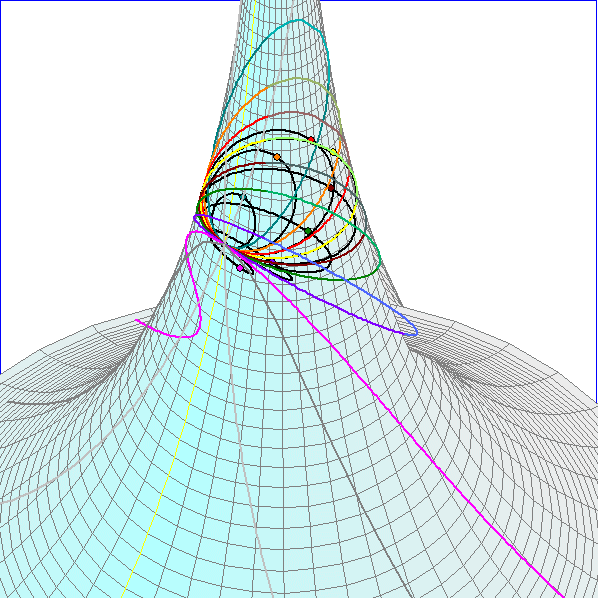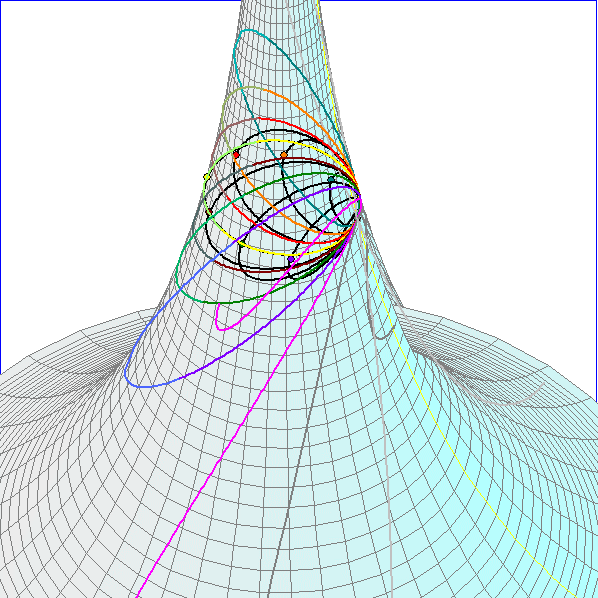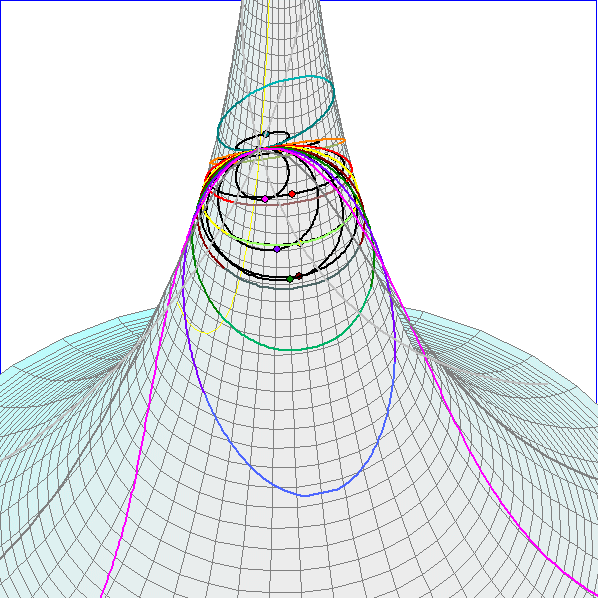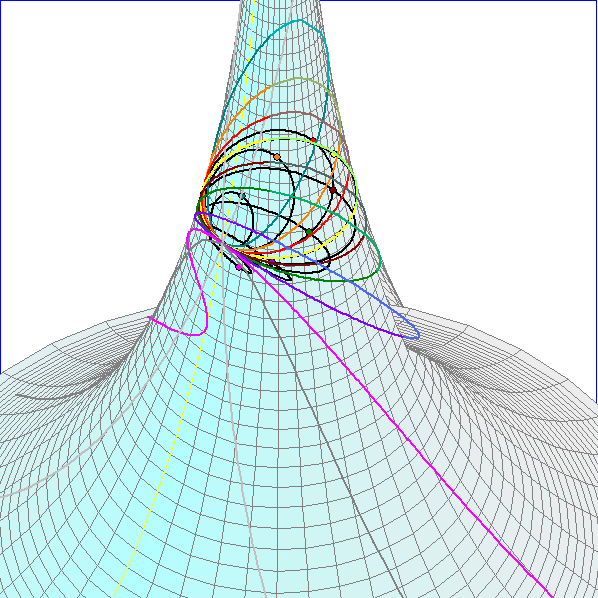
Die farbig gezeichneten Kurven auf der Pseudosphäre sind Schnittkurven mit Ebenen durch den Punkt
P(0,2 ; 0 ; f(0,2)), die auch die Tangente in P an den durch P laufenden Breitenkreis enthalten, so dass
der Winkel zwischen benachbarten Ebenen 18° beträgt. Die schwarzen Kurven sind die Kreise, die sich
diesen Schnittkurven im Punkt P optimal anschmiegen. Der Radius eines schwarzen Kreises ist folglich der
Krümmungsradius des zugehörigen farbigen Kreises im Punkt P, der Kehrwert davon also die Krümmung
in P. Diese Schmiegkreise liegen nach dem Satz von Meusnier (sprich 'Möniee') auf einer Kugel.
Wenn man Schnittebenen betrachtet, die eine andere Tangente in P enthalten, dann ergibt sich eine
andere Kugel.