Es lebe die Geometrie!

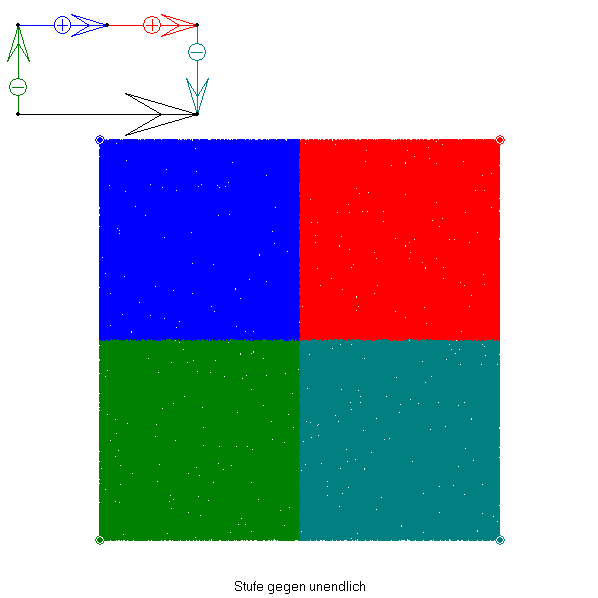
In jeder Stufe ergibt sich hier ein zusammenhängender Streckenzug. Manche Strecken werden dabei
hin und gleich danach zurück gezeichnet. Die Folge dieser Streckenzüge konvergiert gegen eine Kurve,
die ein Quadrat vollständig ausfüllt.

Die Animation zeigt den Aufbau des Streckenzugs in der Stufe 4 und die anschließende Gleitschau den
Aufbau in den Stufen 2 und 3. Man erhält diesen Ablauf, wenn man in dem Visual Basic-Programm
der Seite Blatt die Prozedur Fraktal durch folgenden Code ersetzt:

Private Sub Fraktal(Stufe As Integer, Pixelweite As Double, inv As Integer)
If Stufe = 0 Then
If inv = 1 Then
tmove(pixelweite, True, Color.Blue)
Else
tmove(pixelweite, True, Color.Red)
End If
Else
turn(90 * inv)
Fraktal(Stufe - 1, 0.5 * Pixelweite, -inv)
turn(-90 * inv)
Fraktal(Stufe - 1, 0.5 * Pixelweite, inv)
Fraktal(Stufe - 1, 0.5 * Pixelweite, inv)
turn(-90 * inv)
Fraktal(Stufe - 1, 0.5 * Pixelweite, -inv)
turn(90 * inv)
End If
End Sub