Es lebe die Geometrie!

Verwandte des Reuleaux-Dreiecks

-->Figuren mit konstanter Breite
https://www.vivat-geo.de/Pdf-Dateien/Gleichdick.pdf

Unter einem Verwandten des Reuleaux-Dreiecks verstehen wir ein Kreisbogen-Polygon, das ein
Gleichdick ist, bei dem also alle umschließenden Tangenten-Rechtecke Quadrate mit gleicher
Seitenlänge sind und das eine konvexe Menge berandet.

Die Animation zeigt, dass das Kreisbogen-Polygon über dem Pentagramm ein Gleichdick ist.
Es wird hier als 1-Kurve zur Drehpunktfunktion erzeugt.
Die in der Gleitschau auf die Animation folgenden Bilder sind Standbilder daraus oder entsprechende
Bilder mit den Eckenzahlen 7, 2, 4 und 6. Bei der Eckenzahl 7 ergibt sich ebenfalls ein Gleichdick,
nicht aber bei den geraden Eckenzahlen 2, 4 und 6. Allgemein gilt:

Die 1-Kurve zur Drehpunktfunktion mit einer natürlichen
Zahl n >1 ist genau dann ein Gleichdick, wenn n ungerade ist. Dies folgt aus dem Satz auf der Seite
Begründung , da hier die Bedingung für alle nur bei ungeradem n gilt.

Hier wird deutlich, dass die Gleichdick-Eigenschaft nicht voraussetzt, dass das Kreisbogen-Polygon
regelmäßig ist. Bei dem in der Animation gezeigten Fünfeck waren die Sprungstellen 10°, 20° und 70°
der Drehpunktfunktion weitgegend frei gewählt worden. Die nächsten beiden Sprungstellen 120,53°
und 165,64° waren dann dadurch festgelegt, dass die Spitze R (rot) des Pfeils nach einer Drehung um
180° mit seinem ursprünglichen Anfangspunkt G (gelb) zusammenfallen muss, damit eine geschlossene
Randkurve eines Gleichdicks entsteht. Siehe dazu die Seite Begründung. Der gedrehte Pfeil liegt dann also
mit entgegengesetzter Orientierung auf dem ursprünglichen Pfeil. Dies wird in der Gleitschau im Anschluss
an die Animation an Hand der 18 Standbilder zu den Richtungswinkeln 0°, 20°, 40°,..., 360° deutlich.
Daran schließt sich das Bild eines Gleichdick-Fünfecks mit den Sprungwinkeln 20°, 40°, 60°, 103,2° und
156,08° an. Das folgende Bild gehört zu den ersten drei Sprungwinkeln 10°, 20° und 80°. Daraus berechnet
man nach dem unten angegebenen Verfahren als vierte und fünfte Sprungwinkel-Größen 140° und 190°.
Da 190° aber größer als 180° ist, schließt sich die rote 1-Kurve nicht, so dass kein Gleichdick entsteht.
Denn für die Sprung-Winkel in dem grau gezeichneten Teil des Graphen der Drehpunktfunktion muss im
Fall des Gleichdicks gelten:

ist genau dann Sprungwinkel zwischen 180° und 360°,
wenn Sprungwinkel zwischen 0° und 180° ist.

Dies ist eine Folge der Bedingung ' für alle ', die für jedes Gleichdick gilt, das
zu einer Drehpunktfunktion mit dem Mittelwert Null gehört (siehe Begründung).

Zur Berechnung des vierten und fünften Sprungwinkels beim Kreisbogen-Fünfeck:
Die zugehörige Drehpunktfunktion f ist eine Treppenfunktion, die bei den Sprungwinkeln für k gleich
1 bis 5 zwischen den Werte -1 und 1 hin- und herspringt. Damit ein Gleichdick entsteht muss gelten: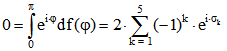
. Darum ist die gegebene Summe gleich
der Summe . In der komplexen Ebene bilden also die Punkte 0, und ein
gleichschenkliges Dreieck mit den Richtungswinkel und , den Schenkellängen 1 und dem
Betrag r von S als Basislänge. sei der Richtungswinkel von S. Die beiden gesuchten Winkelgrößen
sind dann und .

Die roten Kurven sind Evolventen des blauen Fourier-Polygons PS(8,3,1) zur Drehpunktfunktion
, die durch die Fourier-Reihe und durch
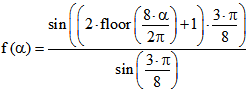dargestellt wird. Der Graph von f ist eine Treppenkurve mit acht
gleich breiten Stufen, deren Mitten auf dem Graphen von 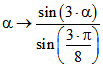liegen. f hat folglich den Mittelwert
Null, 1 als obere Schranke und es gilt für alle . Darum ist die 1-Kurve ein Gleichdick.
Die in der Animation gezeigten s-Kurven mit s zwischen 0 und 1 haben mit dem Gleichdick die Eigenschaft,
dass alle Tangenten-Rechtecke Quadrate mit der Seitenlänge 2s sind.

Die Drehpunktkurve dieser Animation gehört zur Drehpunktfunktion mit
den Darstellungen 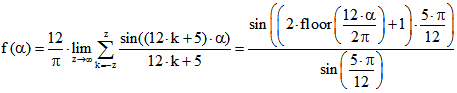. Der
Graph von f ist eine Treppenkurve mit 12 gleich breiten Stufen, deren Mitten auf dem Graphen von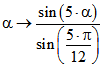
liegen. Auch hier ist die 1-Kurve ein Gleichdick.
In entsprechender Weise kann zu allen Fourier-Polygonen FS(n,m,1) und FC(n,m,1) mit geradem n und
ungeradem m ein Gleichdick konstruiert werden, da dann die Vorzahlen von im Term
bzw. alle ungerade sind und folglich für alle gilt.