Es lebe die Geometrie!

Die Kurve der Spektralfarben

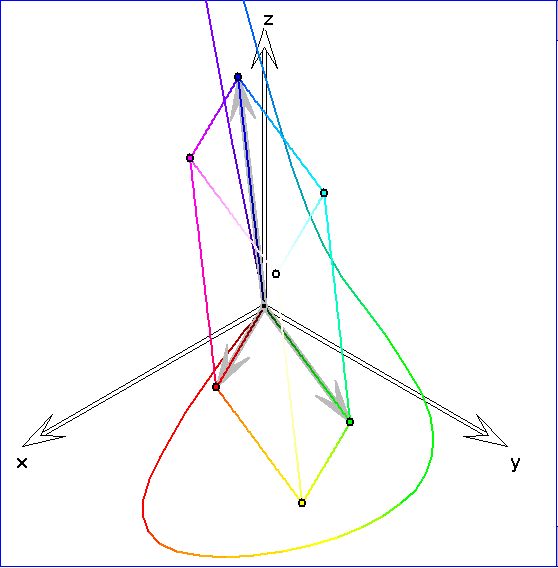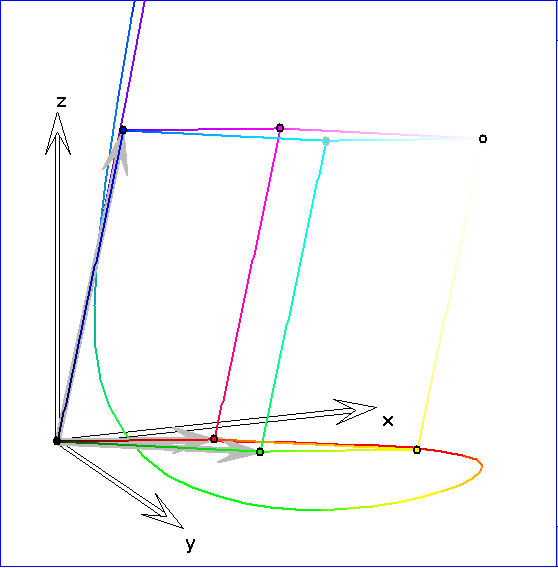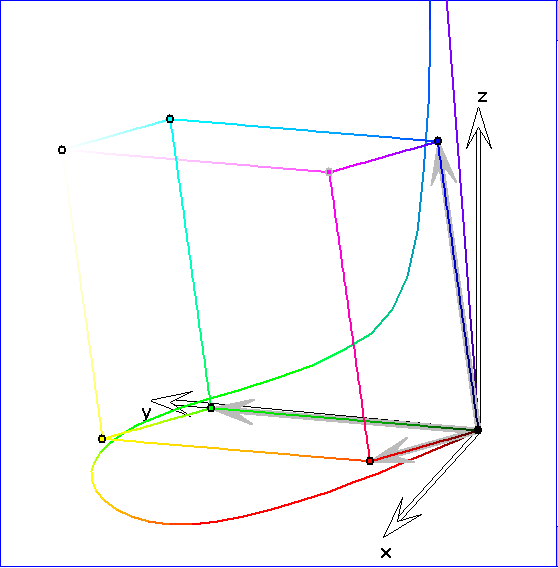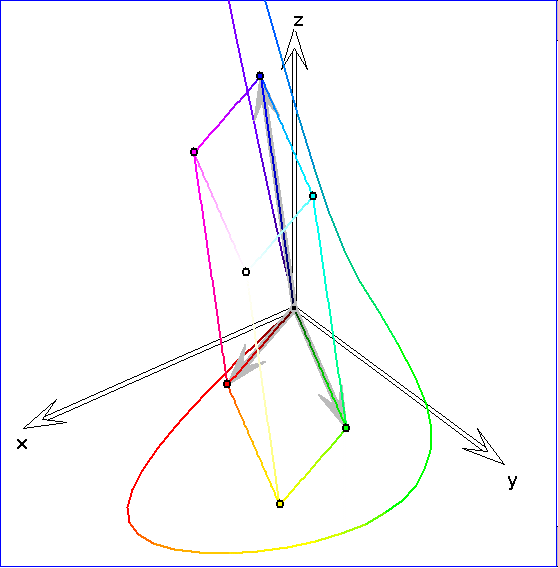
Zum sRGB-Parallelepiped ist hier die Kurve hinzugezeichnet, deren Punkte zu reinen Spektralfarben
gehören, die nicht durch ein Gemisch von Licht verschiedener Wellenlängen zustandekommen, sondern die
durch genau eine Wellenlänge l im Bereich des sichtbaren Lichts zwischen l = 380nm und l = 780nm
bestimmt sind. Dabei wird vorausgesetzt, dass die Energie des Lichts für alle Wellenlängen gleich groß ist.
Ein Kurvenpunkt beschreibt den Farbeindruck eines normalen menschlichen Beobachters beim Betrachten
einer mit Licht der Wellenlänge l beleuchteten Fläche. Dabei wird ein x-y-z-Koordinatensystem
zugrundegelegt, das auf einer von der Internationalen Beleuchtungskommission CIE festgelegten Konvention
beruht. ( http://www.cie.co.at/index.php/LEFTMENUE/DOWNLOADS --> 'Selected colorimetric Tables'
--> 'CIE 1931 standard colorimetric observer'). Die hier für die Darstellung der Punkte der Spektralkurve
benutzten Farben geben nur näherungsweise die zugehörigen Spektralfarben wieder, da hier nur die die Farben
benutzt werden, die zu den Punkten im sRGB-Spat gehören. Wenn , und die Ortsvektoren des
Rot-Punktes R, des Grün-Punktes G und des Blau-Punktes B des sRGB-Spats sind und der Ortsvektor
eines Punktes P der Spektralkurve als Linearkombination dargestellt wird, dann ist
die hier für P benutzte Farbe die Farbe des Punktes im sRGB-Spat, den man erhält, wenn man die Vorzahlen
r, g, und b, die größer als 1 bzw. kleiner als 0 sind, durch 1 bzw. 0 ersetzt.

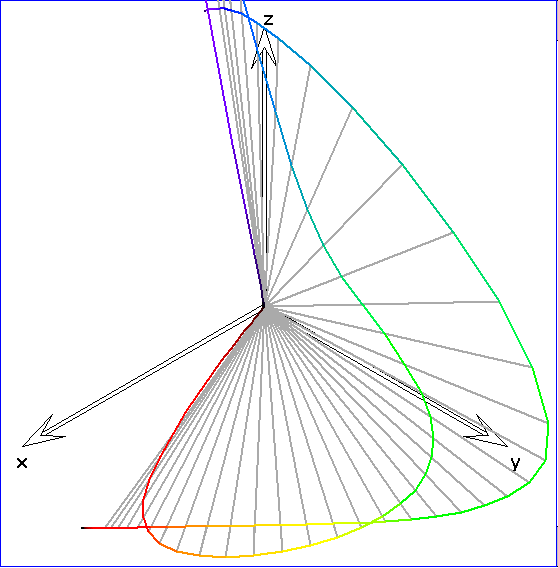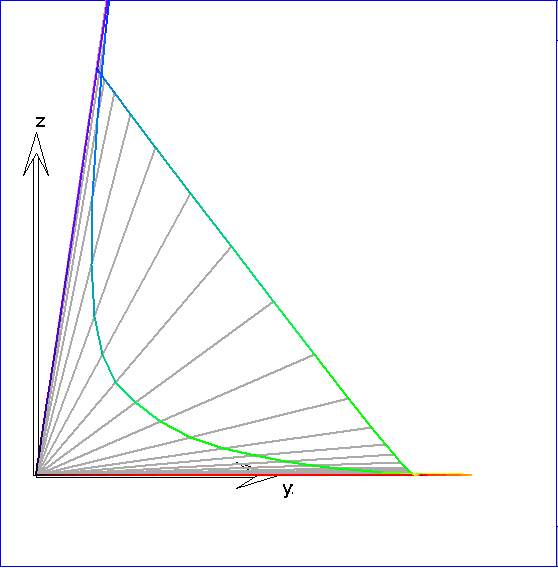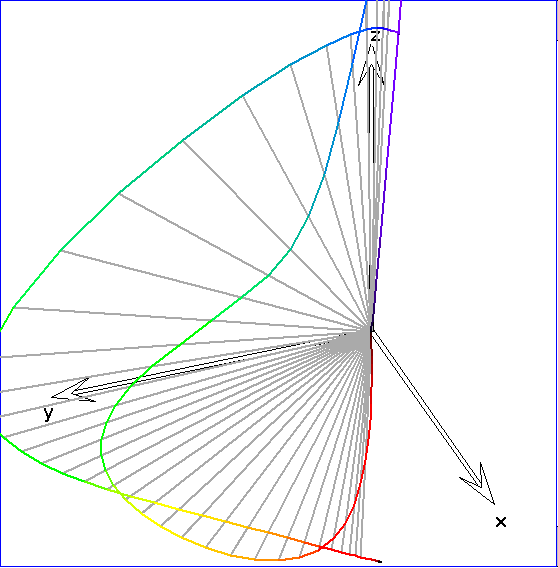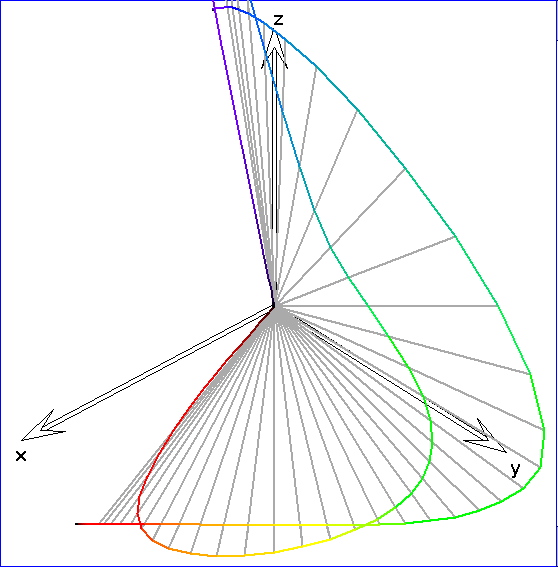
In dieser Abbildung werden die Urprungsgeraden durch die Spektralkurvenpunkte mit einer Ebene E
geschnitten und die Kurve der Schnittpunkte dargestellt. E ist die Ebene durch den Graupunkt Gr
in der Mitte zwischen dem Schwarz-Punkt S und dem Weiß-Punkt W des sRGB-Spats, die senkrecht
auf dem Ortsvektor von Gr steht. Die Farben zu Punkten einer Ursprungsgeraden unterscheiden sich lediglich
in ihrer Helligkeit. Insofern ist jeder Ursprungsgeraden durch einen Punkt, der eine Farbvalenz beschreibt,
die zugehörige 'Farbart' zugeordnet. Die Kurve ist bemerkenswerter Weise konvex. Das bedeutet, dass sie
Teilmenge der Randkurve ihrer konvexen Hülle ist. Dabei ist die konvexe Hülle von definiert als die
kleinste umfassende Punktmenge, die mit je zwei ihrer Punkte P und Q auch die Verbindungsstrecke
enthält.

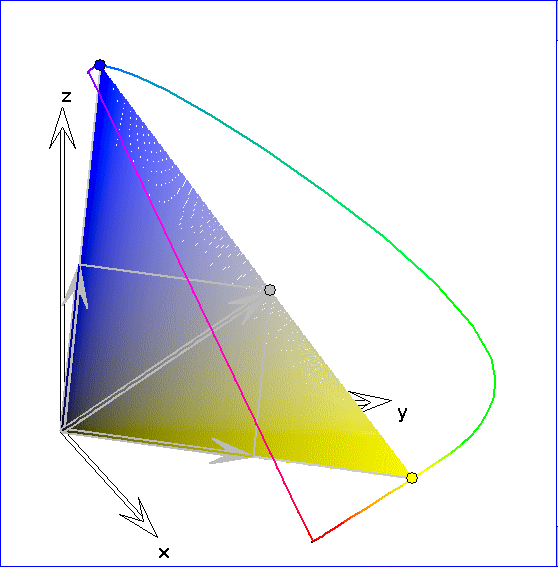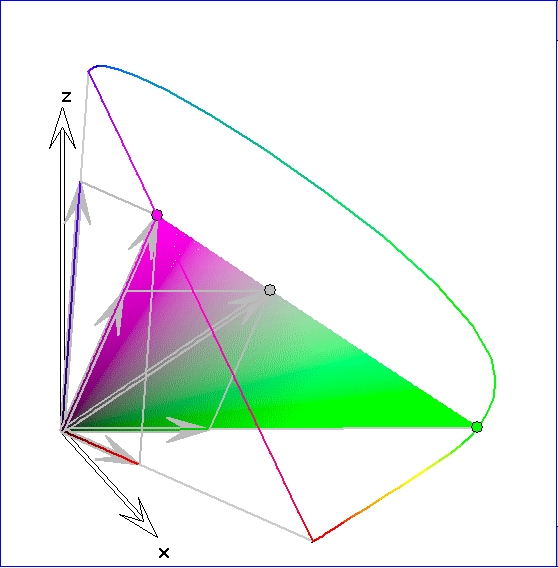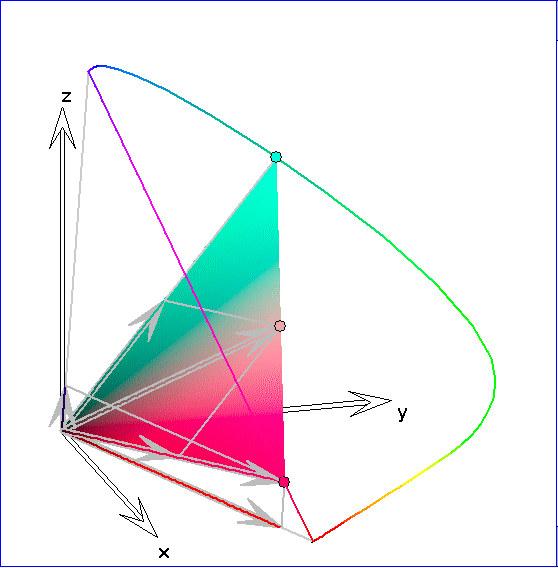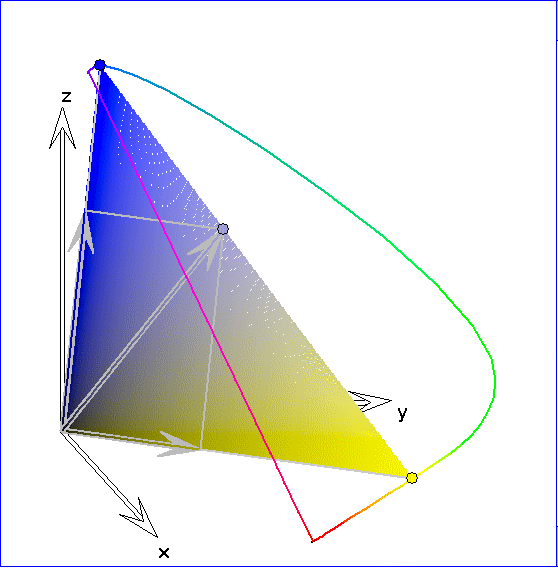
Die Kurve ist hier durch eine Strecke zwischen einem roten Punkt und einem blau-violetten Punkt
in der Nähe der Endpunkte von ergänzt. Durch das farbig gezeichnete Dreieck soll dargestellt werden,
dass sich die Farbvalenz zu irgeneinem Punkt P im Innern der konvexen Hülle von auf verschiedene Weisen
durch additive Farbmischung aus zwei oder drei Spektralfarben ergibt. P durchläuft in dieser Darstellung zyklisch
die Punkte Gr, , und , wobei die Punkte die Mittelpunkte zwischen dem Graupunkt Gr und den
Schnittpunkten der Ursprungsgeraden SR, SG und SB mit der Ebene E sind. Dass sich die zugehörigen Farben
auf unterschiedliche Weisen mischen lassen, drückt sich geometrisch darin aus, dass sich der Ortsvektor von P
auf unterschiedliche Weisen als Linearkombination von Ortsvektoren zu zwei oder drei Spektralfarbenvektoren
ergibt. Wenn P der Graupunkt Gr ist und zwei Spektralfarbenvektoren ausreichen, dann gehören die beiden
Spektralfarben zu komplementären Farbarten.