Es lebe die Geometrie!

Erzeugung einer Penrose-Kachelung
mit Drehstreckungen und Streckspiegelungen

Die Animation zeigt, wie das matt gezeichnete sehr kleines Anfangsstück einer Penrose-Kachelung
mit nur zwei Boot-Kacheln sich aus einem noch kleineren Pfeilzug in Form einer Zwille mit Hilfe von
Drehstreckungen und Streckspiegelungen ergibt. Die fünf Pfeile der Zwille sind in der Zeichnung oben
links mit einem Vorzeichen versehen. Zu einem Plus-Pfeil bzw. Minus-Pfeil gehört die Drehstreckung
bzw. Streckspiegelung, die den scharzen Start-Pfeil in den Plus-Pfeil bzw. Minus-Pfeil abbildet. Diese
Darstellungsform zur Festlegung von Ähnlichkeits-Abbildungen wird auch bei der Beschreibung von
Fraktalen benutzt (siehe dazu die Seite ' Spiralen 1' und auch die darauf folgenden). Bei der Untersuchung
von Fraktalen wird der schwarze Start-Pfeil auch als 'Initiator' bezeichnet und die Menge der farbigen
Pfeile als 'Generator'.

Die Länge der Generator-Pfeile ergibt sich aus der des Start-Pfeils durch Multiplikation mit der kleinen
goldenen Zahl . Die Richtugswinkel der Generator-Pfeile unterscheiden sich vom
Richtungswinkel des Start-Pfeils um ein ganzzahliges Vielfaches von 36°. Der Vergleich mit den
vorangegangenen Seiten über Penrose-Kachelungen zeigt, dass der Start-Pfeil zu den Generator-Pfeilen
die gleiche Lage hat, wie Rand-Pfeile von Boot- oder Kronen-Kacheln zu einem Flächen-Pfeil.

In dem beweglichen Teil der Animation wird eine Zwille mit scharzen Spitzen aus einer Anfangsstellung
wie im Generator oben links in einen Teil der matt gezeichneten Kachelung aus zwei Boot-Kacheln
übergeführt. Die Endposition ist dabei die, welche sich bei Anwendung der oben definierten Ähnlichkeits-
Abbildungen ergibt. Die umrandeten Punkte sind die Fixpunkte dieser Abbildungen. Im Fall der Dreh=
streckungen sind auch alle Zwischen-Bilder ähnlich zu der Ausgangs-Zwille. Bei den Streckspiegelungen ist
dies nicht möglich, weil die Zwille um das mitbewegte Bild des Start-Pfeils geklappt werden muss. Nach
diesem Prozess mit allen fünf Generator-Pfeilen sind alle matt gezeichneten Kachelungs-Pfeile überdeckt,
an einigen Stellen sogar mehrfach. Die Pfeile der Kachelung sind die Bilder des Start-Pfeils bei
Hintereinanderschaltungen von zwei der den Generator-Pfeilen zugeordneten Ähnlichkeits-Abbildungen,
wobei dies auch zwei gleiche Abbildungen sein können.

Wir ordnen dem Start-Pfeil die Zahl n = 0 zu, der Zwille n = 1 und der Menge der Bilder von
Hintereinanderschaltungen zweier Ähnlichkeits-Abbildungen n = 2.

In dieser Animation wird der Übergang von einer Pfeilmenge der Ordnugszahl 2 zu der mit der
Ordnungszahl 3 dargestellt. Man erkennt eine nicht ganz vollständige Kronen-Kachel der Stufe 2.
Die Pfeile zur Ordnungszahl 3 sind die Bilder des Start-Pfeils bei Hintereinanderschaltungen von
drei der den Generator-Pfeilen zugeordneten Ähnlichkeits-Abbildungen, wobei diese Abbildungen
teilweise gleich sein können.

Dies zeigt den Übergang von einer Pfeilmenge der Ordnugszahl 3 zur Ordnungszahl 4. Die Pfeile
der Kachelung zur Ordnungszahl 4 sind die Bilder des Start-Pfeils bei Hintereinanderschaltungen
von vier der den Generator-Pfeilen zugeordneten Ähnlichkeits-Abbildungen.

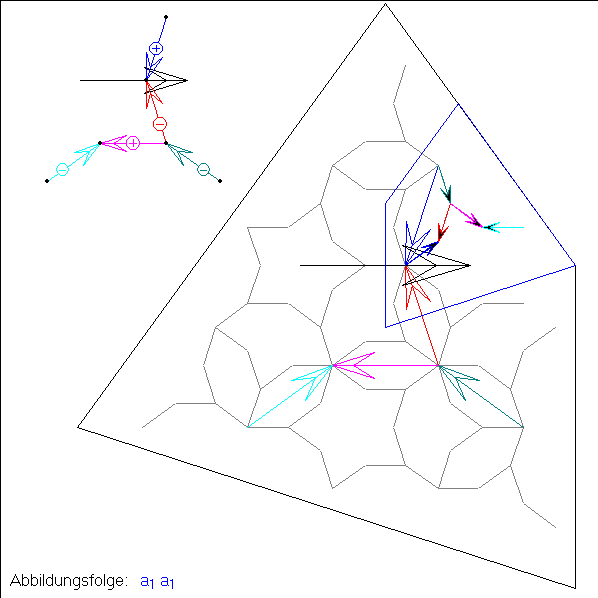
Mit wachsender Ordnungszahl nähert sich die gekachelte Fläche immer mehr einem Drachen-Viereck D mit
drei Innenwinkeln von 72° an. Wenn man die zu den Generator-Pfeilen gehörigen Ähnlichkeits-Abbildungen
bis auf D anwendet, dann liegen die Bilder bis alle in D und füllen D vollständig aus. Außer zu
und gibt es allerdings zu allen Bild-Paaren gemeinsame innere Punkte. Alle fünf Bilder sind kongruent,
da bei allen fünf Ähnlichkeits-Abbildungen der Streckungsfaktor die kleine goldene Zahl ist.
Wenn man in diese Bilder Pfeile in einer Lage einfügt, die der Lage der Generator-Pfeile in D entspricht, ergeben
sich Pfeile zur Kachelung der Ordnungszahl n = 2. Wenn man auf diese Bilder erneut bis anwendet, erhält
man Pfeile zu n = 3.

Bemerkenswert ist die Wirkung der Vertauschung der Reihenfolge bei der Hintereinanderschaltung zweier
Abbildungen. Um zum Beispiel ein Drachen-Viereck zu erhalten, das in die entsprechende Lage wie
in D hat, muss man auf D erst anwenden und danach . Die Gleitschau zeigt Beispiele dazu und
auch zur Hintereinanderschaltung von drei Abbildungen.

Die letzten fünf Bilder der Gleitschau stellen die Wirkung bei vielfacher Hintereinanderschaltung der
gleichen Abbildung dar. Mit wachsender Anzahl der Abbildungen konvergiert die Folge der Bilder
gegen den Fixpunkt der Abbildung. Für die Streckspiegelung zum hellblauen Generator-Pfeil ist dies
ein Eckpunkt von D. Der diesem Fixpunkt gegenüber liegende Eckpunkt ergibt sich, wenn man den
Start-Pfeil mit der goldenen Zahl G als Faktor verlängert. Der gemeinsame Fixpunkt der Abbildungen
zu den beiden rötlichen Generator-Pfeilen teilt alle Winkelhalbierenden des Drachen-Vierecks im
goldenen Schnitt.

Die Gleitschau zeigt Pfeilmengen bis zu n = 6 und Kombinationen mit Pfeilen kleinerer Ordnungszahl.
Bei der Ordnungszahl-Differenz 1 sind dies Flächen-Pfeilen, bei der Differenz 2 Richtungs-Pfeile von
Boot-Kacheln und bei der Differenz 4 markieren sie Kacheln 2. Stufe.

Bei einer ungeraden Ordnungszahl n sind die Generator-Pfeile Richtungspfeile von Boot-Kacheln
der Stufe und der Start-Pfeil Flächen-Pfeil zu einer Stern-Kachel der Stufe .
Bei einer geraden Ordnungszahl n sind die Generator-Pfeile Flächen-Pfeile von Stern -Kacheln
der Stufe und der Start-Pfeil Richtungspfeil zu einer Boot-Kachel der Stufe

In den letzten sechs Bildern der Gleitschau wird die zur Penrose-Kachelung gehörige Kachelung mit
regulären Fünfecken dargestellt.


Zum Rechnen mit den Abbildungen:

Neben der Berechnungsmöglichkeit, die auf der Seite ' Erklärung zu Fraktalen' dargestellt wird, bietet sich
hier ein Weg über komplexe Zahlen an. Dazu sei definiert .
Dann ist , , ,
und .
Für die goldenen Zahlen und und
die goldenen Quadratwurzeln und gilt für alle ganzzahlige n:
, , , .
, , ,
und .
Wenn der schwarze Start-Pfeil den Koordinatenursprung mit dem Punkt bei Eins auf der Rechtsachse
verbindet, lassen sich die den Generator-Pfeilen zugeordneten Ähnlichkeitsabbildungen so beschreiben:
, , ,
, .
Als Fixpunkte ergeben sich , , , und .
Die Eckpunkte von D sind , , und .
Die Seiten haben die Längen und .

Zur Erzeugung der Penrose-Kachelung mit dem Computer kann man anstatt der Ähnlichkeitsabbildungen
ein Turtle-Objekt als Zeichenwerkzeug benutzen. Diese Objekt hat als Eigenschaft einen Winkel zur
Beschreibung der Nasenrichtung einer Schildkröte und verfügt über die Methoden 'turn' zum Ändern der
Nasenrichtung und 'move' zur geradlinigen Bewegung in Nasenrichtung. Das Konzept wurde in dem
Visual Basic-Programm auf der Seite ' Blatt' benutzt. Man erhält statt des dort gezeichneten Blattes eine
Penrose-Kachelung, wenn man die Prozedur Fraktal durch folgenden Code ersetzt:

Private Sub Fraktal(Stufe As Integer, Pixelweite As Double, inv As Integer)
Dim gol As Double
gol = (Math.Sqrt(5) - 1) / 2
If Stufe = 0 Then
If inv = 1 Then
tmove(Pixelweite, True, Color.Blue)
Else
tmove(Pixelweite, True, Color.Red)
End If
Else
tmove(Pixelweite * gol, False, Color.White) : turn(72 * inv)
tmove(Pixelweite * gol, False, Color.White) : turn(180)
Fraktal(Stufe - 1, Pixelweite * gol, inv) : turn(36 * inv)
tmove(Pixelweite * gol, False, Color.White) : turn(180)
Fraktal(Stufe - 1, Pixelweite * gol, -inv) : turn(180)
tmove(Pixelweite * gol, False, Color.White) : turn(36 * inv)
tmove(Pixelweite * gol, False, Color.White) : turn(180)
Fraktal(Stufe - 1, Pixelweite * gol, -inv) : turn(36 * inv)
Fraktal(Stufe - 1, Pixelweite * gol, inv) : turn(36 * inv)
tmove(Pixelweite * gol, False, Color.White) : turn(180)
Fraktal(Stufe - 1, Pixelweite * gol, -inv) : turn(-36 * inv)
tmove(Pixelweite * gol, False, Color.White) : turn(108 * inv)
tmove(Pixelweite * gol, False, Color.White) : turn(-108 * inv)
tmove(Pixelweite * (1 - gol), False, Color.White)
End If
End Sub