Es lebe die Geometrie!

Kontaktkurven mit dem Graf einer Potenzfunktion

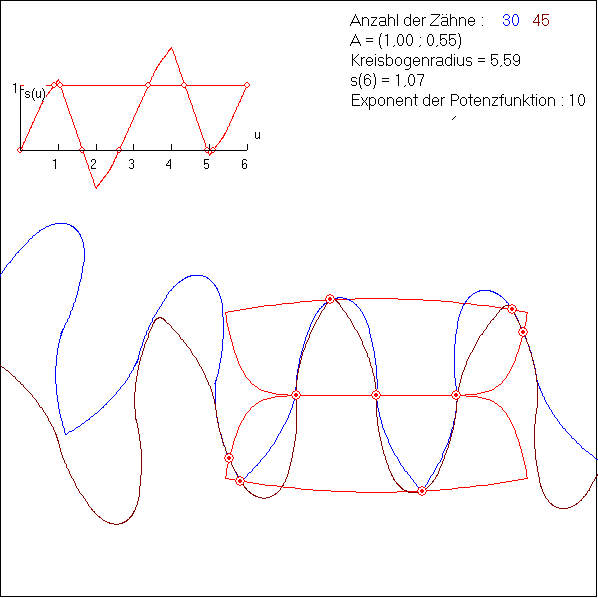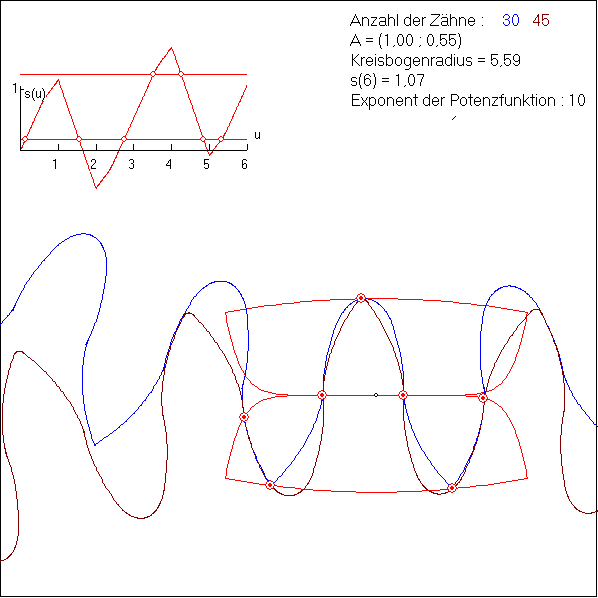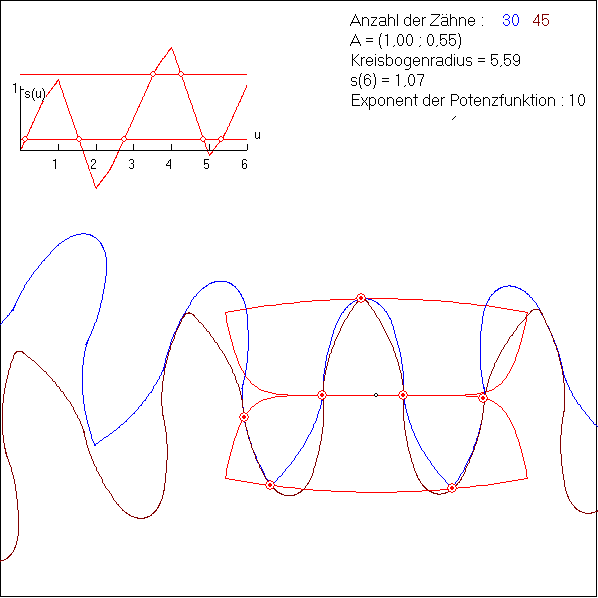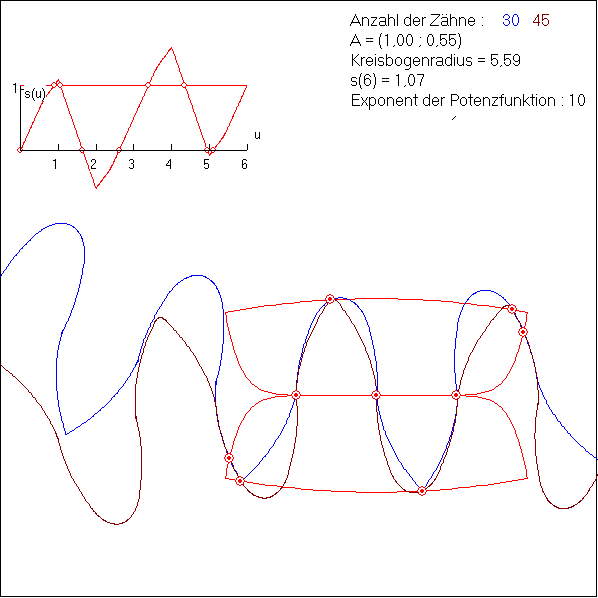
Die Animation zeigt eine Verzahnung, bei der die Kontaktkurve in den Teilstücken 1, 3, 4 und 6 auf dem
Grafen der Potenzfunktion mit a = 0,55 bzw. a = -0,55 liegen. Dies sind die Teilstücke, die
an den Wälzpunkt W = (0 ; 0) im Zentrum der Kontaktkurve grenzen. Die Teile 2 und 5 sind Kreisbögen
mit dem Radius 5,59. Die Besonderheit dieser Verzahnung besteht darin, dass sich der Kontaktpunkt auf
der Zahnflanke zeitweise kaum verschiebt, nämlich dann, wenn er nahezu auf der Rechtsachse y = 0 liegt.
Dabei kommt es zu Selbstüberschneidungen (also Doppelpunkten) der Verzahnungskurve, allerdings auf
einem so kleinen Kurvenstück, dass dieser Effekt in der Zeichnung kaum erkennbar ist.

In dem s(u)-Graf oben links ist dem Teilstück der Kontaktkurve mit der Nummer i das u-Intervall [i-1 ; i]
zugeordnet. Anders als bei der Zykloiden- oder Evolventen-Verzahnung ist der s(u)-Graf in den Teilstücken
Nummer 1, 3, 4 und 6 nicht geradlinig. Aber auch hier sind die Schnittpunkte der eingezeichneten Parallelen
zur u-Achse in gleicher Weise den Kontaktpunkte zugeordnet. Wenn also einer dieser Schnittpunkte die
Koordinate u im Intervall [i-1 ; i] hat, dann teilt der zugehörige Kontaktpunkt die Weglänge seines Teilstücks
im gleichen Verhältnis wie u das Intervall [i-1 ; i] teilt.

Die an die Animation anschließenden Bilder 1 bis 10 zeigen aufeinanderfolgende Positionen der gleichen
Verzahnung. In den Bildern 11 bis 13 wurden die Kreisbögen-Radien variiert. Bild 14 zeigt Verzahnungs=
kurven mit kleinerer Zahnzahl, bei denen es zu deutlichen Selbstüberschneidungen kommt. In den Bildern
15 und 16 wurde der y-Wert des Eckpunktes A oben rechts auf der Kontaktkurve verändert, was zur
Verkleinerung der Kurvenstücke mit Selbstüberschneidungen führte.
In den Bildern 17 bis 26 wurde der Exponent der Potenzfunktion von 10 bis 1 vermindert.
Beim Exponenten 1 ergibt sich eine Evolventen-Verzahnung.

Die Animation stellt die gleiche Verzahnung wie in der Animation darüber mit Geschwindigkeits-
Vektoren dar, die an einem Kontaktpunkt K ansetzen. Die Zahnräder bewegen sich dabei hin und
zurück, so dass K die Kontaktkurve in Form einer '8' durchläuft. Die anschließenden Bilder
1 bis 6 der Gleitschau geben Positionen in den sechs Teilabschnitten der Kontaktkurve wieder.
Dies wiederhlt sich dann bei den anschließenden Bildern für die Exponenten 6, 3, 2 und 1.

Der rote Geschwindigkeits-Vektor zeigt die Geschwindigkeit von K relativ zur Kontaktkurve an
und der schwarz-weiße Pfeil nach links den Vektor , wobei v die Geschwindigkeit der
schwarzen Zahnstangen-Kurve ist. Nach dem Verzahnungsgesetz muss die Summe beider Vektoren
senkrecht zur Geraden WK stehen.

In dem Abschnitt 1 zwischen W und A sei die Kontaktkurve durch das Funktionspaar (x(t) ; y(t))
mit einem Zeit-Parameter t gegeben. Dann ist . v(t) sei die Geschwindigkeit der
Zahnstangen-Kurve in Abhängigkeit von t. Das Skalarprodukt des Summen-Vektors mit
dem Ortsvektor von K muss Null sein. Folglich ist , also
. Der Integralfunktionsterm mit
gibt an, wie weit sich die Zahnstangenkurve weiterbewegt bei der Bewegung des Kontaktpunktes
von W bis zum aktuellen Punkt K zur Zeit . Eine Flanke der Zahnstange wird dann durch
beschrieben, wobei das Interval von Null bis
zu dem Zeitpunkt durchläuft, an dem K den Eckpunkt A oben rechts erreicht..

Wenn die Kontaktkurve im Abschnitt 1 durch eine Potentfunktion gegeben ist und sich K so bewegt,
dass x(t) = t ist, dann ist mit und es folgt .

In der Animation wurde der Zeitparameter so gewählt, dass die Bewegung von K auf jedem Teilabschnitt
gleichförmig ist.

Die Animation zeigt, wie die Verzahnungskurven im Zusammenhang mit dem s(u)-Grafen zustande=
kommen. Gegenüber der vorhergehenden Animation ist zu bedenken, dass sich hier die Verzahnungs=
kurven nicht bewegen, wohl aber zwei der roten Kurven, die kongruent zur Kontaktkurve sind. Die
Bewegung der Zahnstangen-Kurve in der vorhergehenden Animation wird durch die entgegengesetzte
Bewegung des zugehörigen Kontaktkurven-Duplikats mit gleichen Geschwindgkeitsbeträgen ersetzt.
Die grün gezeichneten Wege auf dem Wälzkreis bzw. der Wälzgeraden sind gleich lang. Ihre Länge
stimmt mit dem grün markierten s(u)-Wert im Grafen oben links überein. Wenn man von diesem
s(u)-Wert das 5-fache der Teilung s(6) abzieht, ergibt sich der Wert des oben genannten Terms
mit , vorausgesetzt dass jeder Teilabschnitt der Kontaktkurve
von K in der Zeit 1 mit konstanter Geschwindigkeit durchlaufen wird.