Es lebe die Geometrie!

Polygon-Billard und Kachelungen

Praktische Bedeutung haben Billards nur für Rechtecke, in mathematischer Hinsicht sind auch andere
Flächen von Interesse. Dabei werden Bahnkurven (Trajektorien) der Mitte einer gedachten Billardkugel
betrachtet, die sich im Innern der Fläche geradlinig bewegt und am Rand reflektiert wird. Eine Billard-
Trajektorie ist darum ein eventuell unendlich langer Streckenzug aus gerichteten Strecken, die zumeist
unterschiedlich klang sind. Alle Eckpunkte liegen auf dem Flächenrand, eventuell mit Ausnahme des
Startpunkts und eines Zielpunkts, falls der Streckenzug endlich ist. Wir beschreiben Richtungen von
Trajektorien-Strecken mit Hilfe der Größe des Winkels bei einer Drehung der Richtung einer Rechtsachse
in die der Strecke. Wenn eine Strecke mit dem Richtungswinkel in einem Randpunkt A reflektiert wird,
dessen Tangente einen Richtungswinkel hat, dann ist der Richtungswinkel der reflektierten
Strecke. Für den entgegengesetzten Tangenten-Richtungswinkel ergibt sich das Gleiche, da wir
hier 360° mit 0° identifizieren.

Bei Polygon-Flächen stimmen die Tangenten mit den Seitengeraden überein. In den Eckpunktes eines
Polygons ist die Reflexion zunächst nicht definiert. Wir erklären jedoch auch hier eine Billard-Reflexion,
indem wir Reflexionen an benachbarten Randpunkten stetig fortsetzen. Das gelingt sinnvoll nur für Ecken
mit einem Innenwinkel kleinergleich 90°. Wir betrachten dabei eine Trajektorien-Strecke, die 'in die Ecke
hineinläuft', d. h. deren Richtungswinkel zwischen und liegt, wobei und die
Richtungswinkel der Seiten a und b sind, die vom Eckpunkt Q ausgehen. Wenn die Strecke an a oder an b
reflektiert wird, so gilt dies auch für folgende Strecken, falls die Reflexionspunkte nahe genug bei Q liegen
und der Richtungswinkel der Strecken nicht in dem Winkelfeld der Ecke zwischen und liegt. Unter
den folgenden Strecken gibt es dann eine erste, deren Richtungswinkel zwischen und liegt.
Wir definieren: Der Richtungswinkel einer Trajektorien-Strecke, die durch Reflexion einer Strecke
mit dem Richtungswinkel im Eckpunkt Q entsteht, ist dieser Winkel . Wenn die Größe des
Innenwinkels bei Q ein Teiler von 90° ist, ergibt sich . Für einen Innenwinkel von 60°
liegen und symmetrisch zur Richtung der Winkelhalbierenden des Innenwinkels.


Auf dieser Seite werden Billard-Trajektorien zu einem Polygon dargestellt, das folgende Eigenschaft hat:

Durch Hintereinanderschaltung von Spiegelungen an Seitengeraden kann das Polygon zu einer Kachelung
der ganzen Ebene ergänzt werden.

In der Pdf-Datei ' Kachelungen, die mit Nachbar-Bewegungen erzeugt werden' wird gezeigt, dass dies nur für
Rechtecke, für rechtwinklige Dreiecke mit den Winkeln 60° oder 45° und für gleichseitige Dreiecke möglich ist.

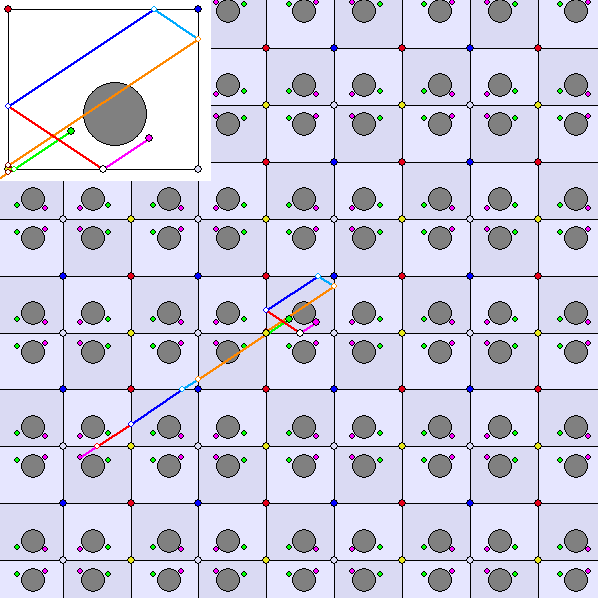
Die Gleitschau zeigt Billard-Trajektorien in einer Rechteckfläche, die am hellgrünen Punkt S starten
und den magentafarbenen Punkt Z als Ziel haben. Nur einige dieser Trajektorien vermeiden das
graue Hindernis. Welche Bahnkurven dies leisten, kann auf folgende Weise bestimmt werden:

Man ergänzt das Billiard-Rechteck durch fortgesetzte Spiegelungen an Seitengeraden zu einer
Kachelung der Ebene. Dabei werden Z und das Hindernis ebenfalls gespiegelt. Dann sucht man
eine Verbindungsstrecke von S im Billard-Rechteck mit einem der Bilder Z' von Z, die kein Bild
des Hindernisses schneidet. Die Anfangsstrecke der gesuchten Trajektorie ist dann der hellgrüne
Anfangsteil dieser Verbindungsstecke SZ'.

Die vier Seitengeraden des Billard-Rechtecks seien mit l, r, u, und o bezeichnet (links, rechts, unten,
oben) und die zugehörigen Spiegelungen mit L, R, U und O. Eine Trajektorie, die das Hindernis meidet,
ergibt sich z. B. durch aufeinander folgende Reflexionen an l, o, r, l und u. Wenn man Z erst mit U
spiegelt, dann das Bild von Z mit L, das Bild davon mit R, weiter mit O und schließlich mit L, dann
ergibt sich Z'. Kurz wird dies durch die Gleichung Z' = ZULROL ausgedrückt. Die Reihenfolge lorlu
ist hier also zu ULROL umgedreht. Der entsprechende Zusammenhang gilt für alle Trajektorien.

Da l und r orthogonal zu u und o sind, können in einer Hintereinanderschaltung von Spiegelungen U
und O mit R und L vertauscht werden, so dass z. B. ULROL = UOLRL gilt, weil alle Bilder der
Hintereinanderschaltungen ULROL und UOLRL übereinstimmen. Das Zweierprodukt UO ergibt
eine Verschiebung in y-Richtung um die doppelte Rechteck-Höhe 2h nach oben, und entsprechend
das Produkt LR eine Verschiebung um die doppelte Rechteckbreite 2b nach rechts. Bei Vertauschen
von U und O bzw. L und R wird die Verschiebungsrichtung umgedreht. Wenn Z die Koordinaten
(x ; y) hat bei einem Koordinaten-Ursprung im Schnittpunkt von l und u, dann hat ZUOLR die
Koordinaten (x+2b ; y+2h) und ZUOLRL die Koordinaten (-(x+2b) ; y+2h).

Wenn der Richtungswinkel einer Strecke der Trajektorie ist, so hat die folgende Strecke nach der
Reflexion an u oder o den Richtungswinkel und nach der Reflexion an l oder r den
Richtungswinkel . Deshalb können bei den Strecken einer Trajektorie nur vier
verschiedene Richtungswinkel vorkommen, nämlich , , und .

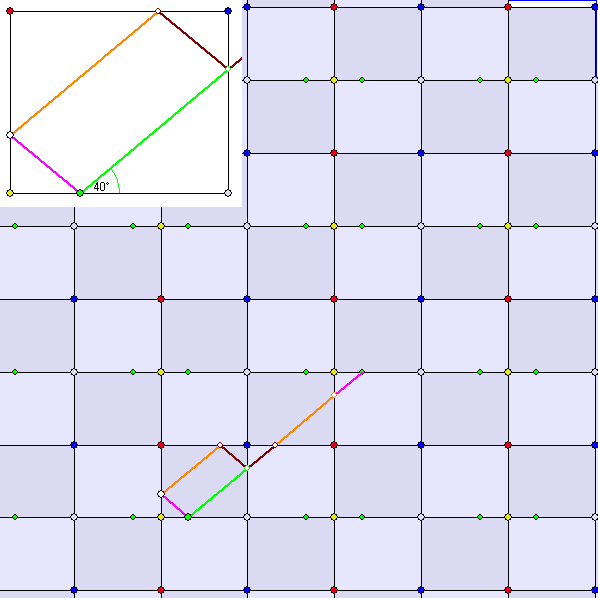
Die Gleitschau zeigt Animationen zu periodischen Billard-Trajektorien in einem Rechteck, das durch
Hintereinanderschaltungen von Spiegelungen an Seitengeraden zu einer Kachelung ergänzt wurde.
Die natürliche Zahl n ist Periode einer Billard-Trajektorie, wenn jede ihrer orientierten Strecken
mit ihrem Nachfolger n Strecken weiter übereinstimmt. Durch jeden Punkt S des Rechtecks gehen
abzählbar viele periodische Trajektorien. Die möglichen Richtungen erhält man, indem man S mit einem
Punkt S' verbindet, der als Bild bei einer Translation entsteht, die Hintereinanderschaltung von
Spiegelungen an Seitengeraden des Billard-Rechtecks ist. Wenn S ein Eckpunkt ist, werden die
Trajektorien-Strecken nach einer halben Periode in umgekehrter Richtung zurückverfolgt. Der nach
einer halben Periode erreichte Punkt ist dann darum notwendig ein Eckpunkt. Bei periodischen
Trajektorien gehen wir stets von einem Rand-Punkt aus.

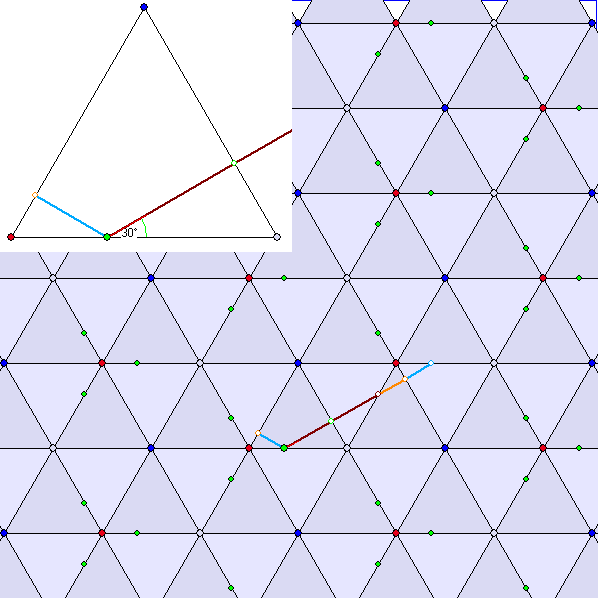
Auch bei einem gleichseitigen Dreieck als Billard-Fläche können die periodischen Trajektorien an Hand der
zugehörigen Kachelung bestimmt werden. Dazu verbindet man den grünen Startpunkt S mit entsprechenden
Punkten S' in Dreiecken, die durch eine Translation aus dem Billard-Dreieck entstehen, wobei diese
Translation sich als Hintereinanderschaltung von Spiegelungen an Seitengeraden des Billard-Dreiecks ergibt.
Die Eckpunkt-Färbung macht erkennbar, welche Dreiecke durch derartige Translationen auseinander
hervorgehen. Wenn eine Trajektorie durch einen Eckpunkt geht, dann bedeutet die Reflexion hier hinsichtlich
der Richtung eine Spiegelung an einer Winkelhalbierenden. Wenn der Richtungswinkel der Trajektorie in
S ist, dann sind , und die möglichen folgenden Richtungen.

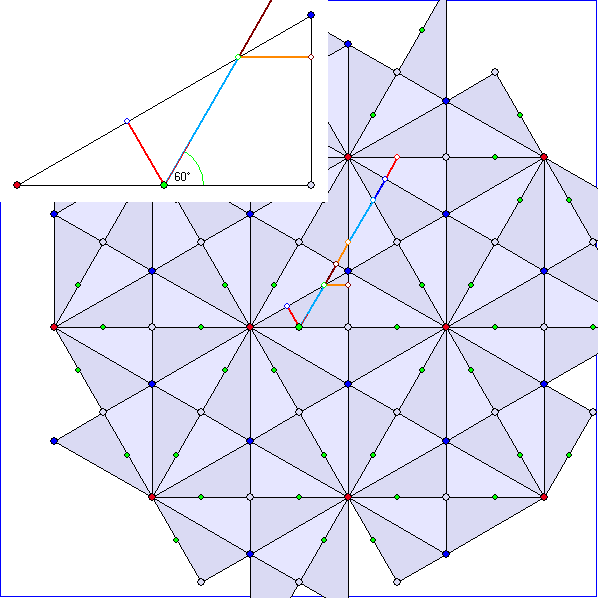
Beim rechtwinkligen Dreieck mit einem Winkel der Größe 30° bedeutet die Reflexion in allen
Eckpunkten, dass die im Eckpunkt auftreffende Strecke nach der Reflexion in umgekehrter Richtung
zurückverfolgt wird. Bei periodische Trajektorien wird darum dann nach einer halben Periode der
gleiche Weg zurückverfolgt. Das gilt auch, wenn eine Seite senkrecht getroffen wird. Es sind zwölf
Richtungswinkel möglich, nämlich ,, , und .

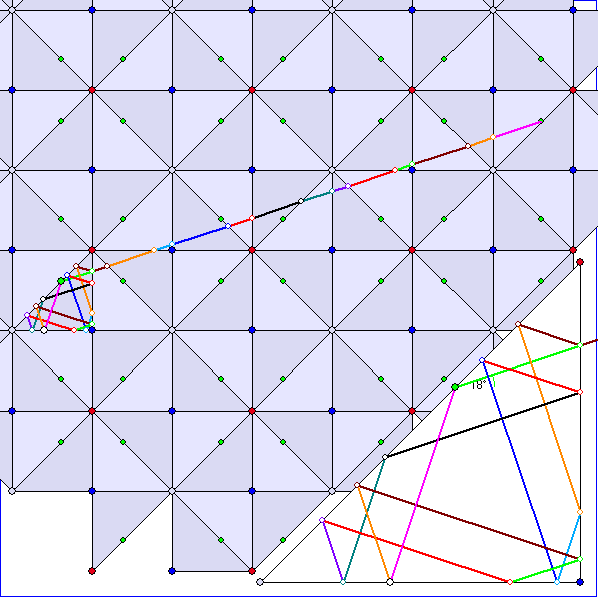
Das gleichschenklig rechtwinklige Dreieck ist die vierte und letzte Möglichkeit, eine Kachelung der
Ebene durch fortgesetzte Spiegelung an den Polygon-Seiten zu erzeugen. Bei den periodischen Billard-
Trajektorien, die sich damit ergeben, sind die Richtungswinkel , , und
möglich. Die Reflexion in den Eckpunkte wirft die Trajektorien-Strecken in sich zurück.