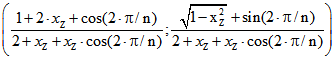Es lebe die Geometrie!
Hauptmenü
- Home
- Geometrie 1
- Geometrie 2
- Epizykeltheorie
nicht-euklidisch
Geometrie 2 > Satz von Poncelet
Satz von Poncelet (nicht-euklidisch)
--> Bewegungen auf dem Kreis und der Satz von Poncelet
(https://vivat-geo.de/Pdf-Dateien/Poncelet.pdf)
--> Die Preudosphäre und die hyperbolische Geometrie
(https://www.vivat-geo.de/Pdf-Dateien/Hyperbolische Geometrie.pdf)





Der gelbe Punkt P und der orangefarbene Punkt Q bewegen sich auf dem Einheitskreis mit einer
Geschwindigkeit v(a), die nur vom jeweiligen Ort (cos(a) ; sin(a)) abhängt, an dem sich P oder Q
befinden. Hier ist v(a) proportional zum nicht-euklidischen Abstand ![]()
des Punktes (cos(a) ; sin(a)) vom weißen Punkt ![]() . Der Abstand zwischen P und Q wurde
. Der Abstand zwischen P und Q wurde
so gewählt, dass die Zeit ![]() für den Weg von dem Ort
für den Weg von dem Ort ![]() zum Ort
zum Ort ![]() zu irgendeinem Zeitpunkt
zu irgendeinem Zeitpunkt ![]() stets
stets![]() bzw.
bzw. ![]() beträgt, wobei T die Zeit für einen Umlauf ist. Der grau gezeichnete Balken im
beträgt, wobei T die Zeit für einen Umlauf ist. Der grau gezeichnete Balken im
Graphen von der Zeit t hat also die Breite ![]() bzw.
bzw. ![]() Darum lässt sich die Strecke PQ zu
Darum lässt sich die Strecke PQ zu
einem Sehnen-Tangenten-n-m-Eck mit n = 5 bzw. n = 20 und m = 2 bzw. m = 9 ergänzen.
Die eingezeichneten Spurkreise gehören zu Zeitintervallen ![]() , mit k = 2, 3, ..., 9.
, mit k = 2, 3, ..., 9.





Das erste Bild der Animation zeigt den schwarzen Einheits-Kreis K um den Koordinaten-Ursprung N und
darauf Eckpunkte eines Dreiecks, dessen Seiten die rote Ellipse H berühren. H ist die Hüllkurve der
Seitengeraden, wenn jeder Eckpunkte sich mit der Geschwindigkeit ![]() bewegt, die
bewegt, die
zu seinem Ort ![]() gehört. Hier ist die Geschwindigkeits-Funktion
gehört. Hier ist die Geschwindigkeits-Funktion ![]()
proportional zum Abstand des Eckpunktes von der parallel zur Hochachse gezeichneten grünen Geraden
![]() , wobei
, wobei ![]() die Abszisse des grünen Punktes Z im Innern von K ist. g ist die Polare von Z
die Abszisse des grünen Punktes Z im Innern von K ist. g ist die Polare von Z
bezüglich K. H ergibt sich als Bild eines euklidischen Kreises um den Ursprung bei der hyperbolischen
Verschiebung, die N in Z abbildet, wenn man das Beltrami-Klein-Modell der hyperbolischen Ebene zu
Grunde legt. In diesem Modell werden nur die Punkte im Innern des Einheitskreises als Punkte des Modells
betrachtet und nur die Sehnen als Geraden. Man kann dazu einen nicht-euklidischen Abstand definieren, so
dass alle Axiome der euklidischen Geometrie gelten mit Ausnahme des Parallelen-Axioms. Für diesen
nicht-euklidischen Abstand ist H ein hyperbolischer Kreis, das heißt, dass alle Punkte auf H von Z den
gleichen hyperbolischen Abstand haben. Dieser Abstand ist in der Animation rot angegeben. Er ist anders
definiert als der Abstand bei den Ellipsen im oberen Bild. Die hyperbolischen Kreise des Beltrami-Klein-
Modells ergeben sich auch dadurch, dass man euklidischen Kreise auf der Halbkugel über K senkrecht auf
die Ebene von K projizieren. Siehe dazu die oben angegebene Pdf-Datei zur hyperbolischen Geometrie.
In der Animation wird zunächst der hyperbolische Kreis H um Z, der sich als Hüllkurve des Sehnen-
Tangenten-3-Ecks ergibt, durch hyperbolische Translationen bis N und wieder zurück verschoben. Dabei
bleibt K unverändert und auch der hyperbolische Radius sowie der grau eingezeichnete hyperbolische
Sehnen-Tangenten-Winkel undder hyperbolische halbe Mittelpunkts-Winkel bei Z. Im euklidischen Kreis
K um N ist das graue Sehnen-3-Eck euklidisch regelmäßig, darum sind alle Sehnen-Tangenten-Winkel
und Seitenlängen gleich groß, nämlich ![]() bzw.
bzw. ![]() . Die rote Hüll-Kurve H ist ein Kreis mit dem
. Die rote Hüll-Kurve H ist ein Kreis mit dem
euklidischen Radius ![]() und der hellblaue Polar-Kegelschnitt J ein Kreis mit dem euklidischen
und der hellblaue Polar-Kegelschnitt J ein Kreis mit dem euklidischen
Radius ![]() . Beim Rückweg verändern sich die euklidischen Größen, nicht aber die hyperbolischen. Dabei
. Beim Rückweg verändern sich die euklidischen Größen, nicht aber die hyperbolischen. Dabei
ist bemerkenswert, dass der graue halbe Mittelpunkts-Winkel nicht mit dem Sehnen-Tangenten-Winkel
übereinstimmt, im Unterschied zur euklidischen Geometrie.
Im zweiten Teil der Animation wird die Erzeugung der Hüllkurve H für n gleich 3, 4 und 5 dargestellt, für n=3
auch mit Geschwindigkeits-Vektoren an Eckpunkten des Sehnen-Tangenten-n-Ecks E. Dabei wird neben H
auch die hellblaue Pol-Kurve J gezeichnet, die sich als Spur der Pole der Seiten-Geraden von E ergibt.
Wenn P und Q aufeinander folgende Eckpunkte auf K sind, die H in B berühren, dann ist der Schnittpunkt B'
der Tangenten in P und Q kollinear mit B und Z. Alle Sehnen des Beltrami-Klein-Modells, die hyperbolisch
orthogonal zu PQ sind, liegen auf einer Geraden durch B'. Wir nennen nennt B' 'polar' zu B und
J 'Polar-Kegelschnitt' von H.
Das am Berührpunkt einer Tangente an H gau angegebene hyperbolischen Maß des Sehnen-Tangenten-Winkels
ist für alle Berührpunkte bei vorgegebener Eckenzahl gleich. Entsprechendes gilt auch für den grauen halben
Mittelpunkts-Winkel bei Z Diese Gleichheit wird in einem Mess-Verfahren mit Hilfe der grünen Geraden g und
dem Maßpunkt M auf der Rechtsachse am rechten Rand des Bildes erkennbar. M mit der Abszisse
 ist einer der beiden Punkte zu den Null-Kreisen des von K und g erzeugten Kreis-Büschels.
ist einer der beiden Punkte zu den Null-Kreisen des von K und g erzeugten Kreis-Büschels.
Wenn die Tangente an H in B die Gerade g in C schneidet und eine der beiden Sekanten-Geraden durch B den
Schnittpunkt D mit g hat, dann wird der Winkel dazwischen durch die euklidische Größe des Winkels CMD
vermessen. Diese Winkel haben das euklidische Maß ![]() . Außerdem: Wenn C1 und C2 die Schnittpunkte
. Außerdem: Wenn C1 und C2 die Schnittpunkte
der Tangenten an H in aufeiander folgenden Berührpunkten B1 und B2 auf H sind, dann hat der Winkel C1MC2
das euklidische Maß ![]() . Hierbei unterscheiden sich zwar die hyperbolischen und euklidischen Maße, aber die
. Hierbei unterscheiden sich zwar die hyperbolischen und euklidischen Maße, aber die
Gleichheit der hyperbolischen Maße wird in der Übereinstimmung der euklidischen Maße erkennbar.
Überraschender Weise stimmt das hyperbolische Maß der halben Mittelpunkts-Winkel bei Z sogar
mit den bei M gemessenen euklidischen Werten überein.
Im letzten Teil der Animation wird jeder Eckpunkt auf K von einem Zentrum V auf K aus auf die Gerade g
projiziert und die Bildpunkte mit M verbunden. Aufeinander folgende Verbindungs-Geraden schließen
dann bei M einen Winkel mit dem euklidischen Maß ![]() ein. Wenn auf K ein Eckpunkt von E und die
ein. Wenn auf K ein Eckpunkt von E und die
Maß-Gerade g gegeben ist, kann man also mit Hilfe der Winkel bei M alle anderen Eckpunkte mit Zirkel und
Lineal konstruieren und dazu alle Berührpunkte.





Das erste Bild der Animation zeigt in schwarzen Einheits-Kreis K ein Tangenten-3-Eck E der roten Hüllkurve
H. Die hellblauen Pole der Seitengeraden sind Mittelpunkte der schwarzen Kreise, die K euklidisch orthogonal
schneiden und sich in den Eck-Punkten von E berühren. Wir nennen sie 'Steiner-Kreise' nach Jakob Steiner
(1796-1863). Ihre Kreisbögen im Innern von Kergeben sich daraus, dass auf die Punkte (x;y) von E die Abbildung ![]()
angewandt wird und auf ihre Kreisbögen außerhalb von K die entsprechende Abbildung ![]() mit einem Minus-
mit einem Minus-
Zeichen vor der Wurzel. Die Abbildungen werden unten auf dieser Seite erklärt.
Die beiden blauen Kurven sind euklidischen Kreise, die aus dem roten hyperbolischen Kreis H durch
Anwendung von ![]() und
und ![]() entstehen. Sie berühren darum alle drei Steiner-Kreise. Wir nennen sie
entstehen. Sie berühren darum alle drei Steiner-Kreise. Wir nennen sie
'Rahmen-Kreise'. Sie haben ihren Mittelpunkt in den beiden Brennpunkten des hellblauen Polar-Kegelschnitts
J zu H und gehen durch Spiegelung an K auseinander hervor. Sie gehören zu dem von K und g erzeugten
Kreis-Büschel KB, zu dem der Maß-Punkt M 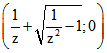 und sein Spiegel-Bild M*
und sein Spiegel-Bild M*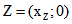
die Null-Kreise sind.
Das hyperbolische Zentrum![]() von H und die Maß-Gerade g
von H und die Maß-Gerade g ![]() sind hellgrün eingezeichnet.
sind hellgrün eingezeichnet.
Wir nennen die magenta-farbenen Kreise 'Maß-Kreise'. Jeder Maß-Kreis D hat folgende Eigenschaften :
D hat den Mittelpunkt im Schnittpunkt von g mit einer der blauen Seiten-Geraden d des Dreiecks F der
Pole der Seiten-Geraden von E und inzidiert mit dem Maß-Punkt M und mit M*. D schneidet darum alle
Kreise des Büschels KB euklidisch orthogonal.
D inzidiert mit dem Eckpunkt P von E, der auf d liegt, und berührt dort die beiden Steiner-Kreise durch P.
D schneidet jeden der beiden benachbarten Maß-Kreise unter einem Winkel mit dem euklidischen Maß 60°.
Mit Hilfe dieser letzten Eigenschaft kann man auch hier alle Eckpunkte von E mit Zirkel und Lineal konstruieren,
wenn der Einheits-Kreis K mit einem Eckpunkt darauf zusammen mit der Maß-Geraden g gegeben ist. Damit
ergibt sich auch die ganze Kette der Steiner-Kreise mit den beiden Rahmen-Kreisen.
Wie in der vorhergehenden Animation wird im ersten Teil Z hyperbolisch in das Zentrum N von K verschoben,
wodurch E zu einem regelmäßigen Dreieck wird und H zu einem euklidischen Kreis. Auf die schwarzen
Steiner-Kreise, die blauen Rahmen-Kreise und die magenta-farbenen Maß-Kreise wird die hyperbolische
Verschiebung nicht angewandt. Die Steiner-Kreise und die Rahmen-Kreise entstehen in jedem Bild durch
Anwendung der Abbildungen ![]() auf die Punkte von E bzw. H. Die Maß-Kreise bewahren in jedem Bild die
auf die Punkte von E bzw. H. Die Maß-Kreise bewahren in jedem Bild die
oben angegebenen Eigenschaften. Für Z = N werden sie zu Geraden durch N.
Nach dem Zurück-Schieben wird E auf K weiterbewegt. Dabei sind stets alle Seiten-Geraden von E Tangenten
von H und alle ihre Pole inzidieren mit J. Obwohl sich die Form des Dreiecks verändert, bleiben die Steiner-
Kreise in Berührung mit den beiden unveränderten blauen Rahmen-Kreisen. Eine derartige zyklisch geschlossene
Kette von Kreisen, die den Vorgänger und den Nachfolgen berühren und sich zwischen zwei konstanten
Rahmen-Kreisen berührend weiterbewegen können, wird Steiner-Kette genannt.
Nach der Steiner Kette mit drei Kreisen werden Steiner-Ketten mit 4 und 5 Kreisen dargestellt. Bei vier Kreisen
mit ![]() ist einer der Rahmen-Kreise die Maß-Gerade, die man als Kreis mit unendlich großem Radius
ist einer der Rahmen-Kreise die Maß-Gerade, die man als Kreis mit unendlich großem Radius
deuten kann. Der Polar-Kegelschnitt J ist dann eine Parabel mit der Maß-Geraden als Leitgerade.
Die Stand-Bilder in der Gleitschau zeigen nach der Animation auch eine Steiner-Kette zu fünf Kreisen mit der
Überschlagungs-Zahl 2, was dazu führt, dass die überschlagenden Kreise sich wie die Seiten von E schneiden.
In den letzten 18 Bildern wird für die Anzahl n gleich 3, 4 und 5 der Steiner-Kreise bei der Überschlagungs-
Zahl 1 gezeigt, dass die Bild-Punkte der Eck-Punkte von E bei hyperbolischer Spiegelung an M* ein
regelmäßiges n-Eck mit dem Ursprung als Zentrum bilden. Das Gleiche gilt für die Pole auf J.





Diese Animation zeigt eine Kette sich berührender schwarzer Kreise zwischen zwei blauen Rahmen-Kreisen,
wobei diese Rahmen-Kreise sich anders als in der vorangehenden Gleitschau ebenfalls berühren. Die Kette
wird nach Pappos von Alexandria benannt, der um 300 lebte. Während die Steiner-Kette sich stets mit nur
endlich vielen Kreise zyklisch schließt, hat die Pappos-Kette immer unendlich viele Kreise und ist nie
geschlossen. Die Pappos-Kette gibt es zu zwei berührenden Rahmen-Kreisen mit jedem Zentrums-Abstand
größer als Null, und sie ist in diesem Rahmen auch stets verschiebbar. Insofern passt sie eigentlich nicht zum
Satz von Poncelet. Sie wird aber hier wegen der Ähnlichkeiten mit der Steiner-Kette dargestellt.
Das erste Bild der Animation zeigt zu einer Pappos-Kette die beiden blauen Rahmen-Kreise, die sich im
hellgrünen Punkt Z (-1;0) berühren. Die Berührpunkte der Pappos-Kreise liegen auf dem Einheits-Kreis K
um den schwarzen Koordinaten-Ursprung N(0;0) und bilden mit den Verbindungs-Strecken der Nachbar-
Punkte das schwarze Unendlich-Eck E. Als Radius des inneren Rahmen-Kreises wurde ![]() gewählt.
gewählt.
Dann ist der Radius des äußeren Rahmen-Kreises der Kehrwert davon, da die beiden Kreise auch hier durch
Spiegelung an K auseinander hervorgehen. Die Eckpunkte des blauen Tangenten-Ecks zu E sind die Pole
der Seiten-Geraden von E bezüglich K. Sie liegen auf der hellblauen Pol-Kurve, die stets ein Kegelschnitt ist
mit den Zentren der Rahmen-Kreise als Brenn-Punkte. Die roten Schnittpunkte der Seiten-Geraden von E
mit den Geraden durch Z und den Polen der Seiten-Geraden sind die Berührpunkte der roten Hüll-Kurve H,
die sich ergibt, wenn sich E mit den Kreisen auf K weiterbewegt. Sie ist stets eine Ellipse. Der an den gelben
bzw. den roten Berühr-Punkt des Pappos-Kreises P1 angeheftete grüne bzw. rote Pfeile gehört zu der
Geschwindigkeit, die diesem Punkt auf K zugeordnet ist. Die Zerlegung in die gelben Komponenten
verdeutlichen den Zusammenhang mit der Hüllkurve.
Die Kreise im rechten Teil des Bilds ergeben sich durch Spiegelung der Pappus-Kreise an dem Kreis
um Z mit dem Radius 2. Die blauen Rahmen-Kreise werden durch diese Spiegelung die Rahmen-Geraden
dieser Kreise und K zu deren Mittel-Gerade. Die durch die beiden an den Süd-Polen zweier dieser Kreise
angehefteten Vektoren geben eine konstante Geschwindigkeit für die Kreise zwischen den Rahmen-Geraden
an. Wenn man diese Bewegung durch Projektion mit dem Zentrum Z auf K überträgt, ergibt sich für die
Punkte ![]() auf K eine Geschwindigkeit v proportional zum Abstand von P zu der hellgrünen
auf K eine Geschwindigkeit v proportional zum Abstand von P zu der hellgrünen
Tangente g an K im Punkt Z. Es ist also ![]() .Daraus ergibt sich als Zeit, die benötigt wird, um
.Daraus ergibt sich als Zeit, die benötigt wird, um
bei den vorgeschiebenen Geschwindigkeiten auf K vom Punkt (1;0) nach ![]() zu gelangen,
zu gelangen,
zu ![]() . Der Punkt Z wird also nie erreicht.
. Der Punkt Z wird also nie erreicht.
Im ersten Teil der Animation wird die Pappus-Kette bewegt mit einem Sprung über die Singularität bei Z.
Dann wird das Ausgangbild mit ![]() nach rechts verschoben und anschließend
nach rechts verschoben und anschließend ![]() bis 0,35 verkleinert.
bis 0,35 verkleinert.
Bei ![]() wird der zweite Rahmen-Kreis zu der Tangente in Z und die Polkurve zu einer Parabel mit der
wird der zweite Rahmen-Kreis zu der Tangente in Z und die Polkurve zu einer Parabel mit der
Tangente als Leit-Gerade. Danach ist die Polkurve eine Hyperbel. Die Radien der Pappus-Kreise sind dann
nicht mehr nach oben beschränkt.
Nach der Umkehrung dieses Prozesses wird die Pappus Kette um 10 ähnliche Pappus-Ketten ergänzt, die
dadurch entstehen, dass die Hintereinanderschaltung der Spiegelungen an dem äußeren und inneren
Rahmen-Kreis zehnmal hintereinander auf die jeweils innerste Pappus-Kette angewandt wird. Hinzugefügt
sind die magenta-farbenen Kreis durch Z mit Zentrum auf g, die mindestens einen der Pappus-Kreise berühren.
Dies Bild wird für Radien ![]() zwischen 0,85 und 0,35 gezeigt.
zwischen 0,85 und 0,35 gezeigt.
Im letzten Teil der Animation wird eine Eigenschafr einer zur Geraden y = 0 symmetrischen Pappus-Kette
dargestellt, die schon Pappus bekannt war. Zu jedem Kreis P dieser Kette gibt es nämlich eine Folge von
parallel zur y-Achse verschobenen Kreisen mit Berührung von Nord- und Süd-Pol, die das Bild von P bei
Spiegelung an der x-Achse enthält.
Zum Zusammenhang zwischen euklidischen und hyperbolischen Winkel-Maßen :
Bei der algebraischen Vermessung von Winkeln in der euklidischen oder hyperbolischen Ebene geht
man vom den Koordinaten-Tripels ![]() und
und ![]() zweier schneidender Geraden
zweier schneidender Geraden
aus, auf denen genau die Punkte (x;y) mit der Gleichung ![]() bzw.
bzw. ![]()
liegen. Dazu wird eine Bilinearform ![]() definiert mit der Konstanten k, die
definiert mit der Konstanten k, die
für die hyperbolische Ebene -1 ist und 0 für die euklidische. Dann wird die Größe des Winkels zwischen g und h
mit 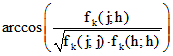 berechnet, falls diese Zahl reell ist, und andernfalls durch ihren Imaginär-Teil.
berechnet, falls diese Zahl reell ist, und andernfalls durch ihren Imaginär-Teil.
Jede Gerade durch Z kann mit einem Tripel 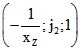 beschrieben werden. Sie schneidet die Gerade
beschrieben werden. Sie schneidet die Gerade
![]() im Punkt
im Punkt 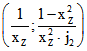 , und dessen Verbindungs-Gerade j' mit
, und dessen Verbindungs-Gerade j' mit 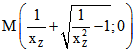 hat das
hat das
das Tripel 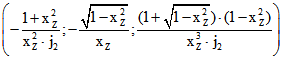 . Darum ist
. Darum ist ![]() und
und 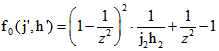
und es folgt 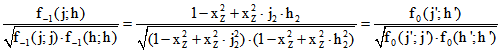 .
.
Zur Berechnung des hyperbolischen Kreises H und des Polar-Kegelschnitts J :
Wenn man die Punkte der x-y-Ebene nicht durch Koordinaten-Paare (x ; y) beschreibt, sondern durch Tripel
(x ; y; 1) in der Darstellung der projektiven Geometrie, dann ergibt sich der Bildpunkt bei der hyperbolischen
Spiegelung am Punkt (p ; 0 ; 1) durch die Abbildung S(p) :
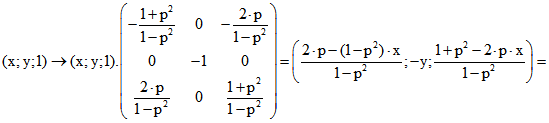
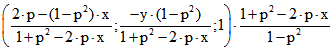 .
.
Das Koordinaten-Paar des Bildpunktes ist also 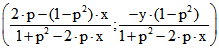 . Wenn man hier x, y
. Wenn man hier x, y
durch -x, -y ersetzt, erhält man eine hyperbolische Verschiebung S(0).S(p) längs der x-Achse. Für
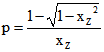 mit der Spiegelungs-Matrix
mit der Spiegelungs-Matrix 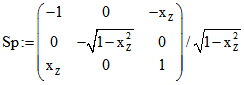 wird das hyperbolische
wird das hyperbolische
Zentrum ![]() des hyperbolischen Kreises H in den Ursprung N (0 ; 0 ; 1) gespiegelt. Der Punkt (p ; 0), an
des hyperbolischen Kreises H in den Ursprung N (0 ; 0 ; 1) gespiegelt. Der Punkt (p ; 0), an
dem gespiegelt wird, ist neben M der zweite Punkt M* der beiden Null-Kreise im von K und der Maß-Geraden
g erzeiugten Kreis-Büschel. Da die Verkettung einer Spiegelung mit sich selbst die identische Abbildung ist, wird
N durch S in das hyperbolische Zentrum Z von H abgebildet und jeder Kreis mit Zentrum N in einen Kreis mit
dem Zentrum Z. Der Bild- und der Urbild-Kreis sind hyperbolische Kreise. Der Kreis um N ist auch euklidischer
Kreis, hat also die Gleichung ![]() . Der hyperbolischer Radius r für den hyperbolischer Urbild- und
. Der hyperbolischer Radius r für den hyperbolischer Urbild- und
den Bild-Kreis ist verschieden von ![]() . Wenn es ein Sehnen-n-Eck E des Einheits-Kreises K gibt, das Tangente-
. Wenn es ein Sehnen-n-Eck E des Einheits-Kreises K gibt, das Tangente-
n-Eck eines Kreises um N mit dem euklidischen Radius ![]() ist, dann ist
ist, dann ist ![]() bei der Überschlagungs-
bei der Überschlagungs-
Zahl m und der hyperbolische Radius ![]() Zur
Zur
Berechnung siehe Satz 24 des oben angegebenen Textes zur hyperbolischen Geometrie.Wenn E den Eckpunkt![]() hat, dann ist der i-te Eckpunkt
hat, dann ist der i-te Eckpunkt ![]() , der Berührpunkt der
, der Berührpunkt der
Tangente ![]() auf dem Kreis um N ist
auf dem Kreis um N ist
![]() und die
und die
i-te Sekante ![]() . Der euklidische Sehnen-Tangenten-Winkel zwischen
. Der euklidische Sehnen-Tangenten-Winkel zwischen ![]() und
und ![]() ist dann
ist dann ![]() ,
,
unterscheidet sich aber auch von dem hyperbolischen Winkel-Maß 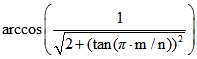 .
.
Bei den hyperbolischen Spiegelungen bleiben die hyperbolischen Maße erhalten, nicht aber die euklidischen.
Darum ist es merkwürdig, dass man das euklidische Maß beim Kreis um N nach der Spiegelung mit Hilfe
der Polaren g von Z als Maß-Gerade am Maßpunkt M ablesen kann.
Wenn ![]() Koordinaten-Paar eines Punktes von H ist, dann ist
Koordinaten-Paar eines Punktes von H ist, dann ist 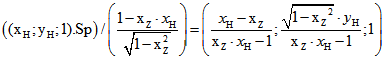 projektives Tripel eines Punktes vom Kreis
projektives Tripel eines Punktes vom Kreis
um N mit dem euklidischen Radius ![]() , und umgekehrt. Setzt man also die ersten beiden Komponenten des
, und umgekehrt. Setzt man also die ersten beiden Komponenten des
Tripels für x und y in ![]() ein, so ergibt sich eine Gleichung von H, nämlich
ein, so ergibt sich eine Gleichung von H, nämlich![]() . Diese Gleichung ist für
. Diese Gleichung ist für
![]() ,
, ![]() und
und 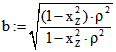 äquivalent mit
äquivalent mit ![]() .
.
Die Gleichung des Polar-Kegelschnitts ergibt sich , wenn man ![]() durch den Kehrwert ersetzt und
durch den Kehrwert ersetzt und ![]()
durch ![]() , denn der Polar-Kegelschnitt eines euklidischen Kreises um N mit dem Radius
, denn der Polar-Kegelschnitt eines euklidischen Kreises um N mit dem Radius ![]() ist ein
ist ein
euklidischer Kreis mit dem Kehrwert als Radius. Der hyperbolische Radius diese Kreises ist -r. Für![]() ist der Polar-Kegelschnitt die Parabel
ist der Polar-Kegelschnitt die Parabel ![]() , für
, für ![]() eine Ellipse und sonst eine
eine Ellipse und sonst eine
Hyperbel.
Es gibt noch eine weitere Möglichkeit, H mit einem euklidischen Kreis zu bestimmen. Dazu ergänzt man den
Einheits-Kreis K zu einer Halbkugel. Im dreidimensionalen kartesischen Koordinaten-System hat dann der Punkt
S mit den Koordinaten![]() bei senkrechter Projektion auf die x-y-Ebene als Bild den hyperbolischen
bei senkrechter Projektion auf die x-y-Ebene als Bild den hyperbolischen
Mittelpunkt von H. Die Ebene, welche die Halbkugel in S berührt schneidet die x-y-Ebene in der grünen Maß-
Geraden g. Die Schnitt-Kreise der Ebenen E durch g mit der Halbkugel haben im Halbkugel-Modell der
hyperbolischen Geometrie das Zentrum S. Die senkrechten Projektionen dieser Kreise auf die x-y-Ebene
sind hyperbolische Kreise im Beltrami-Klein-Modell mit dem Zentrum Z. Dabei ist der hyperbolische
Radius dieses Bildes bei senkrechter Projektion gleich r, wenn E das Quadrupel 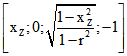 ist.
ist.
Die oben definierte Abbildung ![]() kommt dadurch zustande, dass man
kommt dadurch zustande, dass man
den Punkt (x;y) im Innern von K zunächst senkrecht in den Punkt ![]() auf der Halkugel-Fläche
auf der Halkugel-Fläche
projiziert und diesen dann zentral mit dem Zentrum (0:0:-1) auf die x-y-Ebene. Diese zweite Projektion ist eine
stereografische, bei der euklidische Kreise auf der Kugel in euklidische Kreise auf der Ebene abgebildet werden.![]() ergibt sich, wenn man den Südpol (0;0;-1) durch den Nordpol (0;0;1) ersetzt.
ergibt sich, wenn man den Südpol (0;0;-1) durch den Nordpol (0;0;1) ersetzt.
Siehe dazu die Seite ' Kreise im Halbkugel-Modell'.
Zum Zusammenhang mit der Geschwindigkeit auf dem Einheits-Kreis K :
Sei ![]() . Aus
. Aus ![]() folgt
folgt
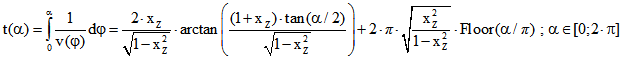 .
.
Für ![]() ist
ist 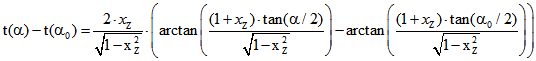 .
.
Die Zeit T für eine Periode ist 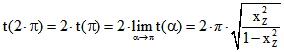 .
.
Der auf den Eck-Punkt ![]() auf K folgende k-te Eckpunkt
auf K folgende k-te Eckpunkt ![]() hat für
hat für
![]() als Winkel die Lösung der Gleichung
als Winkel die Lösung der Gleichung 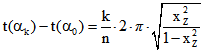 , nämlich
, nämlich
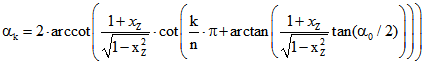 .
.
Der Berührpunkt der Tangente zwischen dem 0-ten und 1-ten Eckpunkt hat darum bei der Überschlagungszahl 1
die Koordinaten ![]() .
.
Für ![]() ergibt sich
ergibt sich