Es lebe die Geometrie!

n-Phil und [-k;+k}-Zykloide

Ein n-Phil ist eine geschlossene differenzierbare Kurve K in der Ebene mit folgender Eigenschaft:
Jedes Tangenten-n-Eck, bei dem alle Winkel zwischen aufeinanderfolgenden Seiten die gleiche
Größe 180°-360°/n haben, ist regelmäßig, und die Seiten sind für alle diese Tangenten-n-Ecke
gleich lang. K lässt sich folglich so drehen (mit möglicherweise variablen Drehpunkt), dass dabei
stets alle Seitengeraden des n-Phils berührt werden. Dabei liegt das n-Phil nicht notwendig im
Innern des n-Ecks.

In der folgenden Slideshow werden Beispiele von n-Philen angegeben, die Spitzen-Evolventen
von {-k;+k}-Zykloiden sind. Da hier nur Evolventen durch die Spitzen der Zykloiden betrachtet
werden, liegt das n-Phil stets im Innern des n-Ecks.

Begründung für die Konstruktion von n-Philen mit Zykloiden

Die k-Zykloide mit ist in der komplexen Ebene der Graph der Funktion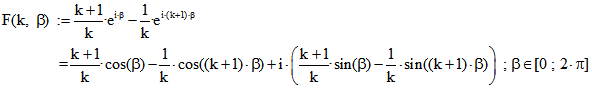

Wenn der Winkel proportional zur Zeit wächst, ist dies die Beschreibung für die Überlagerung
zweier gleichmäßiger Kreisbewegungen, bei denen sich die Radien umgekehrt zu den Beträgen
der Winkelgeschwindigkeiten verhalten.
Dies gilt auch für die zugehörige {-k;+k}-Zykloide mit dem Funktionsterm

Die Evolvente durch die Spitzen der {-k;+k}-Zykloide hat den Funktionsterm

Diese Evolvente ist also keine Zykloide, da hier drei (statt zwei) gleichförmige Kreisbewegungen
überlagert werde. Wenn man den letzten Summanden weglässt, erhält man die Evolvente durch
die Bogenmitten der {-k;+k}-Zykloide, die zu dieser ähnlich ist.



Satz1: k > 1 und n > 2 seien natürliche Zahlen, wobei n kein Teiler von k ist. Dann haben alle
Tangenten-n-Ecke der Evolvente durch die Spitzen der {-k;+k}-Zykloide, bei denen jeder
Innenwinkel zwischen aufeinanderfolgenden Seiten die Größe 180°-360°/n hat, die gleiche
Umfangslänge .

Der Beweis zu diesem Satz ergibt sich aus Satz 7 und 8 in
http://www.vivat-geo.de/Pdf-Dateien/Drehpunktfunktion.pdf.
Dort wird Graph von betrachtet. Er wird da als 1-Kurve der
Drehpunktfunktion bezeichnet. Es wird gezeigt, dass alle Tangenten-n-Ecke, bei denen jeder
Innenwinkel zwischen aufeinanderfolgenden Seiten die Größe 180°-360°/n hat, die gleiche Umfangslänge
haben. Daraus folgt Satz 1, weil sich der Graph von H aus dem von A durch folgende
Transformationen ergibt: Ersetzung von durch , Streckung mit dem Faktor und dem
Ursprung als Streckungszentrum, Verschiebung um 1/k in y-Richtung, Drehung um den Winkel
um den Ursprung. Man errechnet nämlich .

Aus Satz 1 folgt insbesondere, dass jede Evolvente durch die Spitzen einer {-k;+k}-Zykloide
ein 3-Phil (Triphil) ist, falls 3 kein Teiler von k ist.

Satz 2: k > 1 sei eine natürliche Zahlen und n = k-1 oder n = k + 1. Dann haben alle
Tangenten-n-Ecke der Evolvente durch die Spitzen der {-k;+k}-Zykloide, bei denen jeder
Innenwinkel zwischen aufeinanderfolgenden Seiten die Größe 180°-360°/n hat, die gleiche
Seitenlänge .
Die Evolvente ist dann also ein n-Phil.

Beweis: Für die Ableitung von H nach errechnet man .
Darum ist Richtungswinkel der Normalen in dem zu gehörigen Punkt
.
Die Gleichung der Tangente in hessescher Normalform ist darum
,
wobei die rechte Seite der Gleichung den signierten Abstand der Tangente vom Ursprung ist.

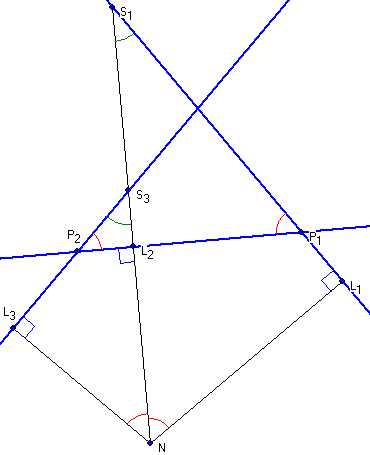
In der Zeichnung stellen die blauen Geraden drei aufeinander folgende Tangenten dar mit den
schwarz gezeichneten Loten vom Ursprung N. Die rot markieten Winkel haben die Größe
und die grün gezeichneten die Größe . Die Abstände der Lotfußpunkte
vom Ursprung seien mit bezeichnet. Dann hat die Strecke die Länge .
Wenn man diese Länge durch teilt, ergibt sich die Länge der Strecke zu .
Analog erhält man für die Strecke die Länge . Die Länge der Seite des
Tangenten-n-Ecks beträgt dann also .

sei nun der zu gehörige Punkt der Spitzen-Evolvente. Dann ist ,
und . Für
errechnet man wegen den Term
. Wenn
n = k - 1 oder n = k + 1 gilt, ist , also , so
dass der erste Summand wegfällt und sich
ergibt. Dann folgt 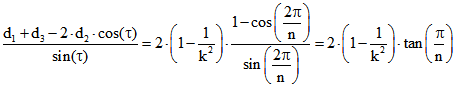.