Es lebe die Geometrie!

Euklidische Schraubungen

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum I'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum II'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_II.pdf


Eine euklidische Schraubung ist eine Abbildung der Menge der Punkte des dreidimensionalen
euklidischen Raums auf sich, die man als Hintereianderschaltung einer Drehung um eine Gerade g
und einer Verschiebung (Translation) längs g erzeugen kann. Die Vertauschung der Reihenfolge
von Drehung und Verschiebung führt zum gleichen Ergebnis, beschreibt also die gleiche Abbildung,
da diese nur durch die Zuordnung von Urbild- und Bildpunkt definiert ist. Wir nennen g die 'Achse'
der Schraubung. Jede Bewegung (Kongruenz-Abbildung), welche die Orientirung erhält, ist als
Schraubung darstellbar.

Eine Schraubung wird vollständig durch die Angabe einer orientierten Geraden g als Achse, einem
Drehwinkel und einer Verschiebungslänge bestimmt. Wir benutzen die Bezeichnung .
Den Graphen der Funktion bezeichnen wir als 'Spur der Schraubung'
oder 'Schraubungs-Bogen'.

In den folgenden zwei Gleitschauen wird die Hintereinanderschaltung zweier Schraubungen mit
verschiedenen Achsen g und h dargestellt, wobei in der ersten Gleitschau g und h parallel sind. Das
Ergebnis ist eine Schraubung, deren Achse j sich mit einer geometrischen Konstruktion aus g und h
ergibt. Der algebraische Zusammenhang zwischen g, h und j wird am Ende dieser Seite dargestellt.

Die dritte und vierte Gleitschau behandelt das Problem, bei Kenntnis der Bild-Punkte einer Schraubung
zu drei Punkten A, B und C mit einer geometrischen Konstruktion die Achse und die Schraubungs-
Parameter und zu bestimmen.

Das erste Bild der Gleitschau zeigt die orientierte rote Gerade r durch den Koordinaten-Ursprung
A = (0 ; 0 ; 0) in Richtung der z-Achse und die dazu parallelen Geraden g und b in Grün bzw. Blau.
Ihre Schnitt-Punkte A, B und C mit der x-y-Ebene sind durch Geraden c, m und y in den Farben
Cyan-blau, Magenta-rot und Gelb (Yellow) der Komplementär-Farben von Rot, Grün und Blau bei
additiver Farb-Mischung verbunden. Durch die Gleitschau soll dargestellt werden, wie sich die
Achse b der Hintereinanderschaltung von Schraubungen zu den Achsen r und g konstruieren lässt und
wie sich der Zusammenhang der gerichteten Dreh-Winkel und der signierten Verschiebungs-Längen
ergibt.

Der rote Kreisbogen im ersten Bild verbindet den Urbild-Punkt P(1 ; 0 ; 0) mit dem Bild-Punkt Q bei der
Drehung Sch(r;140°;0) von P um r gegen den Uhrzeigersinn um 140°. Der grüne Kreisbogen verbindet
Q mit dem Bild-Punkt R bei der Drehung Sch(g;160°;0) von Q um g mit dem Dreh-Winkel 160° gegen
den Uhrzeiger-Sinn. Der blaue Kreisbogen führt von P zu R durch die Drehung Sch(b;60°;0) um b mit
dem Winkel 60° im Uhrzeiger-Sinn (b ist in Richtung der negativen z-Achse orientiert).

Dieser Zusammenhang lässt sich folgendermaßen begründen: Jede Drehung um ein Gerade h kann als
Hintereinanderschaltung zweier Spiegelungen (das sind 180°-Drehungen) an zu h orthogonalen Geraden
dargestellt werden, die einen Winkel der Größe des halben Dreh-Winkels einschließen. Die Reihenfolge
der Spiegelungen bestimmt dabei den Dreh-Sinn. Darum ist Sch(r;140°;0) = S(m).S(y) die
Hintereinanderschaltung der Spiegelungen S(m) an m und S(y) an y, da die Größe des Winkels
zwischen m und y 70° ist. Analog ist Sch(g;160°;0) = S(y).S(c) . Folglich ist
Sch(r;140°;0).Sch(g;160°;0) = S(m).S(y).S(y).S(c) = S(m).S(c) = Sch(b;60°;0),
da S(y).S(y) die identische Abbildung ist, die jeden Punkt auf sich abbildet, und die Winkel-Summe im
euklidischen Dreieck 180° beträgt. Für das Bild Z := P.S(m) von P bei Spiegelung an m errechnet man
Z = P.S(m).S(y).S(y) = Q.S(y) und Z.S(c) = P.S(m).S(c) = R, also Z = R.S(c). Z ist darum gemeinsamer
Punkt der drei Kreisbögen.

In der Animation wird zunächst der Drehung Sch(r;140°;0) die Verschiebung Sch(r;0°;0,3) längs r um die
Länge 0,3 vorgeschaltet, so dass die Schraubung Sch(r;140°;0,3) entsteht. Diese Verschiebung ergibt sich
durch die Hintereinanderschaltung der Spiegelungen an zwei parallelen Geraden im Abstand 0,3, die
orthogonal zu r sind. Darum wird m um 0,15 nach unten verschoben. Das Ergebnis dieser Verschiebung
nennen wir m*. Dann ist
Sch(r;140°;0,3) = S(m*).S(m).Sch(r;140°;0) = S(m*).S(m).S(m).S(y) = S(m*).S(y).

Im zweiten Teil der Animation wird der Drehung Sch(g;160°;0) die Verschiebung Sch(g;0°;1,3) längs g um
die Länge 1,3 nachgeschaltet, so dass die Schraubung Sch(g;160°;1,3) entsteht. Dazu wird c um 0,65
nach oben im c* verschoben. Dann ist
Sch(g;160°;1,3) = Sch(g;160°;0).S(c).S(c*).=S(y).S(c).S(c).S(c*) = S(y).S(c*).
Für die Hintereinanderschaltung der Schraubungen Sch(r;140°;0,3) und Sch(g;160°;1,3) ergibt sich damit
Sch(r;140°;0,3).Sch(g;160°;1,3) = S(m*).S(y).S(y).S(c*) = S(m*).S(c*).

Da die Menge der Punkte auf der Achse einer Schraubung durch diese Schraubung auf sich abgebildet wird,
ist die Achse b dieser Hintereinanderschaltung orthogonal zu m* und c* und damit eindeutig bestimmt, da m*
und c* nicht parallel sind. Der Drehwinkel ist der Winkel 60° zwischen den Richtungs-Vektoren von m* und c*
und die signierte Verschiebungs-Länge der signierte Abstand -1,6 der Schnitt-Punkte von b mit m* und c*.
Das Minus-Vorzeichen folgt daraus, dass der Richtungs-Vektor von b nach unten gerichtet ist.

Im dritten Teil der Animation werden die Schraubungs-Parameter von Sch(r;140°;0,3) und Sch(g;160°;1,3)
proportional verkleinert, indem sie mit dem gleichen Faktor t zwischen 0 und 1 multipliziert werden. Danach
wird die Spur des Bildpunktes der Hintereinanderschaltung
als schwarze Kurve gezeichnet. Dies ist keine Spur einer Schraubung, da diese stets auf einer Zylinder-Fläche
verlaufen.

Diese Animation erweitert den Gedankengang der vorherigen auf Schraubungen mit Achsen, die
nicht parallel sind. Die Begründungen können unmittelbar übertragen werden. Zu der roten, der
grünen und der blauen Achse sind zusätzlich je acht Zahlen angegeben, welche die zugehörigen
Schraubungen mit Koordinaten beschreiben. Sie sind hier in der Form
strukturiert, wobei die Achse der Schraubung in Plücker-Koordinaten
angibt. Siehe dazu die Erklärung am Ende der Seite ' Höhen im 6-Rechteck'. Für den gerichteten
Drehwinkel und die signierte Verschiebungs-Länge gilt .
Daraus folgt , wobei und Arg die Funkrtion ist, die
der komplexen Zahl das Argument zuordnet.

Wir bezeichnen als Schraubungs-Quaternio oder als Dual-Quaternion. Zur algebraischen
Bestimmung der Achse , der Winkel-Größe und der Verschiebungs-Länge für eine Schraubungm Sch, die
sich als Hintereinanderschaltung zweier Schraubungen ergibt, kann man eine Multiplikation der zugehörigen
Quaternionen definieren, an deren Ergebnis man die Daten von Sch ablesen kann. Dies wird am Ende dieser
Seite dargestellt. Siehe dazu auch die oben angegebenen Pdf-Dateien.

Das erste Bild der Gleitschau zeigt die weiß umrandeten Punkte A und B mit den Koordinaten-
Tripeln a und b und den Bildern A* und B* mit den Tripeln a* und b* bei der Drehung
mit der Achse g, die hier mit der z-Achse zusammenfällt. Es soll dargestellt werden, wie man aus den
Daten a, b, a* und b* die zunächst unbekannte Achse und die Schraubungs-Parameter konstruieren kann.
Der rote bzw. grüne Vektor a* - a bzw. b* - b verbindet die Punkte A und A* bzw. B und B*. Die beiden
grau gefüllten blauen Vektoren sind die Verbindungs-Vektoren b - a bzw. b* - a* der Punkte A und B
bzw. a* und B*, die beide an A angesetzt wurden. Diese haben die gleich Länge, da die Schraubung
die Abstände zwischen zwei Punkten erhält. Der weiß bzw. schwarz gefüllte magenta-farbene Vektor
ist die Differenz bzw. Summe dieser Verbindungs-Vektoren, also wm: = (b* - a*) - (b - a) bzw.
sm := (b* - a*) + (b - a). wm und sm liegen in der gleichen Ebene und sind orthogonal zueinander, weil
b - a und b* - a* die gleiche Länge haben und folglich eine Raute mit wm und sm als Diagonalen-Pfeile
aufspannen.

Im ersten Teil der Animation wird B parallel zur Achse mit dem Richtungs-Vektor bis in die
u g senkrechte Ebene E durch A verschoben, in der der rote Kreis durch A und A* liegt. Der Verschiebungs-
Vektor v ist hier . Da B* dabei weiterhin das Bild von B bei der Drehung ist, wird
v auch auf B* angewandt. Da (b* - b) unverändert bleibt, gilt dies auch für wm = (b* - b) - (a* - a), so dass
wm parallel in E verschoben wird. wm ist also vor und nach der Verschiebung ein Vektor orthogonal zu g.
Dagegen ändern sich die schwarz-gefüllten blauen Vektoren auch in ihrer Richtung, da sie an A angeheftet
bleiben, und fallen jetzt mit den weiß gefüllten blauen Vektoren in der Ebene E zusammen. Auch sm ändert
sich, nicht aber , da sich nur die Komponente von sm in Richtung von g ändert.

Im zweiten Teil der Animation wird die Projektion in die Vogel-Perspektive verändert. Man erkennt dann,
dass der weiß gefüllte hellblaue Pfeil durch Drehung um aus dem dunkelblauen Pfeil entsteht.
Es ist folglich . Im dritten und vierten Teil wird der Prozess umgekehrt.

Im fünften Teil wird die Verschiebungs-Länge von 0 aud 1,30 erhöht. Auch dabei ändert sich an der
Gültigkeit der Formel nichts, denn dadurch wird weder wm noch sm
verändert. Diese Formel wird nach Olinde Rodrigues (1895-1951) benannt. Sie ist die Grundlage für
die Achsen-Bestimmung bei Kenntnis der Abbildungs-Pfeile zu drei Punkten A, B und C, für welche
die Vektoren (a* - a), (b* - b) und (c* - c) nicht linear abhängig sind.
Dies wird in der nächsten Animation dargestellt.

Die Gleitschau zeigt die Schraubungs-Spuren zu drei Punkten A, B und C, für welche die Vektoren
(a* - a), (b* - b) und (c* - c) nicht linear abhängig sind. Diese Vektoren sind in der linken Zeichnung
vom Koordinaten-Ursprung N aus verkleinert als weiß gefüllte Pfeile mit farbigem Rand abgetragen.
Die schwarz gefüllten Pfeile gehören zu den Vektoren , und
, deren Länge proportional zu den Inhalten der drei Seiten-Flächen durch N des
von (a* - a), (b* - b) und (c* - c) aufgespannten Tetraeders T sind. Der zugehörige Pfeilzug
verbindet N mit der Spitze des weiß gefüllten grauen Summen-Pfeils v. Dieser gibt die Richtung der
Höhen-Gerade durch N für das Tetraeder T an und für die Schraubung die Richtung der Achse.

Zur Begründung benutzen wir die Formel von Olinde Rodrigues mit
wm = (b* - b) - (a* - a) und sm = (b* + b) - (a* + a) und mit wm1 = (c* - c ) - ( b*- b) und
sm1 = (c* + c ) - (b* + b). Wegen und ist






Daraus ergibt sich , und aus
.

Zur Berechnung der Quaternio für die Hintereinanderschaltung zweier Schraubungen:

Wir bezeichnen mit dem Paar (a;b) reeller Zahlen und dem Paar (u;v) mit
Tripeln reeller Zahlen als Schraubungs-Quaternio oder als Dual-Quaternion auch dann,
wenn ist, also (u;v) zu keiner Geraden, sondern einem Gewinde gehört.
Wir definieren dafür folgende Verknüpfungen:

für relle Zahlen r

,
wobei z. B. .
Bei Benutzung der auf der Seite ' Höhen im 6-Rechteck' erklärten Dual-Zahlen vereinfacht sich
die Beschreibung mit den fetten Buchstaben a :=(a;b), c:=(c;d); u:=(u;v) und w:=(w;x) zu
(a;u)+(c;w):=(a+c:u+w)


gilt nur dann, wenn ist.
Dar Eins-Element ist ,das Null-Element ,
das wir ebenfalls mit 0 abkürzen.
Die Multiplikation mit dem Paar reeller Zahlen r:=(r;s) wird zusätzlich erklärt durch
, und .
Wenn man mit einer nicht-reellen Einheit rechnet, für die gilt, aber sonst alle üblichen Rechenregeln,
dann kann man jedes Paare (r;s) reeller Z/ahlen durch die duale Zahl ersetzen. Zum Beispiel ist
und


.
Zur dualen Zahl gehört die konjugierte duale Zahl ,
die Norm und für das inverse Element .
Zur Quaternio (a;u) gehört der konjugierte Quaternio (a;-u) , die Norm
und für der inverse Quaternio .

Das Quaternionen-Produkt hat leider meist nicht
eine Form, aus der man unmittelbar die Schraubungs-Achse , Winkel-Größe und Verschiebungs-Länge
ablesen kann, da das Tripel-Paar im Allgemeinen nicht zu einer Geraden, sondern
zu einem Gewinde gehört, weil ist. Man muss das Produkt darum zuerst mit dem Normierungs-Faktor
multiplzieren. Dann erst ist Tripel-Paar der

Achse des Schraubungs-Produkts und für das Tripel-Paar
. Der Richtungs-Vektor s hat dann die Länge 1.

Für die Berechnung der Bildpunkte gehen wir wie auf der Seite ' Winkelhalbierende im 6-Rechteck'
von der Plücker-Matrix 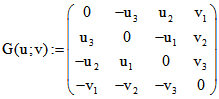für Tripel-Paare (u;v) aus, multiplizieren
aber hier die letzte Spalte nicht mit -1, sondern mit 0, da wir keine hyperbolische Raum-Geraden
betrachten, sondern euklidische. Die so modifizierte Plücker-Matrix nennen wir auch hier GS(u;v).
Zu einer Schraubungs-Quaternio definieren wir dann die Matrix
,
wobei I die Einheits-Matrix mit vier Einsen in der Haupt-Diagonalen und sonst nur Nullen ist. Die
Matrix 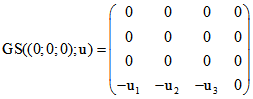nennen wir 'polar zu GS(u;v)'.
Die Detetrminante von ist .
Für alle Schraubungs-Quaternionen gilt .
Ausgehend vom Tripel eines Raumpunktes P bilden wir das zugehörige Quadrupel
. Der Bildpunkt von P bei der Schraubung zur Quaternio (a;u) hat dann das im
Allgemeiner zunächst nicht normierte Quadrupel . Wenn wir dies Quadrupel durch die
vierte Komponente teilen, erhalten wir das zugehörige normierte Quadrupel, bei dem die ersten drei
Komponenten das Tripel des Bildpunktes von P ergeben.

Dieses Verfahren führt auch dann zum richtigen Ergebnis, wenn die Quaternio der Schraubung ein
Tripel-Paare (u;v) enthält, für das ist, der Normierungs-Faktor NF(u;v) also nicht
multipliziert wurde.

.