Es lebe die Geometrie!

Satz von Poncelet (euklidisch)

--> Bewegungen auf dem Kreis und der Satz von Poncelet (https://vivat-geo.de/Pdf-Dateien/Poncelet.pdf)

Der Satz von Poncelet besagt Folgendes:
Gegeben seien zwei Kreise, von denen der eine im Innern des anderen liegt. Beginnend bei einem Punkt
des äußeren Kreises werde eine Streckenzug gezeichnet, der aus Sehnen des äußeren Kreise und aus
Tangenten des inneren Kreise besteht. Wenn der Streckenzug sich in dem Punkt schließt, dann gibt es für
jeden Anfangspunkt P auf dem äußeren Kreis einen geschlossenen Streckenzug aus Sehnen und Tangenten.

Der gelbe Punkt P und der orangefarbene Punkt Q bewegen sich auf dem Einheitskreis mit einer
Geschwindigkeit v(a), die nur vom jeweiligen Ort (cos(a) ; sin(a)) abhängt, an dem sich P oder Q
gerade befinden. Hier ist v(a) proportional zum Abstand des Punktes P bzw. Q vom schwarzen
Punkt Z (z ; 0). Es ist also mit einer Konstanten c. Die Geschwindugkeit
wird durch die Pfeile bzw. angegeben, die an P bzw. Q ansetzen. Der weiße Punkt R teilt die
Strecke PQ im Verhältnis zu mit und . Es ist also .
Daraus folgt , da wegen .
Der rot gezeichnete Geschwindigkeitspfeil zeigt genau dann in Richtung der Strecke PQ, wenn die an
R angesetzten Vektorpfeile und die gleiche Länge haben. Wegen
trifft dies zu. Der Term ist als schwarzer Pfeil eingezeichnet. Da in Richtung der Strecke PQ
zeigt, ist die Sekanten PQ stets Tangente an die rot gezeichnete Spurkurve von R. Auf Grund der hier gewählten
Geschwindigkeitsfunktion v(a) ist die Spurkurve ein Kreis Außerdem folgt aus dem Sinussatz, dass R stets
auf der Winkelhalbierenden des Winkels PZQ liegt.

Wegen der Tatsache, dass die Geschwindigkeit v(a) nur vom Ort abhängt, ist für beide Punkte P und Q
die Umlaufzeit T gleich groß (hier 6,7). und seien die Orte zu irgendeinem Zeitpunkt . Der Abstand von
P und Q ist hier so gewählt, dass die Zeit für den Durchlauf der Wegs von nach genau beträgt.
Wir nennen den 'Zeitabstand' von und . hat zur Folge, dass sich die Strecke PQ durch
zwei weitere Strecken zu dem blauen Sehnen-Tangenten-Dreieck des schwarzen und des roten Kreises
vervollständigen lässt, bei dem der Endpunkt der dritten Strecke mit P zusammenfällt.

Die beiden Funktionsgraphen zeigen die Funktionen a --> v(a) für die Geschwindigkeit und a --> t(a) für
die Zeit, die P oder Q für den Weg vom Ort (1 ; 0) zum Ort (cos(a) ; sin(a)) benötigen. t(a) ist durch das
Integral 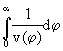bestimmt. Die Breite des grauen Balkens im Graphen von a --> t(a) gibt die Zeitdifferenz
zwischen den Orten von P und Q an. Sie ist immer gleich, nämlich .

Hier wurde der Abstand zwischen P und Q so gewählt, dass die Zeit für den Weg von dem Ort
zum Ort zu irgendeinem Zeitpunkt stets beträgt. Der grau gezeichnete Balken im
Graphen von der Zeit t hat also die Breite . Darum lässt sich die Strecke PQ zu einem
Sehnen-Tangenten-Viereck ergänzen.

Der blaue Kreis schneidet den schwarzen Einheitskreis und den roten Spurkreis von R senkrecht.
Der Mittelpunkt des blauen Kreise ist der Schnittpunkt M der Geraden PQ mit der Mittelsenkrechten
von ZR. Bei der Bewegung von P und Q wandert M auf einer Geraden. Diese ist die Mittelsenkrechte
von Z und dem Bildpunkt von Z bei Spiegelung an dem schwarzen Einheitskreis.

Hier wurde die Umlaufzeit T mit dem Faktor bzw. multipliziert, so dass sich ein Sehnen-Tangenten-
n-m-Eck mit der Eckenzahl n = 5 bzw. n = 20 und der Überschlagungszahl m = 2 bzw. m = 9 ergibt.
Außerdem sind Spurkreise mit m = 1 zu n = 3, 4, 5, 6, 7, 8, 9 und 10 eingezeichnet, die also zu Faktoren
gehören. Für jeden reellwertigen Faktor zwischen 0 und 1 gibt es einen derartigen Spurkreis von R. Aber nur
für rationale Faktoren ergibt sich ein geschlossenes Sehnen-Tangenten-Vieleck.

Nur wenn der Zeitabstand zwischen dem gelben Punkt P und dem orangefarbenen Punkt Q gleich
ist, lässt sich die Strecke PQ zu einem Sehnen-Tangenten-n-m-Eck ergänzen. In dem Fall kann P
verrückt werden, so dass der Sehnen-Tangenten-Streckenzug bei unveränderter Hüllkurve geschlossen
bleibt. (Die Form des Streckenzugs ändert sich dabei allerdings.) Dieser Sachverhalt wird hier für m = 1
und m = 2 gezeigt.

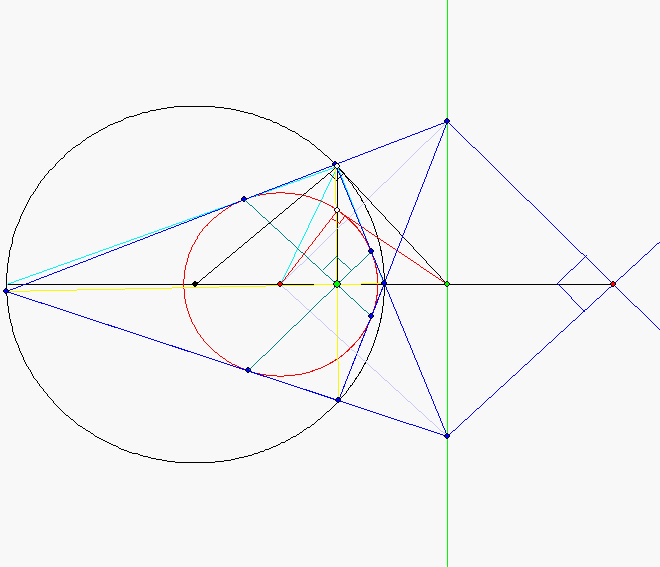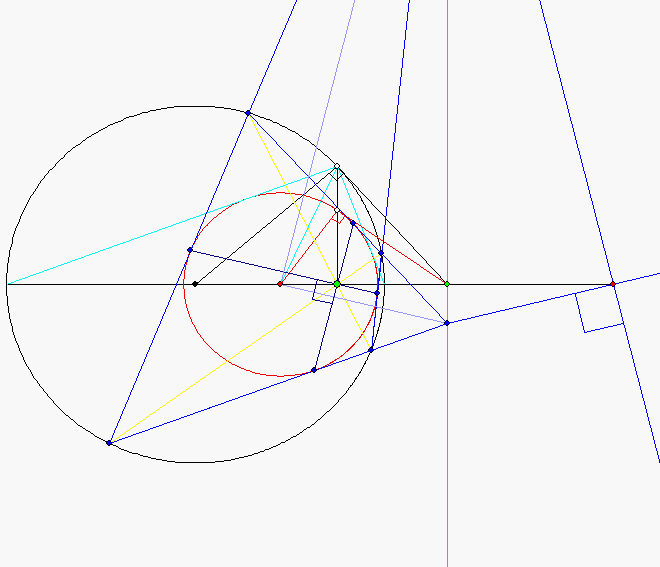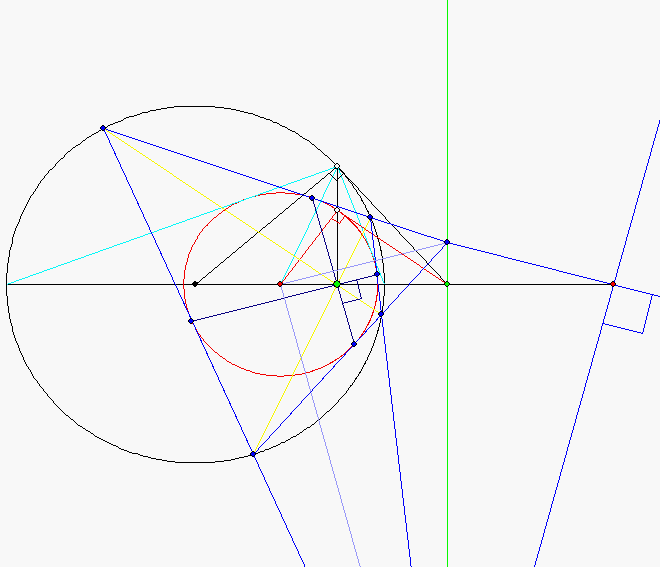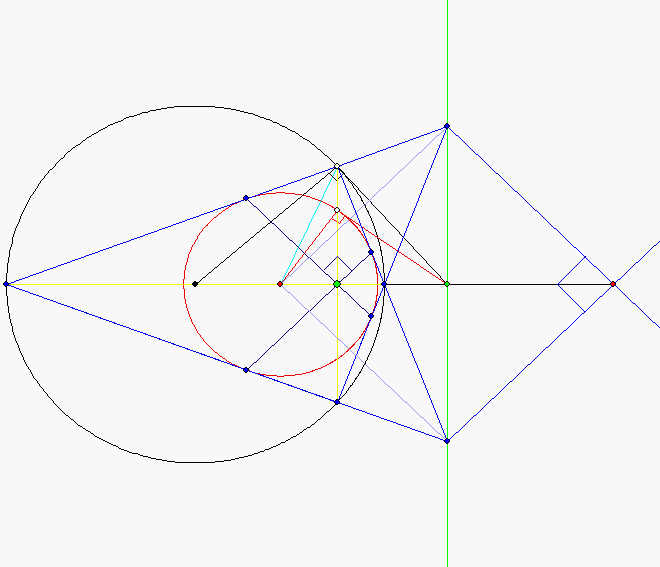
Beim euklidischen Sehnen-Tangenten-Viereck treten Besonderheiten auf, die bei anderen Eckenzahlen
fehlen. Die Größe des roten Kreises innerhalb des schwarzen Einheitskreises wird durch den hellgrünen
Punkt Z(z ; 0) bestimmt. Er ist Höhenfußpunkt in dem hellblau gezeichneten rechtwinkligen Dreieck. Die
Winkelhalbierende des rechten Winkels in diesem Dreieck schneidet die Rechtsachse in dem Mittelpunkt
U des roten Hüllkreises. Sein Radius ergibt sich als Abstand von den Katheten.
Die grüne Gerade g mit der Gleichung ist die Polare von Z sowohl bezüglich des Einheitskreises,
als auch bezüglich des roten Hüllkreises. Die beiden grünen Punkte Z und Z' gehen durch Spiegelung an
beiden Kreisen auseinander hervor. Der rote Mittelpunkt U des Hüllkreises hat den gleichen Abstand von
Z' wie der Punkt am rechten Winkel des hellblauen Dreiecks. Der rechte rote Punkt M entsteht durch
Spiegelung von U an g. Gegenüberliegende Seitengeraden des Sehnen-Tangenten-Vierecks schneiden
sich in Punkten B und C von g. Die Verbindungsgeraden von B und C mit M schneiden sich rechtwinklig.
Die Verbindungsgeraden der gegenüberliegenden Tangentenberührpunkte schneiden sich ebenfalls
rechtwinklig, und zwar in Z.