Es lebe die Geometrie!

Epizykel-Theorie bei Kopernikus, Al-Tusi und Ptolemäus
Edzard Salow

Motto: Ellipsen mittels Epizykeln,
da heißt es stückeln, stückeln, stückeln... (Bernhard Arnold)

--> Pdf-Dokument (https://www.vivat-geo.de/Pdf-Dateien/Kopernikus.pdf)

Kurz vor seinem Tode im Jahr 1543 veröffentlichte Nikolaus Kopernikus sein Hauptwerk
'De revolutionibus' [3] , aber schon 30 Jahre früher hatte er die Grundlagen seines
heliozentrischen Systems in der kleinen Schrift 'Commentariolus' [2] dargelegt. Darin
wird auch das Motiv für seine Untersuchungen deutlich. Es war nämlich nicht so, dass
er sich an Ungenauigkeiten bei der Vorhersage der Planetenbahnen nach dem 1400
Jahre lang weitgehend unangefochtenen Modell von Claudius Ptolemäus (ca. 100 bis
175 n. Chr.) störte. Auch scheint es fast so, als wäre es nicht sein Hauptanliegen gewesen,
die ihm bekannte Idee des Aristarch von Samos über die zentrale Rolle der Sonne wieder
aufzugreifen. Ihm ging es vielmehr um den mathematischen Aspekt der Rückführung
komplizierter Bewegungen auf einfache. Im ersten Absatz von [2] heißt es:

'Unsere Vorfahren nahmen am Himmel eine große Zahl von Sphären an, um die sichtbare
Bewegung der Planeten durch das Prinzip der Regelmäßigkeit zu erklären. Denn sie
fanden es völlig absurd, dass ein Himmelskörper sich nicht mit konstanter Geschwindigkeit
auf einer perfekten Kreisbahn bewegen müsste. Sie sahen, dass es möglich ist, jede
Bewegung eines Körpers durch Kombination regelmäßiger Bewegungen zu erzeugen.'

Dies ist die Leitidee der Epizykel-Theorie, die von Apollonius von Perge (262 v.Chr.
bis 190 v. Chr.) für die Planetenbahnen entwickelt wurde. Sie war Grundlage der
Astronomie des Altertums und des Mittelalters in Europa und im vorderem Orient.
Apollonius erklärte erfolgreich die Schleifenbewegungen der äußeren Planeten Mars,
Jupiter und Saturn. Wenn nämlich der Ortsvektor der Erde und der des Mars
im heliozentrischen Koordinatensystem ist, dann ist der Ortsvektor des Mars
im geozentrischen System. Nimmt man für die Planeten näherungsweise gleichförmige
Kreisbewegungen um die Sonne an, so ergibt sich bei einer Beschreibung in einem
Koordinatensystem, dessen Ursprung im Erdmittelpunkt liegt, eine Überlagerung zweier
Kreisbewegungen, die allerdings nicht in einer Ebene liegen. Da Kopernikus dieses von
Apollonius angenommene Bewegungsmodell mit seinem heliozentrischen System
überflüssig machte, erstaunt es zunächst, warum er so nachdrücklich auf der Kombination
regelmäßiger Kreisbewegungen bestand.

Manche Autoren haben Kopernikus das Beharren auf der Epizykel-Theorie als Ausdruck
einer allzu rückwärts gewandten Haltung vorgeworfen. So schreibt Arthur Koestler in
'The Sleepwalkers' ([7], III,2,4): 'Nur ein konservativer Mensch wie Kopernikus konnte
auf den Versuch verfallen, zwei unverträgliche Theorien zu versöhnen, nämlich die
Doktrinen der aristotelischen Physik und der ptolemäischen Rad-Geometrie auf der einen
Seite und der des sonnenzentrierten Universums auf der anderen.' Hierbei wird die
Tragfähigkeit der Epizykel-Theorie im Rahmen der komplexen Fourier-Analyse übersehen.
Das soll im Folgenden dargestellt werden.

Anders als in der antiken Epizykel-Theorie beschränkt man sich in der Fourier-Analyse
komplexwertiger Funktionen auf die Überlagerung von gleichförmigen Kreisbewegungen
in der Form , bei denen die Winkelgeschwindigkeiten ganzzahlige Vielfache
einer Konstanten w sind. Wenn eine natürliche Zahl n und komplexe Zahlen
gegeben sind, nennen wir die Funktion ,
(komplexwertiges) trigonometrisches Polynom zur Winkelgeschwindigkeit w. Aus dem
Approximationssatz von Stone-Weierstrass folgt dann

Satz 1 (siehe z.B. [4]). Es sei p eine stetige Funktion von der Menge R der reellen Zahlen
in die Menge C der komplexen Zahlen mit der Periode T gegeben. Zu jedem d > 0 gibt
es dann ein trigonometrisches Polynom zur Winkelgeschwindigkeit , so dass gilt:
für alle .

Jede ebene stetige Kurve p lässt sich demnach durch eine Überlagerung von gleichförmigen
Kreisbewegungen in der Form beliebig gut approximieren.
Wenn q ein trigonometrisches Polynom ist, so ist der Koeffizient der Mittelwert von q
im Periodenintervall [0,T], da für der Mittelwert jeder gleichförmigen Kreisbewegung
, gleich Null ist. Die Koeffizienten mit ganzzahligem ergeben
sich als Mittelwert der Funktionen ,. Das motiviert die folgende
Definition: p sei wie in Satz 1 gegeben. Dann heißt 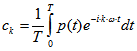k-ter Fourier-
Koeffizient zu p.

Es wäre wünschenswert, dass man sich in Satz 1 auf Fourier-Koeffizienten beschränken könnte.
Leider ist das nicht bei allen stetigen Funktionen p möglich. Es gilt aber

Satz 2 (siehe z.B. [1]): Wenn p eine stetige und stückweise stetig differenzierbare Funktion
mit der Periode T von R in C ist, dann konvergiert die Folge der trigonometrischen Polynome
mit Fourier-Koeffizienten und gleichmäßig gegen p.

Eine Planetenbahn ist nach dem 1. keplerschen Gesetz bei Vernachlässigung des störenden
Einflusses anderer Planeten eine Ellipse in einer Ebene durch die Mitte der Sonne, die im
Brennpunkt der Ellipse steht. Die Kepler-Bewegung lässt sich durch eine Funktion in der
Form , darstellen. Dabei sind die Symmetrieachsen
der Ellipse Koordinatenachsen, die große Halbachse hat die Länge 1, die kleine die Länge b ,
und die numerische Exzentrizität ist . Der Winkel E zwischen großer Halbachse
und dem Ortvektor des Planeten wird als 'exzentrische Anomalie' bezeichnet. Die Beziehung
zwischen E und der sogenannten 'mittleren Anomalie' M = stellt die Kepler-
Gleichung her. Sie folgt aus dem 2. keplerschen Gesetz. Ist ein Zeitpunkt t
gegeben und damit auch M, so kann man durch Bestimmung von E aus dieser Gleichung den
Ort eines Planeten berechnen, wenn man die Lage der Symmetrieachsen der Ellipse kennt.

Die Fourier-Koeffizienten der Kepler-Bewegung p lassen sich nach der Substitution
folgendermaßen darstellen:

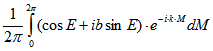mit .

In Abbildung 1 werden für eine Kepler-Bewegung auf einer Ellipse mit der numerischen
Exzentrizität 0,85 die Planetenorte für acht äquidistante Zeitpunkte bis
im Zeitabstand durch kleine Kreise angezeigt, wobei die Sonne im rechten Brennpunkt
steht. Die Pfeile mit den Nummern k = 0, 1, -1, 2 und 3 geben durch ihre Länge und Richtung
den Betrag und das Argument der komplexen Zahl wieder. Zur Zeit t = 0 sind alle
Pfeile zu nach rechts gerichtet. Die Spitze des Pfeilzugs wandert auf der Epizykel-Kurve
, die sich ergibt, wenn sich die Pfeile mit der Winkelgeschwindigkeit
drehen. In den Darstellungen der Epizykeltheorie werden üblicherweise die Pfeile durch Kreise
ersetzt, für welche die Pfeile Radius-Vektoren sind. Der größte Kreis, der zur Nummer 1, wird
als Deferent bezeichnet, die andern als Epizykeln.

Abbildung 1 zeigt, dass die Approximation der Kepler-Bewegung p durch q so schlecht ist, dass
die Sonne S außerhalb der Epizykel-Kurve liegt. Bei den Planeten unserer Sonne ist wegen der
kleineren Exzentrizität der Fehler wesentlich kleiner. Nimmt man beim Mars (e = 0,0934) die
fünf Pfeile mit den Nummern 0, 1, -1, 2 und 3, dann beträgt der Abweichungswinkel von q(t)
zu p(t) von der Erde aus gesehen maximal 3' 14''. Nimmt man noch den Pfeil mit der Nummer 4
hinzu, schrumpft der maximale Winkel auf 29''. Diese Approximation hätte auch den
Genauigkeitsmaßstäben von Kepler genügt. Denn er setzte bei der Verwertung der
Beobachtungsdaten von Tycho Brahe (1546 - 1601) einen maximalen Fehler von 2 Bogenminuten
voraus.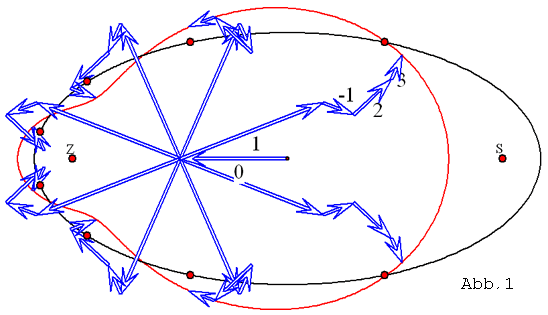

Abbildung 1 macht deutlich, dass die Spitze des Pfeils zur Nummer 0 genau in der Mitte zwischen
dem von der Sonne nicht besetzten Brennpunkt Z(-e ½ 0) und der Ellipsenmitte (0 ½ 0) liegt.
Dieser Punkt L gibt den Mittelwert der Kepler-Bewegung an; man kann ihn als den
'Schwerpunkt der Bewegung' ansehen.

Die Fourier-Koeffizienten der Kepler-Bewegung lassen sich mit Hilfe der Bessel-Funktionen
1. Art darstellen. Nach der Jacobi-Anger-Identität sind die Werte die Fourier-
Koeffizienten der Funktion . Also ist
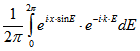und
.
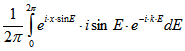Die Taylor-Entwicklung der Bessel-Funktion mit ist
,
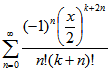und für k < 0 ist .

Satz 3 (vgl. z.B. [9]): Für die Fourier-Koeffizienten der Kepler-Bewegung gilt:
und für .

Beweis: Die Substitution ergibt

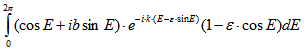
Für k = 0 folgt der Satz unmittelbar durch Ausmultiplizieren. Für wird partiell integriert:



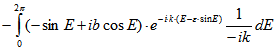
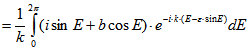
Damit errechnet man



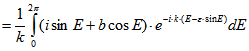
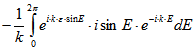
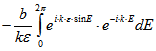
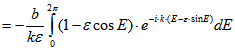
q.e.d.

Ersetzt man durch die Binomialentwicklung und vernachlässigt
e-Potenzen mit Exponenten größer als 2, so sind nach Satz 3 nur folgende Koeffizienten zu
berücksichtigen:

Wenn man nur e-Potenzen bis zur Ordnung 1 nimmt und den Koordinatenursprung in die Sonne
verlegt, erhält man die Funktion
mit
als Approximation der Kepler-Bewegung. Dieses Modell wurde von Kopernikus verwendet
und schon vor ihm im 13. Jahrhundert von den Astronomen Muayyad al-Din al-Urdi (? - 1266)
und Nasir al-Din al-Tusi (1201-1274) am Observatorium in Maragha im Nordwesten des
heutigen Iran [8]. Es hat den gleichen Bewegungsschwerpunkt wie die Kepler-Bewegung und
wie diese für e > 0 genau eine Symmetrieachse, Apsidenlinie genannt, die durch den
sonnennächsten Punkt (Perihel) und den sonnenfernsten Punkt (Aphel) der Planetenbahn geht.
Die Überlagerung K von Kreisbewegungen hatte Kopernikus in der Einleitung von [2] im Sinn,
und er hat sie in [3], V,4 detailliert ausgeführt. Er benutzte dieses Bewegungsmodell für die
Längenbewegung der Planeten, die sich wegen des nur kleinen Winkels zwischen
Planetenbahnebene und Erdbahnebene im wesentlichen dadurch ergibt, dass man die
Planetenbahn senkrecht auf die Erdbahnebene projiziert. Für die Exzentrizität e berechnete
er aus eigenen Messungen beim Saturn den Wert 0,057 ([3],V,6; moderner Messwert: 0,056)
und beim Jupiter den Wert 0,046 ([3],V,11; moderner Wert: 0,049). Allerdings wählte er
hierbei nicht den Sonnenmittelpunkt S als Ursprung, sondern den Antifokus Z der Erdbahn,
also den Brennpunkt der Kepler-Ellipse, in dem die Sonne nicht steht. Diese Merkwürdigkeit
hat bei den Planeten Saturn und Jupiter wegen ihrer großen Bahn kaum einen Einfluss, wohl
aber beim Mars. Hier errechnete er die Bewegungsfunktion
([3],V,19), wobei der heutige Messwert der Exzentrizität e = 0,093 ist.

Für die Erdbahn benutzte Kopernikus wie Ptolemäus ein anderes Bewegungsmodell, das
ursprünglich von Hipparch (190-120 v.Chr) stammt. In der heliozentrischen Umdeutung
dieses Modells wird die Bewegung der Erde um die Sonne durch
beschrieben. Dabei haben wir anders als Kopernikus die Sonnenmitte als
Koordinatenursprung gewählt, aber die Zahl 0,0323 aus [3],III,16 übernommen. Der
Term mit der doppelten Winkelgeschwindigkeit fehlt hier. 0,0323 ist ein Näherungswert
für die doppelte Exzentrizität der Erdbahn (heutiger Wert: e = 0,0167). Die Erde beschreibt
demnach eine gleichförmige Kreisbewegung um den Antifokus Z. Der Schwerpunkt dieser
Bewegung ist also weder der Mittelpunkt der Ellipse, noch der Schwerpunkt der Kepler-
Bewegung. In diesem Zusammenhang ist bemerkenswert, dass der damaszener Astronomen
Ibn al-Shatir (1304 - 1375) die Sonnenbahn nach [8], S.239 im geozentrischen System
durch die Funktion beschrieb. Das sehr große Verhältnis
zwischen größter und kleinster Entfernung der Sonne von der Erde (heutiger
Wert:1,034) sollte vermeintliche Größenunterschiede der Sonnenscheibe erklären.

In Anbetracht der Tatsache, dass Kopernikus durch den Wechsel zum heliozentrischen
Koordinatensystem die Bahnbeschreibung der äußeren Planeten von der Erdbewegung
abkoppeln konnte, ist es merkwürdig, dass er beim Bewegungsmodell für die Planeten
Venus und Merkur eine gleichförmige Kreisbewegung mit einer Umlaufzeit von genau
einem halben Jahr verwendete. Hierbei kommt indirekt der Term zum Tragen,
wobei bzw. die Exzentrizität bzw. die mittlere Winkelgeschwindigkeit der Erde
sind, und t die seit einem Periheldurchgang der Erde vergangene Zeit ist. Um dies
nachzuvollziehen, ist der Wechsel in ein geozentrisches Koordinatensystem sinnvoll. Wenn
die x-Achse hierbei parallel zur Apsidenlinie der Erdbahn gelegt wird und man die Näherung
durch die Funktion K benutzt, ergibt sich die Bewegungsfunktion
.
ist das Verhältnis der großen Halbachsen von Venus und Erde und die Differenz der
Perihellängen. ist die Zeit eines Periheldurchgangs der Venus. Die Exzentrizität e der
Venus mit dem modernen Messwert 0,0068 ist so klein, dass der Wert mit den
Beobachtungsmöglichkeiten von Kopernikus nicht von Null unterschieden werden konnte.
Die Funktion passt zu der von Kopernikus benutzten Bewegungsfunktion
. Sie ergibt sich, wenn man die
Daten in [3], V,23 , die dort mit dem Antifokus Z der Erdbahn als Zentrum dargestellt sind,
in ein geozentrisches System umrechnet. Der Wert 0,0246 entspricht (heutiger Wert:
0,0251), und 0,0104 entspricht . Die Funktion , die Kopernikus für die
Erdbahn nicht benutzt hat, ist also versteckt in der Beschreibung der Venusbahn enthalten.
Der Wert 0,719 für ([3], V,21) wird heute zu 0,723 gemessen. Zwar ist Kopernikus
mit dem Bewegungsmodell der Venus nicht wirklich eine Beschreibung im heliozentrischen
System gelungen, es eignete sich aber für Prognosen. Ähnlich gute Übereinstimmungen wie
bei der Venus findet man bei dem Planeten Merkur nicht, da er wegen der Nähe zur Sonne
besonders schlecht zu beobachten ist.

Kopernikus wie auch orientalische Astronomen vor ihm bezogen sich bei allen ihren
Untersuchungen auf die Theorie von Claudius Ptolemäus [10], die sehr gute Voraussagen
für die Planetenbahnen ermöglichte, aber dabei Kreisbahnen mit nicht konstanten
Winkelgeschwindigkeiten voraussetzte. Daran nahm man Anstoß, da dies dem schon von
Aristoteles formulierten Postulat der Rückführung aller Bewegungen auf einfachste
Grundformen widersprach. Auch Ptolemäus selbst hatte diesen Grundsatz akzeptiert
([10],III,3), missachtete ihn dann aber stillschweigend.

Ptolemäus beschrieb die Bewegung der äußeren Planeten Mars, Jupiter und Saturn im
geozentrischen System durch die Überlagerung von zwei
Bewegungen mit kreisförmigen Bahnen auf geringfügig gegeneinander geneigten Ebenen,
wobei der größere Kreis Deferent und der kleinere Epizykel genannt wurde. D ist der
konstante Mittelpunkt des Deferentkreises. Nur die Epizykelbewegung ist
dabei gleichförmig, und zwar wird davon ausgegangen, dass der Vektor stets
parallel ist zum Radiusvektor der kreisförmigen angenommenen Sonnenbahn mit einem
Mittelpunkt O, der nicht mit dem Erdmittelpunkt F übereinstimmt. Die Bewegung
erscheint nur dann als gleichförmig, wenn man sie von dem Punkt Ä
aus betrachtet, der durch Spiegelung vom Erdmittelpunkt F an D entsteht. Ä wird
Äquant oder Ausgleichpunkt genannt.

Dadurch dass Kopernikus den Ursprung des Koordinatensystems in den Antifokus Z der
Erdbahn verrückte, fiel der Term weg, so dass die Planetenbewegung nach
Ptolemäus durch die einfachere Funktion beschrieben werden konnte.
Diese Umdeutung des ptolemäischen Bewegungsmodells ist in Abbildung 2 für e = 0,85
dargestellt. Sie zeigt den Kreis um D, auf dem sich der Planet P mit der Umlaufzeit T
so bewegt, dass der Winkel M beim Ausgleichpunkt Ä zur Zeit t durch die mittlere Anomalie
gegeben ist. Der Radius des Kreises sei 1. Die Exzentrizität e ist hier die
Entfernung des Punktes D von Z und von Ä. Der exzentrischen Anomalie bei der Kepler-
Gleichung entspricht hier der Winkel E bei D. Der Winkel DPÄ wird durch
bestimmt. Wenn man den Sinussatz auf das Dreieck DPÄ anwendet, folgt ,
also . Legt man den Ursprung des Koordinatensystems in den
Punkt D und nimmt als Bahnradius die Längeneinheit, so ist die
Funktion der Ptolemäus-Bewegung. Diese beschreibt die Planetenbahn besser als die
Kopernikus-Bewegung. Von der Erde aus gesehen beträgt beim Mars die maximale
Abweichung zwischen der Kepler-Bewegung und der Ptolemäus-Bewegung 34
Bogenminuten, die zwischen der Kepler-Bewegung und der Kopernikus-Bewegung aber
50 Bogenminuten. Die Gleichung ergab eine so gute Näherung
für die exzentrische Anomalie, dass Kepler in [6] mit dieser von ihm so genannten
'stellvertretenden Hypothese' die Marsbahn berechnen und als Ellipse erkennen konnte.
Dabei setzte Kepler anders als Kopernikus die Sonne selbst auf die Apsidenlinie durch
Ä und D, allerdings nicht im gleichen Abstand von D wie Ä ([6], 16).

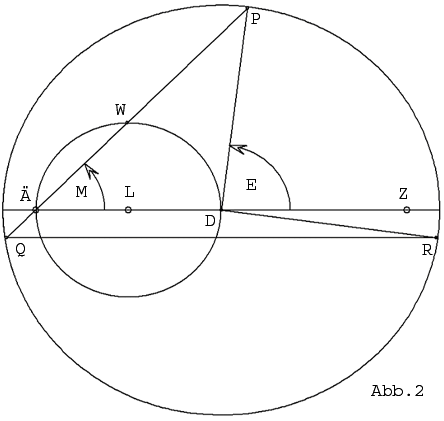
Aus Abbildung 2 wird klar, dass der Mittelwert der Bewegung nach dem Ptolemäus-Modell
durch den Mittelpunkt L des Kreises durch Ä und D mit dem Radius gegeben ist. Denn
der Mittelpunkt W zwischen P und dem Planetenort Q zur mittleren Anomalie M + p liegt
auf der Mittelsenkrechten von PQ und darum auf dem Kreis um L. Dieser Mittelpunkt W
bewegt sich bei gleichmäßig wachsendem Winkel M mit konstanter Geschwindigkeit auf dem
Kreis weiter, so dass der Mittelwert dieser Bewegung L ist. Folglich ist = - 0,5e der nullte
Fourier-Koeffizient der Ptolemäus-Bewegung.

Auch der Fourier-Koeffizient lässt sich aus der Abbildung 2 ablesen. Es sei R nämlich der
Schnittpunkt der Parallelen durch Q zu DZ. Dann gibt 2M den Winkel RDP an. Wenn P
seinen Kreis durchläuft, bewegt sich R spiegelbildlich zu Q. Da der Mittelwert von Q der
gleiche ist wie der von P, liegt der Mittelwert von R spiegelbildlich zu L. Darum ist = 0,5e
wie bei der Kepler-Bewegung.

Der historisch erste Weg zur Ersetzung der Ptolemäus-Bewegung durch eine Überlagerung
von gleichförmigen Kreisbewegungen setzte jedoch anders an. Nasir al-Din al-Tusi untersuchte,
wie sich der Punkt P auf der Geraden ÄP mit wachsender mittlerer Anomalie bewegt [5].
Er approximierte diese Bewegung durch eine Kosinus-Schwingung und beschrieb sie als
Überlagerung zweier Kreisbewegungen mit den Winkelgeschwindigkeiten w und - w, die
darum auch als Tusi-Paar bezeichnet wird. Wir folgen diesem Gedankengang im Beweis von

Satz 4: Für die Fourier-Koeffizienten der Ptolemäus-Bewegung mit geradzahligen k gilt:
, und = 0 sonst.
Für die Fourier-Koeffizienten mit ungeradzahligen mit gilt:
.
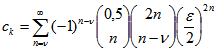Beweis:
Dass die Reihe zur Darstellung der Koeffizienten konvergiert, folgt wegen 0 < e < 1
aus dem Quotientenkriterium.
Die Länge der Strecke ÄP in Abbildung 2 ergibt sich auf Grund des rechtwinkligen Dreiecks
ÄWD zu (auch für M > 90°). Die Ptolemäus-Bewegung lässt sich
darum anders als oben auch durch beschreiben.
Nach Nasir al-Din al-Tusi wird durch ersetzt. Statt wie Tusi
durch 1 zu ersetzen, entwickeln wir die Wurzel in einer Binomialreihe:

Mit Hilfe von kann man auch als Überlagerung von
Kreisbewegungen darstellen:




.
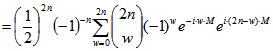
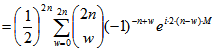
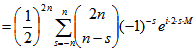
In dieser letzten Summe stimmen für die Koeffizienten von für s = n und s = - n
überein. Wenn man in der Summe 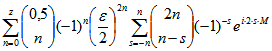die Summanden
mit der Potenz zu zusammenfasst und den Grenzübergang durchführt,
ergibt sich 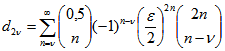. Der entsprechende Wert stimmt
damit überein. Für die Ptolemäus-Bewegung ergibt sich darum
. Daraus folgt die Behauptung von Satz 4.

Wenn man Potenzen von e mit Exponenten größer als 2 vernachlässigt, erhält man für die
Ptolemäus-Bewegung die Fourier-Koeffizienten
.
Ein Vergleich mit den entsprechenden Koeffizienten bei Kepler und bei Kopernikus macht
plausibel, dass die Approximation mit dem Ptolemäus-Modell etwas besser war als die
nach dem Kopernikus-Modell. Bemerkenswerterweise stimmen aber alle drei Modelle
in erster Näherung überein.

[1] Amann, H., Escher, J., Analysis II, Birkhäuser Verlag 2006
[2] Copernicus, Nicolas, Commentariolus in: Three Copernican Treatises, Octagon Books, New York 1971
[3] Copernicus, Nicolas, On the Revolutions, The John Hopkins University Press, Baltimore 1978
[4] Kaballo, W., Einführung in die Analysis II, Spektrum Akademischer Verlag 1997
[5] Kennedy, E.S., Late Medieval Planetary Theory, Isis, Vol. 57, No.3 , The University of Chicago Press 1966
[6] Kepler, Johannes, Neue Astronomie, R.Oldenbourg Verlag, München 1990
[7] Koestler, Arthur, The Sleepwalkers, Penguin Books, London 1959
[8] Saliba, George, Arabic Astronomy, New York University Press, New York 1994
[9] Stumpf, K., Himmelsmechanik, Bd.1, VEB Deutscher Verlag der Wissenschaften, Berlin 1973
[10] Toomer, G.J., Ptolemy`s Almagest, Princeton University Press, Princeton 1998