Es lebe die Geometrie!

Polygon-Billard und Spiegelungen

Auf dieser Seite werden Billard-Trajektorien in Polygonen im Zusammenhang mit Spiegelungen untersucht.

(Wir setzen im Folgenden das Abbildungs-Zeichen A rechts neben das Urbild-Zeichen u, damit bei
Hintereinanderschaltungen von Abbildungen die Abfolge der Abbildungen zur Leserichtung passt.)

Es seien A und B die Spiegelungen zu den Polygon-Seiten a und b. Bei Reflexion an a entsteht aus einer
Trajektorien-Strecke t die folgende Strecke u und daraus durch Reflexion an b die Strecke v. Bei der
Spiegelung von u an a ergibt sich die Strecke uA, die t geradlinig fortsetzt. Entsprechend setzt vB die
Strecke u geradlinig fort. Folglich ist vBA eine geradlinige Fortsetzung von uA. Bei dieser 'Linearisierung'
der Trajektorie ist also die Abfolge BA der Spiegelungen gegenüber der Abfolge a b der Seiten, an denen
reflektiert wird, vertauscht. Dies gilt auch bei mehr als zwei Reflexionen. Wenn also v an c in die folgende
Strecke w reflektiert wird, setzt wCBA die Strecke vBA geradlinig fort. Einer endlichen Trajektorie wird
so eine endliche Folge von Spiegelungen an Polygon-Seitengeraden zugeordnet, die wir 'Linearisierungs-
Folge' nennen. Sie beschreibt den 'Typ' einer Trajektorie. Die Abbildung, die durch Hintereinanderschaltung
in umgekehrter Reihenfolge daraus entsteht, nennen wir 'Linearisierungs-Abbildung'. Wenn diese Abbildung
als Hintereinanderschaltung von Spiegelungen dargestellt wird, ergibt sich daraus durch Lesen von rechts
nach links die Linearisierungs-Folge und damit der Typ. Die Linearisierungsabbildung bildet die letzte Strecke
der Trajektorie orientierungstreu in die letzte Strecke der Linearisierung ab, also auch den Endpunkt Z der
Trajektorie in den Endpunkt Z' der Linearisierungs-Strecke.

Bei einer unendlichen Trajektorie, die periodisch ist, geben wir den Typ durch die Linearisierungs-Folge einer
Periode an. Dabei beschreibt eine Folge, die durch eine zyklische Permutation entsteht, den gleichen Typ. Im
Fall einer geradzahligen Folgenlänge ist die zugehörige Linearisierungs-Abbildung stets eine Translation, die
den Startpunkt S = Z der Trajektorie in Z' abbildet und deren Verschiebungs-Vektor die Richtung der ersten
Trajektorien-Strecke angibt. Im Fall einer ungeraden Anzahl wie beim Typ CBA in der folgenden Gleitschau
ist die Linearisierungs-Abbildung eine Gleitspiegelung . S und die erste Strecke müssen dann auf der
Gleitspiegelungs-Achse liegen, damit sich eine ungerade Periode ergibt. Wenn S dabei kein Eckpunkt ist,
führen stets benachbarte Startpunkte zu einer Periode mit doppelter Strecken-Anzahl, bei der jede Strecke
der ungeraden Periode in zwei dazu parallele Strecken aufgespalten ist. Die zugehörige Linearisierungs-
Abbildung ist dann die Translation .

Im Folgenden wird gezeigt, wie man aus der Angabe der Linearisierungs-Abbildung einer periodischen
Trajektorie leicht den Richtungswinkel der ersten Strecke berechnen kann. Eine Linearisierungs-Abbildung
der Form hat darüber hinaus den Vorteil, dass mit dem Schnittpunkt S der Achse von und der
Dreiecks-Seite c auch ein Startpunkt leicht bestimmt werden kann. Dieser definiert zudem die Mitte des
Start-Intervalls, das zu der Linearisierungs-Abbildung gehört. Eine Gleitspiegelung , die sich durch eine
Hintereinanderschaltung von Spiegelungen an Seiten des Dreiecks ergibt, kann nur dann Linearisierungs-
Abbildung einer periodischen Trajektorie sein, wenn ihre Achse die Seite c schneidet.


Bei periodischen Trajektorien setzen wir den Startpunkt S stets auf den Rand des Polygons.

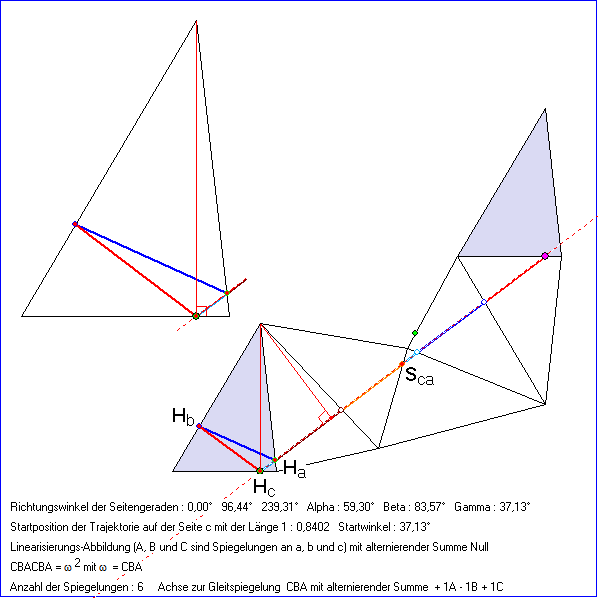
Die Gleitschau zeigt Billard-Trajektorien in einem unregelmäßigen Dreieck mit den Startwinkel 37,13°
und 74,26° bei einem Start auf der Seite c des Billard-Dreiecks. 37,13° ist die Größe des Innenwinkels
an der oberen Ecke des Dreiecks und die des Winkels, den die Seite c mit der Geraden g durch die
Höhen-Fußpunkte und einschließt.

Die Trajektorie wird im Fall von 37,13° nacheinander an den Seiten a, b, c, a, b und c reflektiert, so dass
die Linearisierungs-Abbildung die Translation CBACBA ist. Die Linearisierungs-Strecke durchläuft dann
nacheinander die Bilder des Billard-Dreiecks bei den Abbildungen A, BA, CBA, ACBA und BACBA, und
sie endet in dem Punkt Z', der das Bild des Zielpunkts Z bei der Verschiebung CBACBA ist. Für Startpunkte
in der hier betrachteten Umgebung vom Höhenfußpunkt auf c ist die Trajektorie darum periodisch.
Wenn S gleich ist, folgt die Trajektorie im Fall von 37,13° dem Höhen-Fußpunkt-Dreieck, so
dass die kleinste Periode nur aus drei Strecken besteht. Die zugehörige Linearisierung-Abbildung CBA
ist eine Gleitspiegelung. Der Eckpunkt des Dreiecks gegenüber a wird durch CBA in den gleichen
Punkt abgebildet wie bei Spiegelung an a, und der Punkt, der aus dem oberen Eckpunkt durch
Spiegelung an c entsteht, wird durch CBA in den Eckpunkt zurück abgebildet. Darum ist g die Achse
von CBA, denn der Mittelpunkt zu jedem Urbild-Bild-Paar liegt auf der Achse. Diese Gleitspiegelung
bildet in den Punkt ab, dessen Abstand von mit der Länge vom Umfang des Höhenfußpunkt-
Dreiecks übereinstimmt und der sich auch bei Spiegelung von am Lot vom oberen Eckpunkt auf g
ergibt. Wenn S nicht der Höhenlotfuß ist, besteht die Periode aus sechs Strecken parallel zu den Seiten des
Höhenfußpunkt-Dreiecks. Die Trajektorien-Eckpunkte liegen auf jeder Seite des Dreiecks symmetrisch
zu den Höhenfußpunkten. Deshalb ist der Typ CBACBA nur bei einem Startpunkt S in dem zum Fußpunkt
der Höhe symmetrischen Intervall möglich, auf dessen Rand einer der beiden Endpunkte von c liegt. Dieser
Typ kann bei einem stumpfwinkligen Dreieck nicht vorkommen, da dann nicht alle Höhenfußpunkte auf
dem Rand des Dreiecks liegen.

Im Fall von 74,26° ist die Linearisierungs-Abbildung die Translation CBABACBABA, falls der Startpunkt
auch hier in dem Intervall mit dem Mittelpunkt und einem Eckpunkt als Randpunkt liegt. Für S gleich
ist die Trajektorie periodisch mit fünf Strecken, sonst mit zehn. Die Achse der Gleitspiegelung CBABA geht
durch .

Bei einem kleinerer Innenwinkel Gamma an der Spitze des Billard-Dreiecks kann es auch eine periodische
Trajektorie mit der Linearisierungs-Abbildung CBABABACBABABA geben. Allgemein gilt:
In einem spitzwinkligen Dreieck ergibt sich für die Linearisierungs-Abbildung mit bei
den gleichen Startpunkten wie für CBA eine Periode, falls das n-fache von Gamma kleiner als 90° ist.



In der Gleitschau wird der Begriff 'alternierende Summe' benutzt, der für die Analyse von Spiegelungs=
produkten nützlich ist. Dieser Begriff soll im Folgenden erklärt werden.

Der Richtungswinkel einer orientierten Strecke oder Geraden g sei mit r(g) bezeichnet. Wenn g nicht
orientiert ist, benutzen wir die gleiche Bezeichnung, identifizieren dann aber Winkelgrößen, die sich
um 180° unterscheiden. Das ist sinnvoll bei Geraden oder Polygon-Seiten, an denen gespiegelt wird.
Wenn die Trajektorien-Strecke t an einer Seite a reflektiert wird, ist der Richtungswinkel der folgenden
Strecke u durch gegeben. Bei einer Fortsetzung durch Reflexionen
an den Seiten b und c, ergeben sich nacheinander die Richtungswinkel und
. Die Richtungswinkel der Seiten gehen also in eine alternierende Summe
ein, bei der die Vorzeichen '+' und '-' abwechselnd vorkommen, und das Vorzeichen von r(t) ist '+'
oder '-', je nachdem, ob die Anzahl der Reflexionen gerade oder ungerade war.

Ein ähnliche Muster finden wir bei der Linearisierungs-Abbildung. Als Richtungswinkel der Spiegelung
A an a definieren wir r(A) := r(a). Die Hintereinanderschaltung BA zweier Spiegelungen ist eine Drehung
mit dem halben Drehwinkel oder im Fall eine Translation (Verschiebung) .
Aus BA = DC folgt . Darum kann die Funktion r für Zweier-Produkte durch
definiert werden. Die Hintereinanderschaltung CBA dreier Spiegelungen ist eine
Gleitspiegelung oder Spiegelung, bei der die Achse den Richtungswinkel hat. Darum
ist für das Dreierprodukt die Definition möglich. Für die inverse Abbildung
stimmt der Richtungswinkel damit überein. Beim Produkt DCBA von vier Spiegelungen ist der halbe Drehwinkel einer Drehung oder Null im Fall einer
Translation. Für EDCBA ergibt sich wieder eine Gleitspiegelung oder Spiegelung, deren Achse den
Richtungswinkel hat. Für längere Produkte setzt sich
dieses Prinzip analog fort.

Wir definieren für eine Folge , , , ... von Spiegelungen, die möglicherweise nicht verschieden sind,
in folgender Weise eine 'alternierende Summe': Wir zählen ab, wie oft jede vorkommende Spiegelung mit
geradzahligem bzw. ungeradzahligem Index vorkommt, und ziehen die zweite Anzahl von der ersten ab.
Das Ergebnis wird die Vorzahl dieser Spiegelung in einer formalen Summe mit den Zeichen für die
vorkommenden Spiegelungen als Variablen-Namen. Im Beispiel des Typs BACBABABA indizieren wir
von rechts nach links und erhalten die alternierende Summe . Es gibt nämlich A dreimal an
gerader Stelle und einmal an ungerader, B einmal an gerader und dreimal an ungerader Stelle und C einmal
an gerader Stelle. Der Sinn dieser Definition folgt daraus, dass der Richtungswinkel
der Achse der Gleitspiegelung BACBABABA ist. Ein entsprechender Zusammenhang gilt für alle Produkte
von Spiegelungen. Die alternierende Summe ist auch bei der Entscheidung nützlich, ob ein Produkt von
Spiegelungen eine Translation ist. Dies ist nämlich genau dann der Fall, wenn die Anzahl der Spieglungen
gerade ist und der r-Wert zur alternierenden Summe Null. Das gilt insbesondere dann, wenn die alternierende
Summe selbst gleich Null ist, d. h. wenn alle Vorzahlen Null sind.

Wenn BACBABABA die Linearisierungs-Abbildung einer Trajektorie ist, die mit der ersten Strecke t startet,
dann ist der Richtungswinkel der letzten, also zehnten Strecke. Bei Verkürzung
der Trajektorie um eine Strecke ergibt sich als Richtungswinkel der letzten,
also jetzt neunten Strecke. Bei einer Spiegelungsanzahl n und einer Linearisierungs-Abbildung erhält man
den Term für den Richtungswinkel der letzten Strecke.

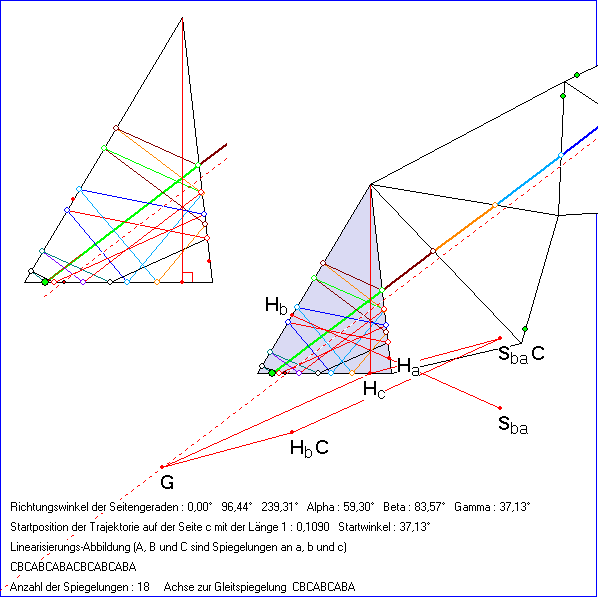
In der vorherigen Gleitschau wurde gezeigt, dass es bei dem dort betrachteten spitzwinkligem Dreieck
eine periodische Trajektorie vom Typ CBACBA gibt, wenn der Abstand des Startpunkt S auf der Seite
c vom rechten Eckpunkt kleiner ist als das Doppelte des Abstand des Höhenfußpunkts. Dabei war der
Startwinkel so groß ist wie der Innenwinkel im Eckpunkt, der c gegenüber liegt. Die Startstrecke ist dann
parallel zur Achse der Gleitspiegelung CBA durch die Höhenfußpunkte auf c und a. In dieser Gleitschau
werden die Trajektorien bei gleichem Startwinkel für andere Startpunkte untersucht.

Im Intervall [0 ; 0,4194] (0 beim linken Eckpunkt, 1 beim rechten) ergibt sich eine Trajektorie vom Typ
mit . Dabei ist eine Gleitspiegelung, deren
Achse wegen die gleiche Richtung wie CBA hat. Der Schnittpunkt der
Achse von liegt in der Mitte des Intervalls zwischen 0 und 0,4194 (gerundet). Wenn der Richtungswinkel
bekannt ist, reicht ein Punkt zur Bestimmung der Achse. Dies kann der Mittelpunkt eines beliebigen Urbild-
Bild-Paares der Gleitspiegelung sein. Einen tieferen geometrischen Zusammenhang stellt folgende Überlegung
her, die zeigen soll, dass der Punkt G in der ersten Zeichnung der Gleitschau auf der Achse von liegt:
Zunächst errechnet man . Hierbei ist BCA eine Gleitspiegelung mit der Achse h durch
und , die in den Punkt auf h abbildet, dessen Abstand von mit der Umfangslänge u des
Höhenfußpunkt-Dreiecks übereinstimmt. (Für CBA wurde oben eine analoge Aussage hergeleitet.)
ist darum eine Translation parallel zu h mit der Verschiebungslänge u.. ist dann eine
Translation parallel zum Spiegelbild von h bei C mit der gleichen Verschiebungslänge. G sei der vierte
Parallelogramm-Punkt zu und den Spiegelungsbildern und .Der Punkt J, der durch Spiegelung
von an G entsteht, wird dann durch in abgebildet, so dass gilt, da bei BCA
fest bleibt. Darum liegt G auf der Achse von .

Für S im Intervall [0,4195 ; 0,6083] ergibt sich eine periodische Trajektorie mit der Periodenlänge 54 vom Typ
mit und . Da die Linearisierungs-
Abbildung auch hier quadratisch ist, reduziert sich die Periodenlänge zu 27, wenn S in der Mitte des Intervalls
auf der Achse von liegt. Im Intervall [0,6084 ; 0,6806] ist die Periodizität unklar. Jedenfalls gibt es hier
anscheinend keine Perioden mit einer Länge kleiner als 1000.

Die in der Gleitschau gezeigten Typen periodischer Trajektorien können in anders geformten Dreiecken nur
dann vorkommen, wenn die Gleitspiegelungsachsen die Seite c schneiden. Das ist bei CBACBA für alle
spitzwinkligen Dreiecke der Fall, nicht aber bei den anderen hier betrachteten Typen.

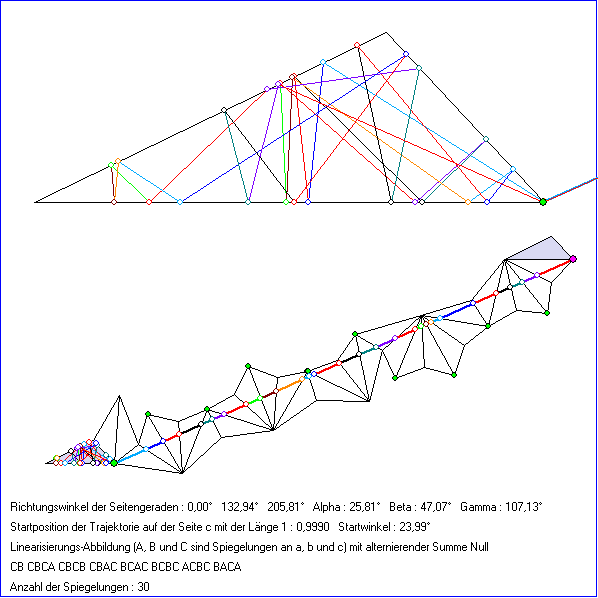
Die Gleitschau zeigt periodische Trajektorien bei einem stumpfwinkligen Dreieck Hier ist die Linearisierungs-
Abbildung jedoch nicht das Quadrat einer Gleitspiegelung. Die Trajektorien entstehen hier darum auch nicht
aus einer Aufspaltung einer Trajektorie mit halber Streckenzahl.

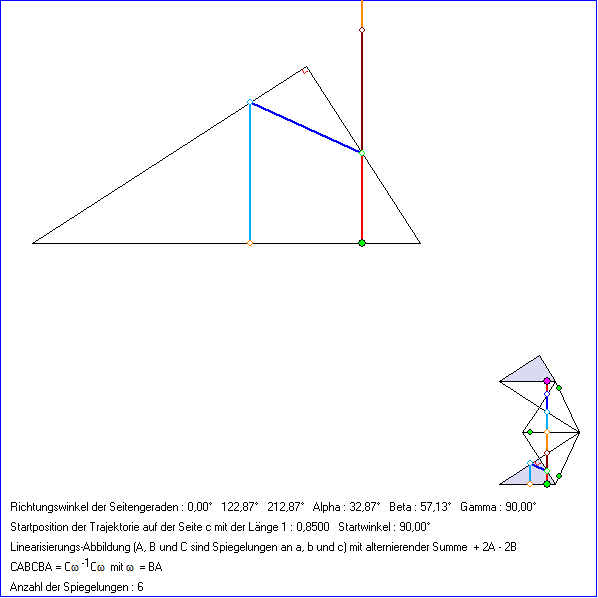
Die Gleitschau zeigt periodische Trajektorien in einem rechtwinkligen Dreieck, die nach einer halben
Periode den gleichenWeg zurück laufen. Das ist nur möglich, wenn zwei Trajektorien-Strecken senkrecht
auf Dreieck.Seiten auftreffen. Wenn dies beim Start und nach einer halben Periode die Seite c ist, hat die
Linearisierungs-Abbildung die Form . Im einfachsten Fall ist hierbei die Punktspiegelung AB
an dem Eckpunkt O mit dem rechten Winkel. In Sonderfällen kommt es vor, dass eine Trajektorie den
Punkt O trifft und daran zurück reflektiert wird. Dann gibt es ein Produkt von Spiegelungen an Dreiecks-
Seiten mit . In diesem Fall liegt der Startpunkt S in der Mitte eines Intervalls mit Startpunkten
von Trajektorien gleichen Typs, die sich durch Aufspaltung ergeben.

Bei großen Anzahlen von Spiegelungen wurde in der Gleitschau die Linearisierungs-Strecke zum Teil halbiert.
Die Trajektorie mit der Länge 1000 ist nicht periodisch.