Es lebe die Geometrie!

Unter einem regelmäßigen Vieleck zur Eckenzahl n und zur Überschlagungszahl m () verstehen wir ein n-Eck mit , das folgender Eigenschaft hat: Es gibt eine Drehung D zum Drehwinkel mit für alle i von 0 bis n-1. Die Eckpunkte liegen dann alle auf einem Kreis mit dem Radius R. Beim Quadrat ist n = 4 und m = 1, beim Pentagramm n = 5 und m = 2.

, sei die Kurve, die entsteht, wenn der Punkt P mit konstanter Bahngeschwindigkeit den Polygonzug in der Zeit T durchläuft. Die Fourier-Analyse dieser Bewegung ergibt eine Überlagerung , von gleichförmigen Kreisbewegungen mit dem Radius und der Winkelgeschwindigkeit für i zwischen und z. Wenn z gegen Unendlich geht, konvergiert gleichmäßig gegen . Dabei ist falls ist und i nicht in der Form dargestellt werden kann mit einer ganzen Zahl j. Wenn i in der Form dargestellt werden kann, gilt die Formel .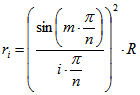

--> Pdf-Dokument zur Fourier-Analyse der Dreiecke
--> Pdf-Dokument zur Fourier-Analyse beliebiger Vielecke