Es lebe die Geometrie!

Heptagramma mirificum

Das Heptagramma mirificum, das seltsame Heptagramm, ist ein überschlagendes Großkreisbogen-Siebeneck
bei dem die aufeinander folgenden Seitenbögen rechtwinklich zusammentreffen. Wie das Pentagramma
mirificum gibt es auch hier eine Vielzahl von unregelmäßigen Modifikationen. Sie lassen sich mit einer
Variation der Napier-Konstruktion des Pentagramms aus einem Großkreisbogen-Viereck konstruieren.
Für die Abbildung , die von einem Viereck zum nächsten führt, ist dabei die identische Abbildung,
so dass sich die Vierecke zu einem Kranz an den Spitzen des Heptagramms zusammenschließen.

Die Animation zeigt die erweiterte Napier-Konstruktion für ein Ausgangs-Viereck, das zu einem
regelmäßigen Heptagramm führt. Drei Eckpunkte sind dabei aufeinander folgende Punkte des
regelmäßigen Siebenecks mit
. Der vierte Punkt
entsteht aus dem mittleren der drei Punkte durch Streckung aus dem Ursprung mit dem Faktor
.

Die Eckpunkte des Ausgangs-Vierecks der Napier-Konstruktion seien mit A, B , C und D gegen den
Uhrzeigersinn durchbuchstabiert, endend mit D beim rechten Winkel. Dann wird die Napier-Konstruktion
zunächst auf das Dreieck DAB angewandt. Die Seite AB wird also über B hinaus zu B ' verlängert, so dass
BB ' vom Pol der Seite AB aus unter dem Winkel 90° erscheint. Der Pol bildet dann also zusammen mit B
und B ' ein Polardreieck mit lauter rechten Winkeln und im Kugel-Modell lauter Seiten der Länge .
Entsprechend wird die Seite DA über A hinaus zu D ' verlängert.. Zur Konstruktion des vierten Eckpunktes
C ' des neuen Viereck ist eine Modifikation des Napier-Verfahrens nötig. Dazu wir das Polardreieck
um B gegen den Uhrzeigersinn so weit gedreht, bis eine Seite davon auf die Seite BC trifft. Der gegenüber
liegende Eckpunkt ist dann C '. Dies ist also der Pol des Großkreises durch B und C.

Die Gleitschau im Anschluss an die Animation zeigt Standbilder daraus.

Die Animation mit einem unregelmäßigen Heptagramma mirificum soll den Zusammenhang zwischen den
Winkeln und Seiten eines Vierecks und seines Bildes bei der erweiterten Napier-Konstruktion
zeigen. Dazu seien die Winkelgrößen zu einem 7-Tupel vereinigt in folgender Reihenfolge:
Länge r der roten Seite
Innen-Winkel s beim Eckpunkt zwischen roter und grüner Seite
Länge t der grünen Seite
Innen-Winkel u beim Eckpunkt zwischen grüner und blauer Seite
Länge v der blauen Seite
Innen-Winkel w beim Eckpunkt zwischen blauer und violetter Seite
Länge x der violetten Seite.
Die Daten des Ausgangs-Vierecks sind dann näherungsweise (63° ; 32° ; 43° ; 217° ; 34° ; 44° ; 49°)

Dann kommt man vom Tupel zu zu dem von durch die Abbildung


Es seien a, b, c und d die Seiten-Großkreise zu CA, DA, AB und BC. Mit der Pol-Polaren-Abbildung *
und der Antipoden-Abbildung kann folgendermaßen beschrieben werden: .
Man errechnet daraus, dass die identische Abbildung ist.

Die Animation zeigt Heptagramma, die symmetrisch zur Rechts-Achse sind.

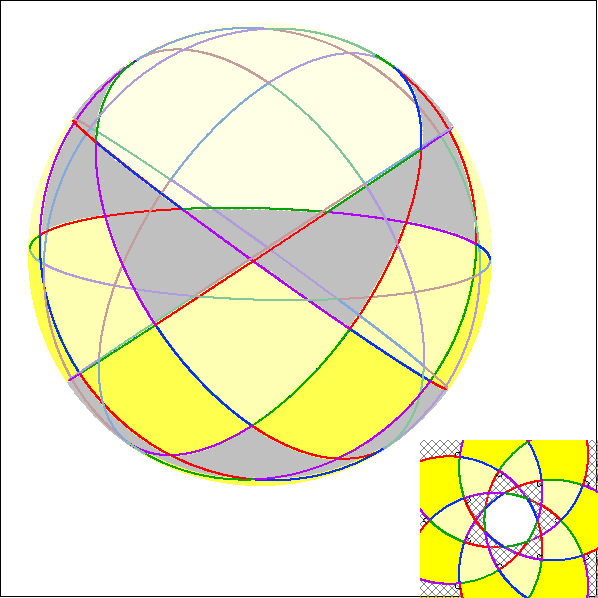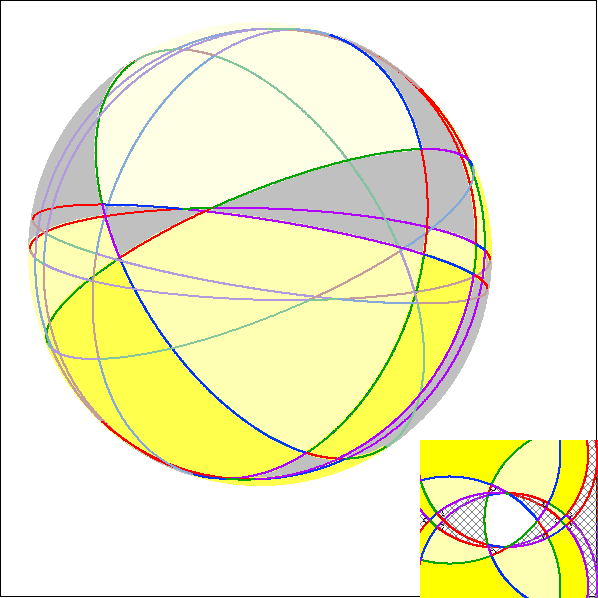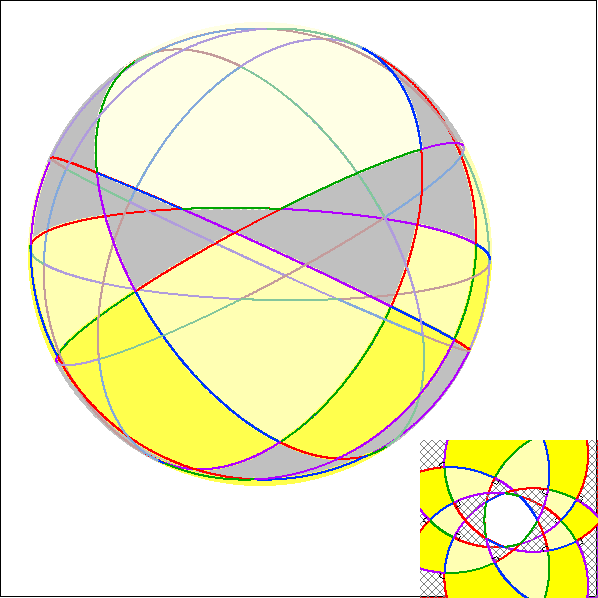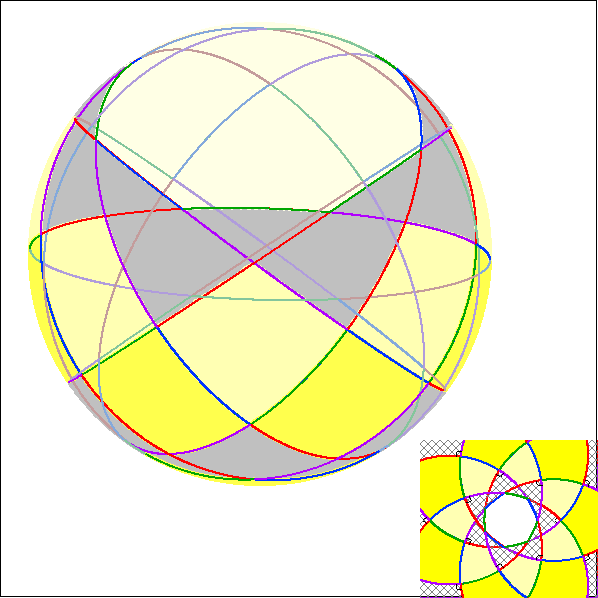
Hier werden zu den Heptagramma der vorherigen Animation die Seiten-Großkreise der zugehörigen
Darstellung im Kugel-Modell gezeigt.