Es lebe die Geometrie!

Clifford-Parallelismus

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum I'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum II'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_II.pdf

Auf der vorhergehenden Seite ' Schraubungen' wurde die Clifford-Translation zur Erzeugung der Regulus-
Geraden eines einschaligen Hyperboloids benutzt. Wir nennen die roten Geraden des einen Regulusses
Clifford-links-parallel (kurz: CL-parallel) und die des blauen Regulusses CR-parallel. Ein Bewegung,
welche jede Gerade in eine dazu links- bzw. rechts-parallele Gerade abbildet, bezeichnen wir als
CR- bzw. CL-Translation (oder -Schiebung). Auf der vorhergehenden Seite wurde eine Gerade g mit
einer CR- und einer CL-Translation bis zum Schnitt mit einem Kreis verschoben, der sich als Spur eines
Punktes P bei Drehung um g ergab. Jede Gerade auf dem Hyperboloid war also entweder CL- oder
CR-parallel zu g. Auf dieser Seite wird ein anderes Verfahren zur Erzeugung einer Regelfläche (Hyperboloid
oder hyperbolisches Paraboloid) dargestellt, das auch dann verwendbar ist, wenn es zu den roten Geraden h
und den blauen Geraden j keine Gerade g gibt, die zu h CL-parallel und zu j CR-parallel ist.

Wir beziehen uns dabei auf einen dreidimensionalen elliptischen Raum, in dem die Maßbestimmung für
Ebenen durch die symmetrische Bilinearform gegeben ist,
für Punkte durch und für Geraden durch
und . Dabei ist k eine positive reelle
Konstante und z.B. . In den folgenden Animationen ist k gleich 1.

A, B , C und D seien Punkte des Raumes, so dass AB und CD CL-parallel sind und AD und BC
CR-parallel. Dann nennen wir ABCD CL-Parallelogramm und ADCB CR-Parallelogramm. Wenn die
Eckpunkte A, B und D durch ihre Punkt-Quadrupel a, b und d gegeben sind, kann man das Quadrupel
c des vierten Eckpunktes C im CL-Parallelogramm folgendermaßen berechnen: Das Kreuz-Produkt
ist das Quadrupel w mit der Eigenschaft, dass für jedes Quadrupel v gilt .
Wenn die Determinante der Matrix ist, die sich ergibt, wenn man in der Matrix aus den drei Zeilen a, b
und d die i-te Spalte löscht, dann ist . Die zugehörige Ebene inzidiert mit A, B
und D. ist der Pol dieser Ebene. Dann ist c proportional zu
. Der vierte Eckpunkt C' im CR-Parallelogramm
ABC'D ergibt sich, indem man durch ersetzt. Wenn A, B und D kollinear sind, ist C der vierte
Spiegelungs-Punkt. Das bedeutet, dass die Hintereinanderschaltumg der elliptischen Spiegelungen an B, A
und D die Spiegelung an C ergibt. Für A ist dies die Abbildung für ein Quadrupel
p eines Raum-Punktes P, vorausgesetzt, dass a e-normiert ist.

Eine andere Möglichkeit der Darstellung von c erhält man mit dem Quaternionen-Produkt für Punkt-
Quadrupel p und q, das folgendermaßen definiert werden kann : Sei bzw. (red für 'reduziert') das
Tripel aus den ersten drei Komponenten von p bzw. q und das innere Produkt davon. Dann ist
und . Die Verknüpfung * ist assoziativ,
aber nicht kommutativ, da sich bei Vertauschung der Faktoren beim Kreuz-Produkt das Vorzeichen ändert.
Mit dem zu a konjugierten Quadrupel ist Quadrupel von C für ein
CL-Parallelogramm ABCD. Wenn ABCD CR-Parallelogramm ist, muss man b und d vertauschen.

In jedem CL-Parallelogramm oder CR-Parallelogramm ABCD haben AB und DC , sowie AD und BC
den gleichen elliptischen Abstand. Dies entspricht also den Bedingungen bei Parallelogrammen in der
euklidischen Geometrie, die aber im Gegensatz zu Clifford-Parallelogrammen stets komplanare Eckpunkte
haben. Die elliptische Größe des Winkels zwischen den Ebenen ABC und BCD stimmt mit der zwischen
den Ebenen CDA und DAB überein und hat den gleichen Wert wie die Abstände von AD und BC . Der
gleiche Zusammenhang zeigt sich, wenn man die Punkt-Bezeichnungen um eine Position zyklisch
weiterrückt.

Diese Animation geht von einem CL-Parallelogramm ABCD mit gleich langen Seiten der Länge 40°
aus. Durch Teilung gegenüberliegender Seiten im gleichen elliptischen Teilverhältnis werden Regulus-
Geraden zu einem hyperbolischen Paraboloid erzeugt. Die euklidische Teilverhältnis-Konstante tvk
ist hier gleich 1. Realisiert wird die Erzeugung der Regulus-Geraden durch CL-Translationen längs
AB und CR-Translationen längs AD, die auf die Geraden AD bzw. AB angewandt werden. Die roten
Geraden des L-Regulusses und die blauen Geraden des R-Regulusses, welche die Seiten AD bzw. AB
im gleichen elliptischen Teilverhältnis teilen, schneiden sich in der magentafarbenen Parabel. Die hellgrüne
Parabel entsteht dadurch, dass bei den roten L-Regulus-Geraden die innere Teilung durch die äußere
Teilung der Strecke zwischen den Schnittpunkte mit den Seiten-Geraden BC und AD ersetzt wird. Nach
einer 360°-Drehung des Paraboloid wird im letzten Teil der Animation der Winkel BAD vergrößert mit
dem Effekt, dass aus dem Paraboloid ein einschaliges Hyperboloid, aus der roten Parabel eine Ellipse
und aus der grünen eine Hyperbel entsteht.

Wenn das CL-Parallelogramm ABCD durch Quadrupeln a, b, d und gegeben ist, gibt es
durch jeden Punkt R der zugehörigen Regelfläche (Hyperboloid oder hyperbolisches Paraboloid) eine
Links-Parallele g zu AB und eine Recht-Parallele h zu AD. g schneidet AD in einem Punkt Q und h trifft
AB im Punkt P. Es gibt reelle Zahlen s, s', t und t' mit und . Wenn P und Q
nicht gerade unendlich ferne Punkte sind, kann man für s' und t' auch 1-s bzw. 1-t setzen, um so ein
Koordinaten-Paar (s ; t) zu dem Punkt R zu erhalten. Da R vierter L-Parallelogramm-Punkt zu APRQ ist,
ist Quadrupel von R. Da mit jedem Quaternion vetauschbar
ist, errechnet man

.
Diese Darstellung zeigt, dass
eine Gleichung für die Regelfläche ist, denn sie wird bei Einsetzung von r an Stelle von x erfüllt. Die
euklidische Teilverhältnis-Konstante tvk, die auf der Seite ' Hyperboloid 2' erklärt wird, ist nicht der
Kehrwert von fp(a;a), weil insbesondere c nicht als vierte Komponente 1 hat. Wenn man a, b, c und d
so normiert, dass sie die vierte Komponente 1 haben, muss der Faktor in der Gleichung der
Regelfläche geändert werden, nämlich in die euklidische Teilverhältnis-Konstante
.

Das erste Bild dieser Animation zeigt eine gelbe Figur mit Seiten auf drei L-parallelen Geraden a1 =AB,
a2, a3 = CD und drei R-parallelen Geraden b1 = AD , b2, b3 = BC . Sie wurde von Germinal Dandelin
(1794-1847) als 'Hexagramme mystique' bezeichnet. Neben den sieben markierten Punkten der gelben
Figur gibt es zwischen diesen sechs Geraden nur noch die Schnittpunkte B und D. Die drei Schnittpunkte
Si der Geraden ai und bi für i = 1, 2, 3 bilden das grün markierte Dreieck. Die in diesem Dreieck dem
Punkt Si gegenüberliegende Gerade sei ci genannt. Die fett schwarz gezeichneten Geraden a4 und b4 des
ersten Bilds gehören zum L- bzw. R-Regulus der zur gelben Figur gehörigen Regelfläche. a4 und b4 schneiden
sich darum und liegen in der Ebene D, die man als Tangential-Ebene der Regelfläche ansehen kann.

Die drei rot berandeten Geraden ai (i = 1, 2, 3) schneiden D in Punkten Pi von b4 und die blau berandeten
Geraden bi (i = 1, 2, 3) schneiden D in Punkten Qi von a4. Die drei Geraden ci (i = 1, 2, 3) treffen D in den
Punkten Ri. R1 liegt auf den dünn schwarz gezeichneten Geraden P2Q3, da c2, a2 und b3 gemeinsam in
einer Ebene liegen. Denn c1 trifft a2 in S2 und b3 in S3 und a2 und b3 sich schneiden sich, weil sie zu
verschiedenen Regulussen gehören. Analog erkennt man auch, dass R1 auf P3Q2 liegt. Die Punkte Pi, Qj
und Rk sind genau dann kollinear, wenn i, j und k drei verschiedene Zahlen sind.

Die Ebene E des grünen Dreiecks S1S2S3 schneidet D in der grünen Geraden durch R1, R2 und R3, so
dass zusammen mit den sechs Punkten P1, P2, P3, Q1, Q2, Q3 die Figur des Satzes von Pappos (um 300)
entsteht. Dieser Satz ist hier eine Folge davon, dass jede der Geraden a1, a2, a3 jede der Geraden b1, b2, b3
schneidet

In der Animation wird die Konfiguration des 'Hexagramme mystique' um 360° gedreht und anschließend
die Regelfläche hinzugefügt. Sie hat die eukidische Teilverhältnis-Konstante tvk = 1,0086 nahe bei 1, ist
also ein Hyperboloid, das lokal einem hyperbolischen Paraboloid ähnelt. Die Ebene E wird parallel
verschoben. Dabei ändert sich die fett gezeichnete schwarz-graue Schnittkurve mit dem Hyperboloid
von einem Geraden-Paar in eine Hyperbel und die Figur des Satzes von Pappus in die des Satzes von
Pascal (1623-1662).

Wenn man ausgehend vom CL-Parallelogramm ABCD die Punkte P bzw. Q von A bzw. B in
Richtung D bzw. C R-parallel verschiebt und dabei die elliptischen Abstände P von A und Q von
B stets den gleichen Wert haben, dann wird die Gerade PQ R-parallel verschoben und man
kommt beim Wert 180° wieder bei den Ausgangspunkten A bzw. B an. Die Gerade PQ trifft
unterwegs jeden Punkt der zu ABCD gehörigen Regelfläche. Beim Wert 90° erreicht sie die
L-Regulus-Gerade, die in der Regelfläche genau gegenüber AB liegt. Wir nennen sie 'Antipoden-
Gerade zu AB'. Es gibt zwei zueinander polare Geraden m und m' mit der Eigenschaft, dass die
gemeinsame Spiegelung an m und m' jede Gerade auf der Regelfläche in ihre Antipoden-Gerade
abbildet. Die Konstruktion von m und m' soll in der Animation gezeigt werden.

In der ersten Hälfte der Animation wird die Konstruktion für Punkte P und P' auf AD im Abstand 90°,
sowie Q und Q' auf BC im Abstand 90° dargestellt. Die roten Geraden g = PP' und h = QQ' sind
L-parallel. Durch jeden Punkt von g und auch von h gibt es eine Gerade j, die elliptisch orthogonal
zu beiden Geraden g und h ist. Ein derartiges gemeinsames Lot j ist magentafarbig eingezeichnet. Die
erste Bewegung (hin und her) zeigt verschiedene Möglichkeiten für j bei festgehaltener Geraden g. Bei
der zweiten Bewegung wird g R-parallel verschoben. Die Lotfußpunkte L und L' haben dabei stets den
Abstand 83,58°. Auf j sind zu den magentafarbigen Lotfußpunkten die beiden elliptischen Mittelpunkte
M und M' eingezeichnet. M hat von L und L' den elliptischen Abstand 83,58°/2, M' den Abstand
(180°-83,58)/2. M und M' bewegen sich bei jeder der beiden Hin-und-Her-Bewegungen auf den
grauen Geraden m und m', die ebenfalls elliptisch orthogonal zu j sind. Die gleichen Geraden m und m'
ergeben sich, wenn man P und Q auf AB und CD bewegt.

Wenn (u ; v) normiertes Tripel-Paar der Geraden AD ist, kann man folgendermaßen die
CR-Translation längs AD zum Abstand für ein beliebiges Punkt-Quadrupel
mit der oben angegebenen Quaternionen-Multiplikation beschreiben :

Bei einer CL-Translation hat man die entsprechende Abbildungs-Vorschrift mit einem
geänderten Vorzeichen vor der Wurzel und vertauschter Reihenfolge der Quaternionen:

Wenn der Verschiebungs-Abstand 90° beträgt, wird x mit einem Quaternion multipliziert,
dessen vierte Komponente Null ist und bei dem die ersten drei Zahlen einen Vektor der
euklidischen Länge 1 ergeben, falls (u ; v) normiert ist.

Eine andere Möglichkeit zur Clifford-Translation der Punkte bietet die auf der vorhergehenden
Seite 'Schraubungen' definierte Abbildung mit für die CL-Translation
und für die CR-Translation. Bemerkenswerterweise kann stattdessen auch eine Schraubung
zum Tripel-Paar

mit + bzw. - für die CL- bzw. CR-Translation verwendet werden. Dieses Tripel-Paar gehört nicht
zu einer Geraden, da ungleich Null ist. Wir benutzen darum die am Ende
der vorangehenden Seite beschriebene generalisierte Schraubung GSchraubung(a ; m) mit
.
Die Zahlen-Kombination (a ; m) stellt ein Gewinde-Quaternion dar, mit dem man bei der
Clifford-Translation das Bild einer Geraden mit dem Tripel s berechnen kann mit dem Term
.

Das CL-Parallelogramm ABCD dieser Animation hat Seiten AB und CD der Länge 30° und Seiten
AD und BC der Länge 40°. Die elliptische Größe des Winkels DAB beträgt 85,90°. Dieser Wert
tritt rechts neben dem CL-Parallelogramm auch in der Zeichnung mit Pfeilen der Länge 1 auf, die an
den Koordinaten-Ursprung angeheftet sind, gibt aber hier die euklidische Winkelgröße zwischen
einem rot-gelben und einem blau-gelben Pfeilen an. Jede dieser Farb-Kombinationen tritt hier bei vier
Pfeilen auf, wobei jeweils zwei einen Doppel-Pfeil bilden. Wir trennen die beiden Doppel-Pfeile mit
der gleichen Farb-Kombination in einen Links-Doppel-Pfeil LDP und einen Rechts-Doppel-Pfeil RDP.
Die Sortierung ergibt sich aus den (verkleinerten) Teil-Kopien unten links (L) und unten rechts (R).

Die rot-gelben Doppel-Pfeile gehören zu der Geraden AB, deren e-normiertes Tripel-Paar (u ; v) in der
obersten Zeile angegeben ist. Das Tripel-Paar (L ; R) daneben ist (bei k = 1) das Paar (u + v ; u - v).
Dabei gibt u + v das Koordinaten-Tripel der Spitze eines der beiden Pfeile vom Links-Doppel-Pfeil zu
AB an und u - v die Spitze eines der beiden Pfeile vom Rechts-Doppel-Pfeil.

Im ersten Teil der Animation wird die rot-graue Strecke PQ der Länge 30° mit Hilfe einer CR-Translation
längs AD verschoben. Für diese L-Parallele zu AB und DC ist anfangs P = A und Q = B und schließlich
P = D und Q = C. In jeder Lage von PQ ist das elliptische Lot g von einem Punkt M der Strecke AB auf
PQ als schwarz-weißer Doppelpfeil eingezeichnet. Es schneidet nicht nur PQ elliptisch orthogonal, sondern
auch AB. Darum gibt es eine Schraubung längs g, die AB in PQ abbildet. Auf der vorhergehenden Seite
' Schraubungen' wurde dazu mit Matrizen die Abbildung definiert. Die Animation
zeigt, dass hier der Betrag der Verdrehungs-Winkel und der Verschiebungs-Winkel übereinstimmen.
Die Schraubung ist folglich eine Clifford-Translation.

Bei der Bewegung von PQ bewegt sich zwar auch der zugehörige Rechts-Doppel-Pfeil, bemerkenswerter
Weise aber nicht der Links-Doppel-Pfeil. Zwei Geraden sind nämlich genau dann L-parallel, wenn ihre
Links-Doppel-Pfeile übereinstimmen. Der euklidische Winkel zwischen den Links-Doppel-Pfeilen von AB
und PQ ist also . Dazu passt, das der euklidische Winkel zwischen den Rechts-Doppel-Pfeilen
von AB und PQ gleich ist. Bei der CR-Translation von PQ wird der R-Vektor von PQ in der
Ebene gedreht, die von den R-Vektoren zu AB und DC aufgespannt wird und der L-Vektor stimmt mit
dem von AB überein. Hieraus ist das Tripel-Paar (L ; R) von PQ im Rahmen der euklidischen Geometrie
berechenbar. Damit ist (bei k = 1) ein Tripel-Paar von PQ in Plücker-Koordinaten .

Die gleiche Winkel-Beziehung zeigt sich auch an dem Winkel 85,90° zwischen AB und AD. Denn
da sich die Geraden schneiden, ist hier die Größe des Verschiebungs-Winkels gleich Null, folglich
.

Aus derTatsache, dass zwei Geraden genau dann L- bzw. R-parallel sind, wenn ihre Links- bzw. Rechts-
Doppel-Pfeile übereinstimmen, folgt die Transitivität der Relation L- bzw. R-parallel. Wenn g und h sowie
h und j also L-parallel sind, dann auch g und j.

Im zweiten Teil der Animation wird der Punkt M auf AB hin und her geschoben und die Doppel-Pfeile von
g werden angezeigt. Beide Doppelpfeile sind euklidisch orthogonal zu den entsprechenden Pfeilen von AB
und PQ. Da deren Links-Doppel-Pfeile gleich sind, kann sich LDP(g) bewegen, nicht aber RDP(g), da
RDP(AB) ungleich RDP(PQ) ist. Darum sind die Geraden g alle R-parallel.

Im dritten Teil der Animation wird um 360° gedreht und anschließend der Ablauf mit vertauschten Rollen
von AB und AD wiederholt.

In der Gleitschau findet man nach den Standbildern der Animation zu k = 1 zweiunddreißig Bilder
mit verändertem k-Wert. Das Tripel-Paar (L ; R) ist dann durch gegeben.
Die Zusammenhänge zwischen den elliptischen und den euklidischen Winkelgrößen sind die Gleichen
wie für k = 1.

Zur LR-Zerlegung :

Eine LR-Zerlegung, wie sie in der Animation für Tripel-Paare durchgeführt wurde, spielt in der Geometrie
der elliptischen Raum-Geraden auch für Paare (x ; y) reeller Zahlen eine Rolle. Wir definieren dazu die
Abbildungen LR: und ILR: , wobei ILR
die inverse Abbildung zu LR ist. k ist die zu Beginn dieser Seite genannte positive metrische Konstante.
Die Exponenten LR und ILR benutzen wir entsprechend auch für Tripel-Paare. Mit den Bezeichnungen
und
für gilt also .

Wenn j und j' zueinander polare Achsen der beiden Geraden g und h sind, dann bildet die auf der
vorangehenden Seite ' Schraubungen' definierte Abbildung bei geeigneten
Winkelgrößen g in h ab, wobei wir als Drehungs-Winkel und als Verschiebungs-Winkel betrachtet
haben. Die Abbildung bewirkt das Gleiche bei vertauschter Rolle von und .
Die Unterscheidung von Drehungs- und Verschiebungs-Winkel ist also nur in Bezug auf eine bestimmte
Achse sinnvoll.

Wenn (s ; t) und (u ; v) Tripel-Paare von g und h sind, können und mit dem Zahlen-Paar
(fg((s;t);(u;v)) ; gg((s;t);(u;v))) berechnet werden, wobei jedoch die Zuordnung zu einer Achse unklar
bleibt. Man führt dabei folgendermaßen die elliptische Maß-Bestimmung mit Hilfe der LR-Zerlegung
auf eine euklidische zurück: Sei (a;b) bzw. (c;d) das LR-Bild von (s;t) bzw. (u;v). Dann ist
.

Um und in Beziehung mit den euklidischen Winkeln zwischen a und c bzw. b und d zu bringen, ist eine
Multiplikation für Zahlen-Paare nützlich, die für hyperbolische Raumgeraden mit k = -1 die Multiplikation
komplexer Zahlen ergibt: . Zahlen-Paare mit dieser
Multiplikation und der komponentenweisen Addition werden 'ano(r)mal-komplexe Zahlen' genannt. Es ist
üblich das Paar (0 ; 1) mit j zu bezeichnen, analog der Verwendung der imaginären Einheit i bei komplexen
Zahlen. Dann gilt , und .
heißt 'zu konjugiert', analog wie bei komplexen Zahlen. Unter der 'Norm' von
verstehen wir .

Für anomal-komplexen Zahlen gelten das Assoziativ-Gesetz, Distributiv-Gesetz und das Kommutativ-Gesetz.
Allerdings gibt es nicht zu jeder Zahl ein Zahl n mit . Denn genau
die anomal-komplexen Zahlen mit der Norm Null haben kein multiplikatives Inverses. Dies sind die Zahlen
mit der Form und . Diese Elemente sind alle Nullteiler, denn
. Im Fall gilt .

Das einer elliptische Raumgeraden zugeoerdnete Tripel-Paar kann man in ein
Tripel anomal-komplexer Zahlen umschreiben, analog zur Benutzung dualer
Zahlen für euklidische Raumgeraden (siehe die Seite 'euklidische Raumgeraden> Höhen im 6-Rechteck').
Wenn man dann in umschreibt, kann
diese anomal-komplexer Zahl durch folgenden Term berechnet werden:


Bei den euklidischen Raumgeraden kann man zur Berechnung einer gemeinsamen Orthogonalen zweier
Geraden das Kreuz-Produkt für Tripel dualer Zahlen verwenden. Dies Verfahren ist auch für elliptische
Raumgeraden g zu s und h zu u wirksam, wenn man die duale Zahl durch j ersetzt. Es gilt dann also


.
Wenn die Norm von größer als Null ist, kann man das Tripel zu
normieren, um ein Geraden-Tripel der Achse von g und h zu erhalten. Die Wurzel aus einer anomal-
komplexen Zahl wird nur definiert, falls ihre Norm größer als Null ist. Dann hat für
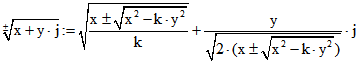für beide Vorzeichen das Quadrat .

Für anomal-komplexen Zahlen definieren wir Funktionen cos und sin unter Verwendung der
Kosinus- und Sinus-Funktion für reelle Zahlen in folgender Weise:
und .
Wenn k kleiner als Null ist, gilt eine entsprechende Formel. Sie entsteht dadurch, dass man j hier durch
die imaginäre Einheit i der komplexen Zahlen ersetzt und im Term der rechten Seite durch .
Dann gilt wie bei der Kosinus- und Sinus-Funktion für reelle oder komplexe Zahlen
und .
Für den Drehungs-Winkel und den Abstands-Winkel zwischen den Geraden g und h
mit e-normierten Tripel-Paaren (s ; t) bzw. (u ; v) und den LR-Bildern (a;b) bzw. (c;d) gilt
. Daraus folgt
.

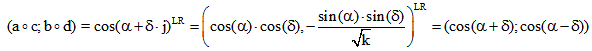Die anomal-komplexen Zahlen erlauben eine analoge Darstellung für die Matrix einer elliptischen
Schraubung, wie sie am Schluss der Seite ' Kugelviereck 2' für hyperbolische Schraubungen
angegeben wird. Dazu schreiben wir das e-normierte Tripel-Paar (s ; t) der Geraden g in der Form
. Sei die Matrix aus vier Zeilen und Spalten mit viermal
1 = (1 ; 0) in der Hauptdiagonalen und sonst nur das Paar 0 = (0 ; 0) und . Damit
definieren wir 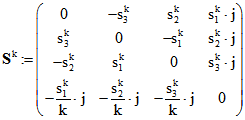und .
sei die Matrix, die aus dadurch entsteht, dass jede Komponenten durch die dazu konjugierte
Zahl ersetzt wird. Dann wird ein Punkt-Quadrupel bei der Schraubung mit dem Drehungs-Winkel
und dem Abstands-Winkel durch die Matrix abgebildet.

Die Komponenten von sind Zahlenpaare, auf die wir die LR-Zerlegung anwenden. Die Ergebnis-Matrix
aus Zahlenpaaren nennen wir . Die Matrix, die aus den linken bzw. rechten Komponenten
dieser Paare ergibt, nennen wir bzw. . Zur Beschreibung dieser Matrizen benutzen wir
die Abkürzung .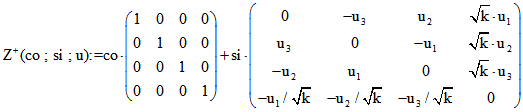
sei die Matrix, die durch Ersetzen von durch entsteht. Damit gilt:

und .

Wenn (s;t) Tripelpaar der Geraden g ist, gilt
und
.

Für Punkt-Quadrupel p und q ist
.

Die Plus-matrix bzw. Minus-Matrix ist die Matrix einer CR-Translation bzw.
CL-Translation für Punkt-Quadrupel, falls die Determinante ist. Die dazu
inverse Matrix ergbt sich, wenn man si durch -si ersetzt und durch die Determinante teilt. Die Verkettung
zweier Plus-Matrizen ist eine Plus-Matrix. Analoges gilt für die Minus-Matrizen. Jede Plus-Matrix ist mit
jeder Minus-Matrix vertauschbar, ohne dass sich das Produkt ändert. Für Plus-Matrizen (Minus-Matrizen)
gilt dies nur wenn ihre Tripel proportional sind.

Das Quaternionen-Produkt zweier Quadrupel stimmt mit und
überein. Die Bilder eines Punktes bei Plus- oder Minus-Matrizen mit gleichem u,
aber verschiedenen Parametern co oder si liegen auf einer Geraden.

Die Tatsache, dass die Plus- und die Minus-Matrizen stets vertauschbar sind, hat eine bemerkenswerte
Konsequenz für die Struktur der Gruppe, die von allen Schraubungen des elliptischen Raums erzeugt
wird. Denn wenn man auf die Funktion ILR anwendet. ergibt sich als Linearkombination
in der Form , woraus folgt.. Schaltet man mehrere
dieser Schraubungs-Matrizen hintereinander, so kann man alle Plus-Matrizen durch Vertauschungen nach
vorne schieben, ohne die Wirkung für Punkt-Quadrupel zu verändern. Daraus folgt, das die Gruppe, die
von allen Schraubungen des elliptischen Raums erzeugt wird, isomorph ist zum direkten Produkt zweier
Exemplare der Gruppe SO(3), die von den Drehungen um Ursprungs-Geraden erzeugt wird.