Es lebe die Geometrie!

Antiparallele Schnitte beim Tetraeder

->Pdf-Datei https://www.vivat-geo.de/Pdf-Dateien/Tetraeder.pdf

Unter dem P-Trieder eines Tetraeder-Eckpunktes P verstehen wir das unendliche Polyeder, das von den
drei Seitenebenen durch P eingeschlossen wird. Es ist also die Vereinigungsmenge der Punktemengen aller
Verbindungsgeraden von P mit einem anderen Punkt des Tetraeders. T sei die Tangential-Ebene an die
Umkugel des Tetreaders im Punkt P. Ein 'antiparalleler' P-Schnitt ist das Schnitt-Dreieck einer Ebene E mit
dem P-Trieder, wobei E parallel zu T ist, aber nicht mit T zusammenfällt. E ist antiparallel zu der Ebene der
Seitenfläche des Tetraeders, in der P nicht liegt (siehe dazu die zweite Animation dieser Seite). Wir folgen
damit der Bezeichnung von Joseph Neuberg (1840-1926) in seinem Buch
'Memoire sur le Tetraedre, Hayez Brüssel 1884'.

Tetraeder haben die merkwürdige Eigenschaft, dass nicht nur alle antiparallelen P-Schnitte euklidisch
ähnliche Dreiecke sind, sondern auch alle antiparallelen Q-Schnitte zu allen antiparallelen P-Schnitten
ähnlich sind, wobei Q ein von P verschiedener Eckpunkt ist, obwohl das Q-Trieder eine ganz andere
Form als das P-Trieder haben kann. Die folgende Animation stellt diesen eigenartigen Sachverhalt dar.

Zu dem Tetraeder ABCD sind die antiparallelen Schnitte zu den vier Eckpunkten so gelegt worden,
dass die Schnitt-Dreiecke nicht nur ähnlich, sondern sogar kongruent sind, folglich entsprechende
Kantenlängen gleich sind. Die Färbung einer Kante eines P-Schnitt-Dreiecks stimmt mit der Farbe
des Tetraeder-Eckpunktes überein, welcher nicht in der Seitenfläche des Tetraeders durch P und
diese Kante liegt. Darum haben Schnitt-Kanten mit gleicher Länge nicht die gleiche Farbe.

Der doppelt umkreiste Punkt in der Mitte des Tetraeders ist das Zirkum-Zentrum O der Umkugel des
Tetraeders. Jedes kleine farbige Dreieck markiert den Schnittpunkt der Verbindungs-Geraden von O
mit A, B, C oder D und dem zugehörigen antiparallelen Schnitt-Dreieck. Diese Gerade ist euklidisch
orthogonal zum Schnitt-Dreieck.

Das Tripel (0,301 ; 0,414 ; 0,277) der Schnitt-Kantenlängen ist proportional zu .

Die Quadrupel der antiparallelen Schnitt-Ebenen zu A, B, C und D sind die Zeilen der Matrix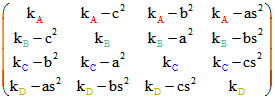
,
wobei die Konstanten mit den Indizes A, B, C und D proportional zum Abstands der Schnitt-Ebene zu
diesen Eckpunkten sind mit dem dem Kehrwert des Kugel-Durchmessers als Proportionalitäts-Konstant.
Man erkennt hier die auf der Seite ' Monge' definierte Maß-Matrix G als Summand. DieSchnitt-Dreiecke
sind kongruent genau dann, wenn das Quadrupel proportional zu
ist . Die Eckpunkte der Schnitt-Dreiecke sind





Die Seitenlängen sind dann proportional zu . gehört dabei zu der Seite, die dem
jeweils ersten Eckpunkt des Dreieck gegenüber liegt.

Die Animation zeigt, wie ein antiparalleler D-Schnitt sich als Schnitt der Kanten-Geraden durch D
mit einer Kugelfläche K ergibt. Das Zentrum M von K befindet sich zunächst im Mittelpunkt der
Umkugel des Tetraeders ABCD und wird anschließend orthogonal zur Seite ABC verschoben,
wobei A, B und C stets Punkte auf K sind.

Vor dem Rückweg des Zentrums M von K in Richtung des Mittelpunkts der Umkugel wird die
Gegen-Kugel von K durch Doppel-Pfeile angezeigt. Dies ist die Kugel durch D und die Eck-Punkte
des D-Schnitts. Ihr Zentrum bildet mit M, D und dem Mittelpunkt der Umkugel ein Parallelogramm.
Ihre Tangential-Ebene in D ist parallel zur Ebene ABC, ist also antiparallel zu der Tangential-Ebene
von K in D, die beim Rückweg durch ein Dreieck angedeutet ist, das durch Streckung des D-Schnitts
entsteht.

Es zeigt sich hier, wie die bezeichnung 'antiparallel' zustande kommt. Denn wenn die Geraden AD und
BD von einer Geraden durch Az und Bz gesczhnitten wird, die parallel zu A B ist, dann ergänzen sich
die Winkel AAz Bz und AzAB sowie BBzAz und AzBzB zu 180°. Wenn dagegen AzAB und BBzAz
sowie ABBz und BBz Az sich zu 180° ergänzen, dann liegen die vier Punkte A, B, Bz, Az auf einem Kreis.

Das erste Bild dieser Animation zeigt den Schwerpunkt S und im Innern des kleinen gelben Dreiecks
den Symmedian-Punkt Y des Seiten-Dreiecks ABC und die entsprechende Zeichnung im antiparallelen
D -Schnitt. S und Y sind zueinander isogonal konjugiert. Das bedeutet, dass Ihre Verbindungs-Gerade
mit jedem Eckpunkt des Dreiecks spiegelbildlich zur Winkelhalbierenden liegt. Dies ist durch die
Gleichheit der Größen von den markierten Winkeln an den Ecken erkennbar.

Der D -Schnitt wird in Richtung der Seite ABC parallel verschoben. Wenn dabei der Schwerpunkt diese
Seitenfläche erreicht, wird dort ein Punkt-Markierung in Form eines gelben Dreiecks abgelegt. Wir nennen
den zugehörigen Punkt Y2. Man sieht, dass dies nicht der Schwerpunkt von ABC ist. Es ist im Allgemeinen
kein Dreiecks-Zentrum von ABC im Sinne der ' Enzyclodedia of Triangle Centers ETC'. Das ist anders
beim Symmedian-Punkt des D -Schnitts. Wenn er die Seite ABC erreicht, liegt dort der Symmedian-Punkt
Y von ABC . Der Symmedian-Punkt ist in dieser Hinsicht ein Ausnahme-Punkt. Wir nennen die Gerade DY
'Symmedian-Gerade zu D' und die Gerade DY2 'Ko-Symmedian-Gerade zu D'.

Nach der Bewegung des D -Schnitts in umgekehrter Richtung und einer Drehung des Tetraeders wird der
Vorgang mit einem A-Schnitt wiederholt. Es zeigt sich dabei, dass die Symmedian-Gerade zu D die
Ko-Symmedian-Gerade zu A schneidet und entsprechend die Ko-Symmedian-Gerade zu D auch die
Symmedian-Gerade zu A.

Die Symmedian-Geraden zu den Tetraeder-Eckpunkten A, B, C und D haben die baryzentrischen
Plücker-Koordinaten




Die Plücker-Koordinaten der Ko-Symmedian-Geraden ergeben sich daraus durch die Ersetzung

Das erste Bild der Animation zeigt, dass die vier Symmedian-Geraden des Tetraeders ABCD die vier
Ko-Symmedian-Geraden schneiden. Darum gehören sie zu den beiden Regulussen eines Hyperboloids
H, das im Folgenden dargestellt wird. Im ersten Bild ist dazu die magentafarbene Ellipse gezeigt, die sich
als Schnitt-Kurve von H mit einer Symmetrie-Ebene ergibt. H ist punktsymmetrisch zu dem gleichfarbigen
Symmetrie-Punkt Z der Ellipse.

Das erste Bild der Animation wird vergrößert, um das Viereck KLMN besser erkennbar zu machen, mit
dem der Punkt Z konstruiert werden kann, analog wie beim Höhen-Hyperboloid auf der Seite ' Höhen 2'.
KL bzw. MN ist die Symmedian-Gerade zu A bzw. C und LM bzw. NK die Ko-Symmedian-Gerade
zu B bzw. D. Das Hyperboloid ist eindeutig bestimmt, wenn neben dem Viereck KLMN aus Geraden,
die auf dem Hyperboloid liegen, noch eine Teilverhältnis-Konstante tvk gegeben ist (siehe dazu die Seite
' Ceva'). tvk kann hier berechnet werden nach der Formel
.
Bei gegebenen Punkten K, L, M, N und Z ist tvk ablesbar. Denn Z teilt die Strecke zwischen den
Mittelpunkten von KM und LN im Verhältnis tvk.

Auf der Seite ' Höhen 1' wird eine Matrix F angegeben mit der Eigenschaft, dass eine Ebene mit dem
baryzentrischen Quadupel e genau dann Tagenten-Ebene von H ist, wenn . Dabei ist
ein (unnormiertes) baryzentrisches Quadrupel von Z. Es ergibt sich hier das Quadrupel





Die vier Symmedian-Geraden haben genau dann einen gemeinsamen Punkt, nämlich Z, wenn gilt:
. Das Tetraeder ABCD wird dann 'isodynamisch' genannt. Die antiparallelen
Schnitte sind dann gleichseitige Dreiecke und Symmedian-Geraden und Ko-Symmedian-Geraden
fallen zusammen. Definiert man dann , , und , ergibt
sich , , , , und und
der gemeinsame Punkt Z hat das (unnormierte) baryzentrische Quadrupel . Es ist
nicht klar, ob die Zahlen ra, rb, rc und rd einen geometrischen Sinn als Kugel-Radien haben.


Joseph Neuberg hat in dem oben genannten Text noch einen zweiten Tetraeder-Schnitt erwähnt, der
geometrisch interessant ist. Er soll in der folgenden Animation dargestellt werden.

Das erste Bild zeigt das Prinzip des Schnitts an Hand des D-Schnitts A ' B ' C ' . Da A ' auf der
Kante DA liegt, gibt es zu den kartesischen Tripeln d und a von D und A eine Zahl s mit der
Eigenschaft dass für das kartesische Tripel a' von A ' gilt: . Dabei ist
. Wir nennen s 'kartesischen Parameter'. Das Tripel der kartesischen Parameter
von A ', B ' und C ' wird so gewählt, dass es proportional zu dem Tripel der Quadrate der Flächeninhalte
von den Seiten-Dreiecken des D-Trieders ist, die A ', B ' bzw. C ' gegenüber liegen. Für A ' ist das also
die Seite DCB . Im Dreieck A ' B ' C ' sind der Schwerpunkt S und die Seitenhalbierenden eingezeichnet.

In der ersten Phase der Animation wird der D-Schnitt parallel verschoben bis S auf die Seite ABC trifft
und der Punkt dort markiert. Beim Rückweg in der zweiten Phase werden die Flächeninhalte der Seiten
des D-Trieders und deren dunkler gefärbten Teil-Dreiecke angezeigt. Die Produkte der roten, der grünen
und der blauen Zahlen stimmen überein.

Das folgende Standbild mit dem D-Schnitt und dem C -Schnitt zeigt, dass sich für alle vier Schnitte die
Spuren des Schwerpunkts S in einem Punkt L schneiden. Er wird nach Emile Lemoine (1840-1912)
Lemoine-Punkt genannt. Die kartesichen Koordinaten von L sind oben links angezeigt. Das Quadrupel
aus den Quadraten der Flächen-Inhalte der Seiten-Dreiecke von ABCD ist (unnormiertes) baryzentrisches
Quadrupel von L. Die Summe der Quadrate der Abständen des Punktes L von den Seiten-Dreiecken ist
kleiner als die analoge Summe für irgendeinen anderen Punkt im Innern von ABCD. Dies wird der letzten
Phase der Animation mit dem Schwerpunkt von B-Schnitten verdeutlicht.

Das normierte Quadrupel der baryzentrischen Koordinaten eines Punktes P im Innern von
ABCD besteht aus den Quotienten der Volumen der Tetraeder PBCD , APCD , ABPD bzw. ABCP und
ABCD. Wenn das Quadrupel der Inhalte der Seiten-Dreiecke bezeichnet, V das Volumen von
ABCD und das Quadrupel der Abstände P von den den Seiten-Dreiecken, dann gilt nach
der Formel für das Volumen eines Tetraeders und .
Man errechnet für die Summe der Quadrate der Abstände




ist darum für einen Punkt P im Innern von ABCD genau dann minimal, wenn die Summe der Quadrate
der Differenzen Null wird, also wenn diese Differenzen selbst alle gleich Null sind. Das
bedeutet, dass proportional zu ist, es also eine Zahl ungleich Null gibt mit
. Daraus folgt und P ist der
Lemoine-Punkt, für den also die Summe der Quadrate der Abstände von den
Seiten-Ebenen des Tetraeders minimal ist.
(Wegen der Normierung von p ist und .)

Man kann diese Überlegung auch auf einen Punkt P außerhalb des Tetraeders übertragen. Dann ist mindestens
eine Komponente negativ, z. B die erste. Dann verstehen wir unter den mit einem Minus-Zeichen versehenen
Abstand von der Seiten-Ebene, die A nicht enthält. Es ergeben sich dann sieben weitere Punkte, für welche die
Summe der Quadrate der Abstände von den Seiten-Ebenen ein relatives Minimum ergeben, nämlich die Punkte
mit folgenden unnormierten baryzentrischen Quadrupeln:



Die entsprechende Überlegung kann man bei einem Dreieck an Stelle eines Tetraeders durchführen, wobei
die Flächen-Inhalte durch Seiten-Längen ersetzt werden. Die Summen mit vier Quadraten werden auf drei
reduziert und auch die Summe der sechs Quadrate von Differenzen. Der Symmedian-Punkt Y ist der Punkt
im Innern des Dreiecks mit dem (unnormierten) baryzentrischen Tripel aus den Quadrate der Seiten-Längen.
Die Rechnung zeigt, dass für Y die Summe der Quadrate der Abstände von den Seiten des Dreiecks minimal
ist. Y wird darum auch als Lemoine-Punkt des Dreiecks bezeichnet.



.