Es lebe die Geometrie!

Einschaliges Hyperboloid 2

Auf dieser Seite wird das Standard-Viereck ABCD variiert, mit dem nach der auf der Seite ' Ceva'
beschriebenen Konstruktion ein Hyperboloid erzeugt wird.

In der Animation werden die Punkte B und D symmetrisch zur xy-Ebene um die Achse AC gedreht
und das Hyperboloid zum Basis-Viereck ABCD und der Teilverhältnis-Konstante tvk = 2 gezeigt.
Nach dünnen Linien für die Regulus-Geraden in der ersten Periode, werden diese in der zweiten als
Stäbe dargestellt, in hellblau für die Vorderseite und in gelb für die Rückseite. Bei der Drehung
gleiten die Stäbe schneidender Regulus-Geraden so aneinander vorbei, als seien sie nur mit einer
Schlaufe miteinander verbunden.

Ausgehend von dem gleichen Viereck ABCD wie in der vorangehenden Animation werden hier bei
der Teilverhältnis-Konstanten tvk = 2 die Eckpunkte auf Ursprungs-Geraden in den am Ursprung
gespiegelten Punkt verschoben, und zwar erst A, dann C, dann B und schließlich D. Dabei wurden
Schnittkurven des Hyperboloids mit Symmetrie-Ebenen eingezeichnet. Die Vektoren vom Mittelpunkt
des Hyperboloids zu gemeinsamen Punkten zweier dieser Sschnittkurven haben die Richtungen
der Eigenvektoren, die in gleicher Farbe unten rechts im Bild angegeben sind. Die beiden Vektoren,
deren Spitzen auf Schnittpunkte zweier Schnittkurven treffen, sind euklidisch orthogonal und auch
orhogonal zum dritten Vektor, der vom Mittelpunkt in Richtung der Symmetrie-Achse des Hyperboloids
zeigt. Dieser hat die gleiche Richtung wie der dritte Eigenvektor. Jeder der drei Vektoren ist euklidisch
orthogonal zu einer Symmetrie-Ebene.

Die Berechnung der Eigenvektoren wird unten erklärt.

Nach dem ersten Teil der Animation mit Zeichnungen der Regulus-Geraden wird beim Zurückschieben
der Punkte in umgekehrter Reihenfolge das zugehörige Hyperboloid in Kachel-Ansicht gezeigt.

Wie auf der Seite ' Ceva' bezeichnen wir das kartesiche Quadrupel mit , das entsteht, wenn man das
Koordinaten-Tripel a von A durch die vierte Komponente 1 ergänzt, und verfahren mit b, c und d analog.
sei das Quadrupel (x ; y ; z ; 1). Der zugehörige Punkt X liegt genau dann auf der Quadrik QH, die mit
der Teilverhältnis-Konstanten tvk im Viereck ABCD konstruiert wird, wenn gilt:
(*) .
Für das Standard-Viereck
ist dies die Gleichung , für tvk = 2 also
. Mit Hilfe von symmetrischen Matrizen lassen sich diese Gleichungen in
(**) der Form 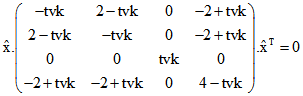bzw.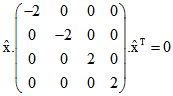
schreiben, wobei die zur Spalte transponierte Zeile (x ; y ; z ; 1) bedeutet und wie die Zeile als Matrix
verstanden wird. Die besondere Form der Matrix zu tvk = 2, dass nämlich außerhalb der Hauptdiagonalen
nur Nullen vorkommen, lässt erkennen, dass die Koordinaten-Ebenen x = 0, y = 0 und z = 0 in diesem Fall
Symmetrie-Ebenen von QH sind. Die Tatsache, dass in dieser Diagonal-Matrix zwei der vier Zahlen in der
Hauptdiagonalen positiv und die zwei anderen negativ sind, kennzeichnet die Quadrik als Hyperboloid
oder hyperbolisches Paraboloid.

Erweitert man das Koordinaten-Tripel x nicht zum Quadrupel (x ; y ; z ; 1), sondern zu (x ; y ; z ; 0) , und
setzt dieses Quadrupel für in die Gleichung (*) ein, dann sind die Lösungen die Quadrupel, die man als
'unendlich ferne Punkte' der Quadrik ansieht. Sie gehören zu der 'projektiven Erweiterung' des affinen Raums
der Koordinaten-Tripel.

Für jedes Viereck ABCD mit nicht komplanaren Eckpunkten und einer Teilverhältnis-Konstanten tvk
ungleich Null bezeichnen wir die Matrix in der Zeile (**) mit Fp. Es gilt also
.
Die Gleichung beschreibt für tvk ungleich Null und 1 ein Hyperboloid und ein hyperbolisches
Paraboloid für tvk = 1. Die auf der Seite ' Ceva' eingeführte Matrix F ist für ein beliebiges Viereck
ABCD mit nicht komplanaren Eckpunkten
und .
Die Matrix F bzw. Fp bestimmt eine Bilinearform f bzw. fp für die H-Orthogonalität von Ebenen bzw.
H-Polarität von Punkten. Im Sinne dieser nicht-euklidischen Maß-Bestimmung sind Ebenen D und E
mit den Quadrupeln d bzw. e H-orthogonal, wenn gilt. Punkt X und Y sind
zueinander H-polar, wenn . Die Symmetrie-Ebenen sind sowohl euklidisch
als auch H-orthogonal.

Der (endliche) Mittelpunkt Z von QH, zu dem die Quadrik punktsymmetrisch ist und der auf allen
Symmetrie-Ebenen liegt, hat im Fall tvk ungleich 1 das Quadupel [0 ; 0 ; 0 ; 1].F . Dabei ist die vierte
Komponente möglicherweise ungleich Eins. Beim Hyperboloid ist diese Zahl im Gegensatz zum
hyperbolischen Paraboloid ungleich Null. Man teilt alle vier Komponenten durch die vierte, um das
Koordinaten-Tripel von Z zu erhalten. Das Quadrupel [0 ; 0 ; 0 ; 1] gehört zu der unendlich fernen
Ebene, deren H-Pol Z ist. Für jedes Viereck ABCD teilt Z die Strecke vom Mittelpunkt von AC zum
Mittelpunkt von BD im Verhältnis -tvk.


Die Zahlen-Tripel im Bild der Animation unten rechts geben die Eigenvektoren der reduzierten
Matrix Fpred an, die entsteht, wenn man bei Fp die vierte Zeile und Spalte weglässt. Jeder dieser
Eigenvektoren v hat die Eigenschaft, dass es zum Vektor v.Fpred eine Zahl r gibt, so dass
gilt. Der 'Eigenwert' r ist jeweils neben dem zugehörigen Eigenvektor in der
Animation angegeben.

Wenn ein Vektor v Eigenvektor zu einem Eigenwert r ist, gilt dies auch für jeden Vektor, der aus
v durch Multiplikation mit einer reellen Zahl s ungleich Null entsteht. Die im Bild angegebenen
Eigenvektoren wurden auf die Länge 1 normiert.

Durch die Matrix Fpred sind die drei Eigenwerte eindeutig bestimmt. Wenn man die Matrix Fp
mit einer reellen Zahl s multipliziert, gehört ein Quadrupel genau dann zu einem Punkt von QH,
wenn gilt. Die Eigenwerte der Matrix, die aus Fpred durch
Multiplikation mit s entsteht, ergeben sich aus denen von Fpred ebenfalls durch Multiplikation
mit s. Darum sind nur die Quotienten dieser Eigenwerte für das Hyperboloid cherakteristisch.

Es gibt einen Zusammenhang zwischen den Eigenwerten und den Hauptachsen-Abschnitten von den
Kegelschnitten der Symmetrie-Ebenen. r1 und r2 seien Eigenwerte mit gleichem Vorzeichen zu den
Eigenvektoren, die orthogonal zu den Symmetrie-Ebene E1 bzw. E2 sind. Die zugehörigen Kegelschnitte
K1 und K2 sind dann Hyperbeln, die mit dem elliptischen dritten Kegelschnitt K3 gemeinsame
Scheitelpunkte S1 und S2 mit den Abständen d1 und d2 von Z haben. Dann ist .
Der dritte Eigenwert r3 bestimmt mit r1 bzw. r2 für K1 bzw. K2 das Verhältnis der imaginären
zur reellen Halbachse.

Wenn man das Koordinatensystem so legt, dass A in Ursprung liegt und die Punkte B, C und D
in den Einheits-Punkten auf der x- , y- bzw. z-Achse liegen, dann liegt ein Punkt (x ; y ; z) genau dann
auf QH, wenn gilt. Dazu gehören die Matrizen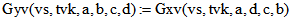
und 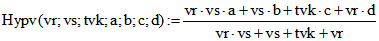, sodass also
ist. Das Koordinatensystem ist dann möglicherweise nicht rechtwinklig.
a, b, c und d seien die Tripel von A , B, C und D ím ursprunglichen System und M die Matrix mit den Zeilen
a-d, b-d und c-d.. In diesem System ist dann , wobei das hochgestellte T zum
Transponieren der Matrix (Vertauschen von Zeilen und Spalten) führt. sei die Matrix, die aus M
dadurch entsteht, dass man das Tripel a als vierte Zeile hinzufügt und die entstehende Matrix um die vierte
Spalte ergänzt. Dann ist die Matrix F, welche die H-Orthogonalität von Ebenen bestimmt, durch
gegeben.

Die Eigenwerte von Fpred sind die Lösungen w der 'charakteristischen Gleichung'
zu Fpred. Dabei ist I die Matrix mit drei Einsen in der Hauptdiagonalen und sonst Nullen. Dies ist eine
Gleichung der Form . Dabei ist k2 die Spur von Fpred, also die Summe der
Zahlen der Haupt-Diagonalen. k1 ist die Spur der Matrix der Minoren zu Fpred, also der Determinanten der
Matrizen, die entstehen, wenn man eine Zeile und eine Spalte von Fpred streicht. Diese Unter-Determinante
setzt man an die Kreuzungs-Stelle der Zeile und Spalte. k0 ist die Determinante von Fpred.

Den Zusammenhang zwischen den Eckpunkten A , B, C und D des Basis-Vierecks und den Vorzahlen der
charakteristischen Gleichnung kann man folgendermaßen herstellen: Für das euklidische innere Produkt bzw.
Kreuz-Produkt zweier Vektoren benutzen wir das Zeichen bzw. . Die Determinante von M sei mit det
bezeichnet. q sei das Quadrat der euklidischen Länge des Vektors . Dann ist


.
Die Eigenwerte, die sich mit diesen Vorzahlen ergeben, wurden in der Animation mit multipliziert.


Zur Bestimmung der Scheitelpunkte der Kegelschnitte, die von den Symmetrie-Ebenen aus der Quadrik
ausgeschnitten werden :

Sei zunächst tvk<>1, also QH ein Hyperboloid. Dann gibt es drei Symmetrie-Ebenen. Diese sind euklidisch
orthogonal zu den Eigenvektoren und enthalten den Mittelpunkt Z. Eine dieser Ebenen hat eine Ellipse als
Schnittkurve. Wir nennen diese E0. Die anderen beiden Ebenen E1 und E2 schneiden aus QH Hyperbeln.
Sie gehören zu Eigenwerten von Fpred, die entweder beide positiv oder beide negativ sind. Jede der Ebenen
E0, E1 und E2 hat den unendlich fernen Punkt der Geraden als Pol, die durch Z in Richtung des zur Ebene
euklidisch orthogonalen Eigenvektors bzw. bzw. verläuft. Diese Gerade ist für E0 die Symmetrie-
Achse des Hyperboloids, die keinen Punkt mit QH gemeinsam hat. Für E1 (E2) ist es eine Symmetrie-
Gerade, die QH in gemeinsamen Scheitelpunkten S2, und S2' (S1 und S1') des Kegelschnitts zu E2 (E1)
und E0 euklidisch orthogonal schneidet. Darum ist der zu E1 bzw. E2 orthogonale Eigenvektor bzw.
auch orthogonal zur Tangential-Ebene T2 bzw. T1 zu den Punkten S2 bzw. S1. Diese beiden Punkte sind
Pole von T2 und T1. Darum ergibt sich ein Quadrupel von z. B S2 dadurch, dass man ein als Matrix-Zeile
geschriebenes Quadrupel zu T2 von rechts mit der Matrix F multipliziert. Für die ersten drei Komponenten
des Quadrupels von T2 kann man die Komponenten des Eigenvektors von Fpred
nehmen, zu denen wir die vierte noch unbekannte Komponente u hinzufügen. Sei
und . Das Quadrupel zum Scheitelpunkt S2 kann in der Form mit
und geschrieben werden, wobei h Quadrupel des Hyperboloid-Zentrums Z
ist. Da das Quadrupel eines Punktes von QH ist, kann u aus folgender quadratischen Gleichung
berechnet werden :
.
Weil Quadrupel der Tangential-Ebene im Punkt S2 ist, kann man u auch aus der Gleichung
bestimmen.

Sei nun tvk = 1, also QH ein hyperbolisches Paraboloid. Dann ist , und
. Ein Eigenwert von Fpred ist darum Null, und die anderen
beiden haben unterschiedliche Vorzeichen. Es gibt zwei Symmetrie-Ebenen E1 und E2. Sie sind orthogonal
zu den Eigenvektoren und zu den Eigenwerten ungleich Null. Die Schnittgerade dieser Ebenen ist
Symmetrie-Achse des Paraboloids in Richtung des dritten Eigenvektors zum Eigenwert Null. und der
Verbindungs-Vektor des Mittelpunkts von A und C mit dem Mittelpunkt von B und D sind linear abhängig.
Die Symmetrie-Achse ist also parallel zur Geraden durch diese beiden Mittelpunkte und hat die Richtung des
Vektors a+c-b-d. Sie schneidet das Paraboloid im Punkt S von QH. Dieser ist gemeinsamer Scheitelpunkt
der Parabeln, die sich beim Schnitt von E1 und E2 mit QH ergeben. Das oben für tvk >1 angegebene Verfahren
führt dann zu einer Gleichung, bei der fp(h;h) = 0 ist, die also nur eine Lösung hat.

Die vierte Zeile der Matrix F, die für tvk <> 1 den Mittelpunkt des Hyperboloids angibt.
gehört für tvk = 1 zu dem unendlich ferne Punkt auf der Symmetrie-Achse des Paraboloids. Wir bezeichnen
ihn in beiden Fällen mit Z. Er ist ein Tangentialpunkt in der projektiven Erweiterung des Paraboloids und der
einzige unendlich ferne Punkt auf jeder der beiden Parabeln in den Symmetrie-Ebenen. Es gibt eine reelle Zahl r
ungleich Null mit . Den Punkt S, der eine Art Mittelpunkt des Paraboloids ist, aber kein Symmetrie-
Punkt, nennen wir 'Sattelpunkt'. Analog wie beim Hyperboloid gilt
. Wegen
und folgt . Wenn man also
den Eigenvektor mit u als vierter Komponente zu ergänzt, ist Quadrupel von S.