Es lebe die Geometrie!

Rechtecke mit fünf Ecken

Ein Rechteck oder Rechtseit ist ein Polygon mit lauter Innenwinkeln von 90°. In der euklidischen
Geometrie ist das Polygon dann ein Viereck. In der hyperbolischen Geometrie gibt es keine Vierecke,
die Rechtecke sind. Denn wenn man ein hyperbolisches Viereck durch eine Diagonale in zwei Dreiecke
teilt, haben beide eine Innenwinkel-Summe kleiner als 180°. Es gibt aber Rechtecke zu jeder Eckenzahl,
die größer als 4 ist. Wir betrachten hier nur Rechtecke mit 5 Ecken.

Bei allen Rechtecken schließen sich die Seiten zu vollständigen hyperbolischen 'Geraden' zusammen.

Damit es nicht zu Überlappungen von Kacheln kommt, sind nur Ketten-Schemata möglich, bei denen
ein ganzzahliges Vielfaches der Summe der darin vorkommenden Winkel-Größen 360° beträgt. Diese
Summe kann also nur 90°, 180° oder 360° betragen. Dies sind einzigen Signaturen, für die das zutrifft:
-1-2-3-4-5 , -1-2-3-45 , -1-23-45

-1432-5 , -14-32-5 , 54-321 , 5-43-21 , 5-2-3-41 , 5-23-41 , 54321 , 52341

213-5-4 , -2-1354

Diese Liste ist allerdings nur dann vollständig, wenn man Signaturen identifiziert, die dadurch auseinander
hervorgehen, dass man die Nummerierung der Kachel-Seiten zyklisch verschiebt.

Bei den ersten drei Signaturen dieser Liste kommen nur Achsen- oder Punkt-Spiegelungen vor, bei den
nächsten acht genau ein Paar von Seiten, die durch Nachbar-Bewegungen auseinander hervorgehen, und
bei den letzten beiden Signaturen gibt es zwei derartige Paare.

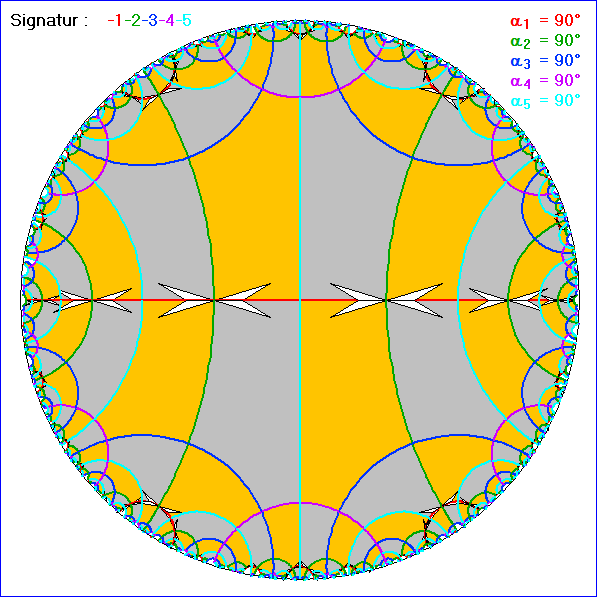
Ein 5-Rechteck kann durch eine hyperbolische Bewegung immer in eine Lage mit der Seite 1 auf der
Rechts-Achse und der Seite 5 und auf der Hoch-Achse gebracht werden. Dann ist die Seite 2 ein
Kreisbogen mit dem Mittelpunkt auf der Recht-Achse, dessen Koordinaten mit einer reelle Zahl a
durch gegeben sind. Entsprechend gibt es eine Zahl b, so dass das Zentrum des Kreisbogens
der Seite 4 der Punkt ist. Dann hat der Kreisbogen der Seite 3 das Zentrum . Im Fall
a = b ist das Rechteck symmetrisch zur Höhe auf der Seite 3. Nur für haben
alle Seiten die gleiche hyperbolische Länge.

Bild 1 der Gleitschau zeigt eine Kachelung, die aus einer Ausgangskachel mit a ungleich b allein
durch Achsen-Spiegelungen entsteht. Dabei wurden die negativ orientierten Kacheln gelb gezeichnet.


Bild 2 zeigt die gleiche Kachelung im Beltrami-Klein-Modell. Die grauen Ausgangs-Kachel hat hier
die Ecken Nummer 1 bis 5 in den Punkten , , 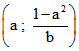, 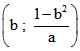und .
Das Quadrat vom Cosinus hyperbolicus der Abstands zweier Punkte und ist nach
'Die Pseudosphäre und die hyperbolische Geometrie' , Satz 24
durch 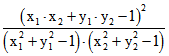bestimmt. Für die Seiten 1 bis 5 ergeben sich daraus nach
Einsetzen der Eckpunkte die Werte , , , und .


Im Bild 3 wurden die Höhen hinzugefügt. Sie schließen sich wie die Seiten zu hyperbolischen 'Geraden'
zusammen, im Gegensatz zu den Seitenmitten-Verbindungen im Bild 4. Die Bilder 5 bis 8 zeigen zeigen
Entsprechendes für gleichseitige Kacheln. Bei Bild 7 ergibt sich dabei eine neue Kachelung aus
gleichschenkligen Dreiecken und bei Bild 8 eine Kachelung mit mit regelmäßigen Vier- und Fünf-Ecken.

Die Bilder 9 und 10 gehen von der gleichen Ausgangs-Kachel wie in Bild 1 aus, jedoch mit anderen
Signaturen. Bei Bild 9 ergibt sich eine neue Kachelung aus Rechtecken mit 6 Eckpunkten, bei Bild 10
und 11 eine aus Rechtecken mit unendlich vielen Eckpunkten. Bild 11 zeigt, dass die Kacheln gleicher
Farbe auf den magentaroten Verbindungen der Mitten der Seiten 3 und 5 aufgefädelt sind. Die grauen
und gelben zusammenhängenden Flächen haben genau zwei Randpunkte auf dem Einheitskreis, nämlich
die Enden der magentaroten 'Geraden' , zu denen sich die Mitten-Verbindungen zusammenschließen.
In den Bildern 9 bis 11 ergeben sich die Winkelsummen unten links aus den Ketten-Schemen, die zu
den Signaturen gehören.

Die Kachelung zur Signatur -1432-5 wird durch Achsenspiegelungen B1 und B5 an den Seite 1 und 5
(irgendeiner Ausgangskachel K0), der Punktspiegelung B3 an der Seite 3 und Translationen B2 und B4
zwischen den Seiten 2 und 4 erzeugt. B2 bildet die Seite 4 auf die Seite 2 ab und B2 ist die Umkehr-
Abbildung davon. Da folglich diese beiden Seiten gleich lang sind, müssen die oben genannten Zahlen a
und b gleich groß sein und darum auch die Seiten 1 und 5 die gleiche Länge haben. Da alle Innenwinkel
die Größe 90° haben, ist jede Kachel achsensymmetrisch zur Winkelhalbierenden durch den Eckpunkt
Nummer 5.

Die Seite 3 steht senkrecht zu den Seiten 2 und 4. Darum ist die 'Gerade' der Seite 3 die Achse von B2.
Da Translationen zur gleichen Achse bei Vertauschung der Reihenfolge der Anwendung zum gleichen
Ergebnis führen, ist B2 nicht nur Nachbarbewegung von K0, sondern auch Nachbarbewegung von jeder
Kachel, die durch wiederholte Anwendung von B2 daraus entsteht. Diese Kacheln werden durch B2 an
der Achse 'aufgefädelt' und haben die beiden Enden der Achse als Grenzpunkte. Die Animation zeigt den
Prozess dieser 'Auffädelung' durch B2 in einer Richtung und durch B4 in der Gegenrichtung.

Bei der Signatur 5-43-21 sind gegenüber der vorherigen Signatur -1432-5 einerseits die
Achsenspiegelungen B1 und B5 durch 90°-Drehungen ersetzt worden, andererseits die
Translationen B2 und B4 durch Gleitspiegelungen. Auch hier sind darum die Seiten 2 und 4
gleich lang, also a = b und folglich die Winkelhalbierenden g durch den Punkt Nummer 5
Symmetrieachse der Ausgangskachel K0. Die Hintereinanderschaltung der Punkt-Spiegelung
an der Seitenmitte M der Seite 4 und der Spiegelung an g ist ungerade und bildet die Seite 4
auf die Seite 2 ab. Da sie also mit B2 übereinstimmt, ist die 'Lotgerade' zu M und g die Achse
von B2. Dies ist die 'Gerade' durch die Seitenmitten der Seiten 2 und 4.

Die Animation zeigt, wie durch B2 und B4 die Kacheln längs der Achse 'aufgefädelt' werden.
Von einer Kachel zur nächsten kommt man dabei durch Anwendung der Nachbar-Bewegungen
B2 oder B4 der Ausgangskachel K0. Da die Hintereinanderschaltung zweier Gleitspiegelungen
mit der gleichen Achse sich bei Änderung der Reihenfolge gleich bleibt, sind B2 und B4 nämlich
auch Nachbar-Bewegungen aller aufgefädelten Kacheln.

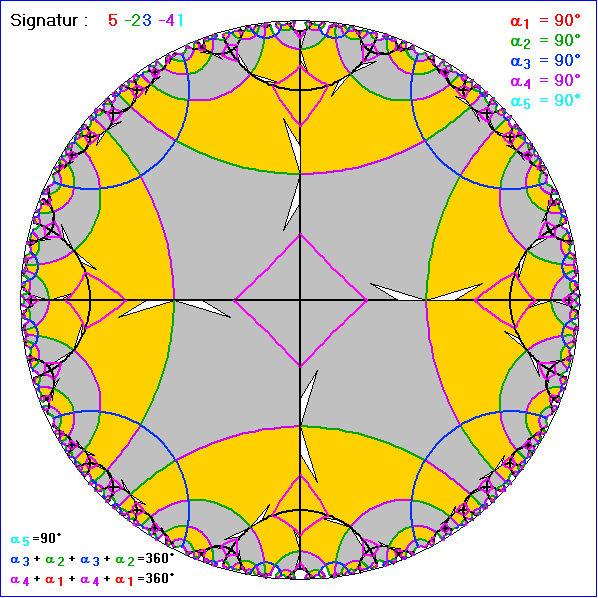
Die Signaturen
-1432-5 , -14-32-5 , 54-321 , 5-43-21 , 5-2-3-41 , 5-23-41 , 54321 , 52341
führen zu Kachelungen, die sich nur in der Lage der Pfeile unterscheiden. Die Kachelseiten schließen sich
zu vollständigen 'Geraden' zusammen, die bei all diesen Signaturen gleich sind. Auf diesen 'Geraden'
haben die Seiten aber unterschiedliche Nummern. Alle Kacheln sind symmetrisch zur Winkelhalbierenden
durch den Punkt Nummer 5.

In der Gleitschau wurden die Translations- und Gleitspiegelungs-Achsen grün eingezeichnet und die Seiten
in ihrer Farbe, wenn sie zu Punkt-oder Achsen-Spiegelungen gehören, sonst in schwarz. Die magentaroten
Vierecke entstehen durch die Verbindung der Mitten von den Seiten 1 und 5. Negativ orientierte Kacheln
wurden gelb gezeichnet.

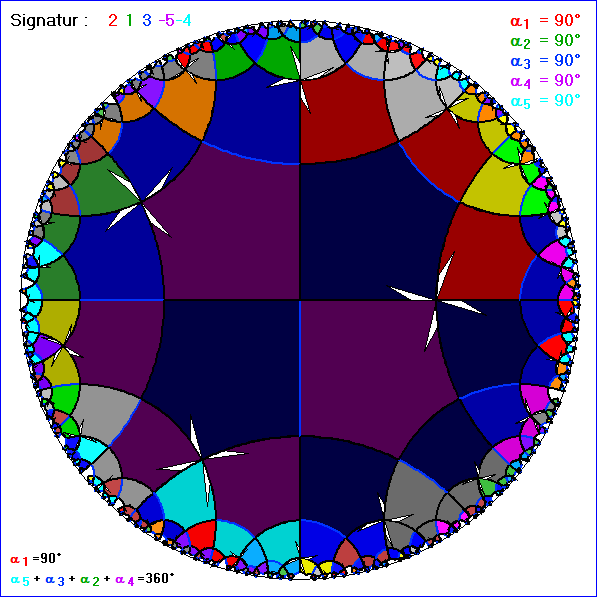
Die Signatur 213-5-4 führt nur dann zu einer Kachelung, wenn das rechtwinklige Fünfeck
gleichseitig ist. Denn B1 ist wie B2 eine 90°-Drehung um den Eckpunkt Nummer1 und B4
ist wie B5 eine Gleitspiegelung mit der Achse durch die Mitten der Seiten 4 und 5. Darum
sind die Seiten 1 und 2 wie auch die Seiten 4 und 5 gleich lang. Mit den oben angegebenen
Werten für das Quadrat des Cosinus hyperbolicus von den Seitenlängen errechnet man
daraus .

Das Bild 1 der Gleitschau zeigt die Kachelung zur Signatur 213-5-4 mit grün gezeichneten
Gleitspiegelungs-Achsen. In Bild 2 sind alle Verbindungen der Mitten aufeinanderfolgender
Seiten eingezeichnet und in Bild 3 die Verbildungen der Mitten der jeweils übernächsten Seite,
so dass Pentagramme entstehen. Diese Verbindungen fügen sich zu hyperbolischen 'Geraden'
zusammen. Bild 4 zeigt die farbliche Zusammenfassung der Kacheln mit gemeinsamen Eckpunkt
Nummer 1 zu Rechtecken mit acht Ecken.