Es lebe die Geometrie!

In- und Ex-Quadrik beim Viereck
auf der Einheits-Kugel mit nicht komplanaren Eckpunkten

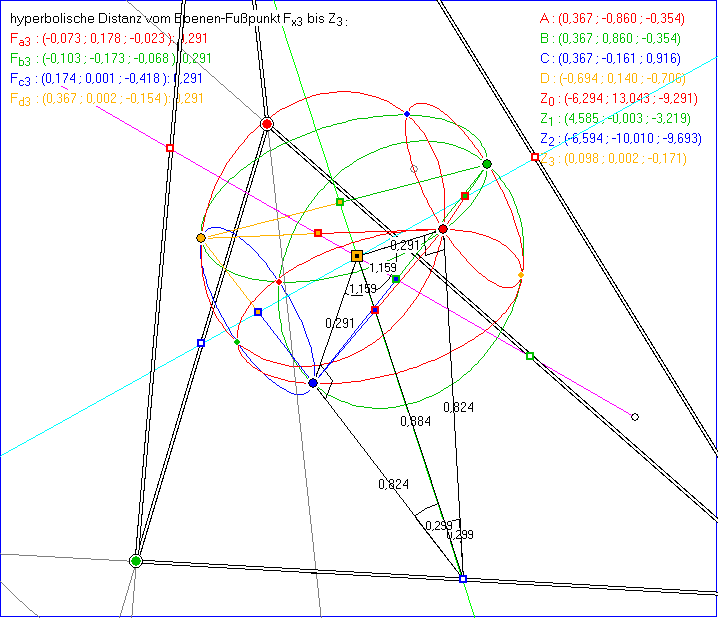
Wie auf der vorigen Seite ' Kugelviereck 1' betrachten wir auf dieser Seite ein räumliches Viereck ABCD
aus Punkten auf der Fläche der Kugel K vom Radius 1 um den Koordinaten-Ursprung. Dabei werden
hyperbolische Maße benutzt, wie sie für die Orthogonalität und für Abstände von Punkten schon auf den
vorigen beiden Seiten erklärt wurden. Grundlegend für die Berechnung ist dabei die Bilinearform
, deren zugehörige Quadratform f(x;x) genau für die Punkte
zum Koordinaten-Quadupel Null wird. Wir bezeichnen dieses Quadrupel zum Koordinaten-
Tripel mit . Z3 sei wie auf der vorigen Seite der gemeinsame Schnittpunkt dreier Achsen
gegenüberliegenden Kanten-Geraden von ABCD im Innern des zugehörigen Vierflachs. In der folgenden
Animation wird dargestellt, dass Z3 von allen Seiten-Ebenen des Vierflachs den gleichen hyperbolischen
Abstand hat. Z3 ist hyperbolischer Mittelpunkt einer Quadrik, die alle vier Seiten-Ebenen berührt. Wir
nennen sie 'In-Quadrik'. Sie hat die Form eines euklidischen Ellipsoids mit Z3 als Symmetriepunkt und
entspricht in der euklidischen Dreiecks-Geometrie dem Inkreis. Alle Punkte der In-Quadrik haben von Z3
den gleichen hyperbolischen Abstand. Mit 'Ex-Quadrik' bezeichnen wir drei Quadriken, die beim Dreieck den
Ankreisen entsprechen. Sie berühren ebenfalls alle vier Seiten-Ebenen von ABCD. Auch jede Ex-Quadrik
hat einen Mittelpunkt, zu dem alle ihre Punkte den gleichen hyperbolischen Abstand haben, nämlich einen der
Punkten Z0, Z1 und Z2 der vorigen Seite. Jeder dieser Mittelpunkte ist wie Z3 Schnittpunkt dreier Achsen
gegenüberliegenden Kanten-Geraden von ABCD . Z0, Z1 und Z2 liegen außerhalb des Vierflachs. Die
Ex-Quadiken haben die Form eines einschaligen Hyperboloids, das die Einheits-Kugel K berührt.

Die Animation zeigt das Viereck ABCD mit schwarz-weiß markierten Kanten und Achsen
gegenüberliegender Kanten in den Farben magentarot, hellgrün und hellblau, die sich im gelben
Punkt Z3 schneiden. Die Lotfußpunkte der Achse auf den Kanten sind als Quadrate gezeichnet, um
auszudrücken, dass sich hier Achse und Kante hyperbolisch orthogonal schneiden. Die Fußpunkte der
Lote von Z3 auf die Seitenebenen des Vierflachs ABCD sind in den Farben der gegenüberliegenden
Eckpunkte angegeben. Sie sind mit den Fußpunkten ihrer Lote auf dei Achsen verbunden, im ersten Bild
der Animation auch mit den Eckpunkten ihrer Seitenfläche. Die Schnittpunkte der Achsen mit der Einheits-
Kugel sind als kleine Kreise mit weißem Innern gezeichnet.

Die ersten Ansichten der Animation zeigen die Spur der Bilder der Ebenen-Fußpunkte bei hyperbolischen
Drehungen um die Achsen mit wachsendem Drehwinkel. Jedes dieser Bilder hat den gleichen Fußpunkt auf
seiner Dreh-Achse wie der Ebenen-Fußpunkt, und auch den gleichen hyperbolischen Abstand. Zu jedem
Ebenen-Fußpunkt und jeder der drei Achsen entsteht ein hyperbolischer Kreis in einer zur Achse hyperbolisch
orthogonalen Ebene. Diese zwölf Kreise liegen auf der In-Quadrik von ABCD. Im zweiten Teil der Animation
wird die Konstruktion im Raum um 360° gedreht.

Der dritte Teil startet mit lediglich vier Kreisen, die bei Drehung um die hellblaue Achse entstehen, wobei ein
blauer Kreis von einem grünen überdeckt wird und ein roter von einem gelben. Die Kreise werden dann durch
schaubenförmige Kurven ersetzt, die schließlich in den beiden Schnittpunkten der Achse mit der Einheits-Kugel
enden. Jeder Punkt einer dieser Kurven entsteht dadurch, dass auf einen Ebenen-Fußpunkt eine Abbildung
angewandt wird, die wir 'Schraubung' nennen. Sie ist eine Überlagerung einer Drehung mit einer hyperbolischen
Verschiebung . Man kann erst drehen und dann verschieben, oder auch die Dreh-Abbildung (Rotation) und die
Verschiebungs-Abbildung (Translation) in der Reihenfolge vertauschen, ohne dass sich der Ergebnis-Bildpunkt
ändert. Wenn man euklidische Maße benutzt, bleiben die Bildpunkte bei diesen Schraubungen mit gleicher Achse
und gleichem Urbild-Punkt auf einem Zylinder mit der Achse als Mittellinie. Bei hyperbolischen Maßen ergibt
sich statt des Zylinders ein euklidisches Ellipsoid. Denn die Abstände der Bildpunkte bei der hyperbolischen
Schraubung von der Achse sind alle gleich, aber der euklidische Abstand nimmt bei Annäherung an die Kugel-
Fläche bis zum Grenzfall Null ab.

Der vierte Teil der Animation beginnt, wenn die Schrauben-Kurve die weiß-gefüllten Endpunkte auf der Kugel
(fast) erreicht hat. Anschließend werden die Rotations-Anteile der Schraubungen reduziert, so dass im Endeffekt
nur die Translations-Anteile übrigbleiben. Es ergeben sich die vier euklidisch elliptischen Kurven, deren Punkte
den gleichen Abstand von der Achse haben. Der fünften Teil der Animation zeigt alle zwölf Kurven, deren Punkte
dadurch entstehen, dass ein Ebenen-Fußpunkt längs einer der drei Achsen durch Z3 verschoben wird. Sie werden
dann um 360° gedreht, um ihre räumliche Lage deutlicher zu machen.

Die Zeichnungen der Gleitschau sollen deutlich machen, inwiefern die In-Quadrik dem Inkreis der
euklischen Dreiecks-Geometrie entspricht, insbesondere auch im Hinblick auf Winkel-Beziehungen.
Dabei ordnen wir einem Ebenen-Paar (D ; E) des dreidimensionalen projektiven Raums als Wert des
Winkel-Maßes den Abstand ihrer Pole zu. und seien Koordinaten-
Quadrupel von D und E. Dann sind und Quadrupel ihrer Pole und
. Nach der Definition des Abstands
für Punkte auf der Seite ' Orthogonalität' gilt darum:

Wenn D und E die Einheits-Kugel K nicht schneiden, sind f(d;d) und f(e;e) negativ, und der
Wert ihres hyperbolischer Winkel-Maßes ist der Betrag von .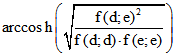
Wenn E mehrere Punkte mit K gemeinsam hat, ist f(e;e) positiv und der Wert des Winkel-
Maßes der Betrag von .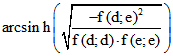
Wenn D und E die Einheits-Kugel beide in mehreren Punkten schneiden, definieren wir die
Winkel-Größe durch .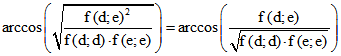

Für schneidende Geraden g und h ergibt sich daraus eine Winkel-Bestimmung, indem man sie
von den Ebenen D und E übernimmt, die g bzw. h enthalten und hyperbolisch orthogonal zu der
Ebene sind, die von g und h aufgespannt wird.

In den ersten zwölf Bildern der Gleitschau wird mit den schwarz gezeichneten Dreiecken gezeigt,
dass der Punkt Z3 in jeder der sechs Ebenen liegt, die den Innenwinkel zwischen zwei Seitenflächen
des Vierflachs ABCD halbieren. Dazu wird ABCD in verschiedenen Ansichten dargestellt, zum Teil
auch so, dass der Sehstrahl von Augenpunkt die Ebene eines der hyperbolischen Kreise euklidisch
orthogonal trifft.

Beim Vergleich der Zahlen, die zu den schwarz gezeichneten Strecken und Winkeln angegeben sind,
zeigen sich die von der euklidischen Geometrie abweichenden Regeln für die Beziehungen am
rechtwinkligen Dreieck. Die Regel wird ersetzt durch ,
die Regel durch und durch .

Das 13. und auch das letzte Bild zeigen, das nicht nur der Punkt Z3 von allen vier Ebenen-Fußpunkten
den gleichen Abstand hat, sondern auch Z0, Z1 und Z2. Das 14. bis 19. Bild zeigt die Abstände der
Punkte, die entstehen, wenn man die Ebenen-Fußpunkte um die Achsen dreht, und das 20. bis 26. Bild,
wenn man längs der Achsen verschiebt.

Das 27. bis 32. Bild zeigt die den ersten Bildern entsprechenden Maße an den schwarzen Zahlen
zu einem anderen Viereck ABCD , bei dem die Punkte Z0, Z1 und Z2 nicht so weit entfernt liegen.
Darum können auch Abstände zu Fußpunkten der Lote von Z3 auf die Achsen angezeigt werden,
die polar zu den Achsen durch Z3 sind. Es treten hier Abstände der Größe Null zwischen Punkten
auf, die zueinander polar sind, und Winkelgrößen, die mit der Länge gegenüberliegender Strecken
übereinstimmen.

Entsprechend wie in der vorangehenden Animation werden hier Ebenen-Lotfußpunkte um Achsen gedreht,
es sind dies hier aber Fußpunkte der Lote vom grünen Punkt Z1 außerhalb der Einheitskugel K auf die Seiten-
Ebenen des Vierflachs ABCD. Gedreht wird um die drei Achsen durch Z1, von denen die blaue auch durch
Z3 geht. Die grüne und die rote Achse durch Z1 ist polar zu der grünen bzw. roten Achse durch Z3 und trifft
die Einheitskugel nicht. Dieser Unterschied bewirkt, dass die entstehenden Kurven bei Drehung um diese
Achsen keine Ellipsen sind, wie bei Drehung um die blaue Achse, sondern Hyperbeln. Der Begriff 'Drehung' ist
dadurch gerechtfertigt, dass jede dieser Hyperbeln in einer Ebene liegt, die hyperbolisch orthogonal zur Achse
durch Z1 ist und deren Schnittpunkt mit der Achse von allen Hyperbel-Punkten den gleichen Abstand hat. In
dieser Ebene liegt auch die grüne bzw. rote Achse durch Z3, da sie polar zu der gleichfarbigen Achse durch
Z1 ist. Die Hyperbel-Punkte haben von dieser Achse durch Z3 alle den gleichen Abstand, entstehen also durch
Verschiebung eines Ebenen-Lotfußpunktes längs dieser Achse. Die verschiedenfarbigen Hyperbel-Hälften
treffen sich in den weiß-gefüllten Schnittpunkten der grünen und roten Achsen durch Z3 mit der Einheits-
Kugel. Die Einheits-Kugel wird in diesen Punkten von den Hyperbeln berührt.

Im zweiten Teil der Animation nach dem Aufbau der Drehungs-Spuren wird das räumliche Koordinaten-System
um 360° gedreht. Dabei wird erkennbar, dass diese Kurven auf einem einschaligen Hyperboloid liegen, das
die Einheits-Kugel berührend umschließt. Dies ist die Ex-Quadrik der Punkte außerhalb von K, die von Z1 den
gleichen Abstand haben wie die Fußpunkte der Lote von Z1 auf die Seiten-Ebenen von ABCD. Bemerkenswert
ist, dass die Fußpunkte der Lote von Z1 auf die Seiten-Ebenen von ABCD auch von Zi mit i gleich 0, 2 oder 3
jeweils gleiche Abstände haben. Ein gleiche Abstand tritt bei Punkten der Ex-Quadrik aber sonst nur auf, wenn
sie durch Drehung um die Verbindungs-Achse von Z1 und Zi entstehen.

Der dritte Teil der Animation startet mit der grünen und der gelben Ellipse, die als Spur der Drehungen um
die blaue Achse durch Z1 entstehen. Dadurch, dass zu den Drehungen Verschiebungen längs dieser Achse
nachgeschaltet werden, entstehen Kurven, deren Punkte sich als Bilder von hyperbolischen Schraubungen
ergeben, die auf die Ebenen-Lotfußpunkte angewandt werden. Diese Kuven liegen auf dem zweischaligen
Hyperboloid der Punkte außerhalb K, die von der blaue Achse durch Z1 und Z3 den gleichen Abstand
haben wie die Ebenen-Lotfußpunkte. Diese Quadrik berührt K in deren Schnitpunkten mit der blauen
Achse.

Im vierten Teil der Animation wird der Drehungs-Anteil der Schraubungen bis Null reduziert, so dass die
Hyperbeln übrig bleiben, die sich als Spur der Verschiebungen von Ebenen-Lotfußpunkten längs der
blauen Achse ergeben.

Diese sieben Bilder zeigen, dass die Ebene durch Z1 und eine Kanten-Gerade von ABCD
den Winkel zwischen den Seitenflächen durch diese Kanten halbiert.

Die Animation zeigt, dass die hyperbolischen Drehungen um eine Achse g mit den Verschiebungen längs
einer dazu polaren Achse h übereinstimmen. P sei ein Punkt, der bewegt werden soll und nicht auf g
oder h liegt. Q sei der Schnittpunkt von g mit der Ebene durch h und P. Die Gerade j durch P und Q ist
hyperbolisch orthogonal zu g und schneidet h ebenfalls orthogonal in einem Punkt R. Der hyperbolische
Abstand von Q und R ist dann (wie für alle Punkte auf g und h) die Hälfte von . Der Quotient der
Abstände PR und PQ sei tv genannt. tv ist der Betrag des Teilverhältnisses, in dem P die Strecke QR
teilt, wobei p sowohl zwischen Q und R liegen kann, als auch jenseits von Q und R.

Der Bildpunkt P' bei einer Drehung von P um g ergibt sich dann folgendermaßen: Q wird festgehalten und
R auf h in einen Punkt R' verschoben. Auf der Geraden j ist dann P' der Punkt, der die Strecke QR' im
Teilverhältnis tv teilt. Eine Verschiebung von P längs h erfolgt nach der gleichen Konstruktion.

In der Animation werden im ersten Teil Drehungen von Fußpunkten zu Loten von Z1 auf die Seitenflächen
des Vierflachs ABCD betrachtet. Dabei sind die Drehachsen die Geraden durch Z1, die gemeinsame
Lote gegenüberliegender Kanten-Geraden von ABCD sind. Sie haben die Farben magentarot, hellgrün
und hellblau. Die zugehörigen Polar-Geraden sind in der jeweils gleichen Farbe gezeichnet. Im zweiten
Teil der Animation werden die Drehungen um diese Achse durch die Verschiebungen längs dieser Achsen
ersetzt. Dies sind also die Drehungen um die zugehörigen Polar-Geraden.

Die letzten sechs Bilder der Gleitschau zeigen nach Standbildern der Animation weitere Abstände und
Winkelgrößen und ihren algebraischen Zusammenhang. Dabei werden gegenüber den oben angegebenen
hyperbolischen Fassungen von Dreiecks-Sätzen Winkelgrößen und Streckenlängen vertauscht. Es drückt
sich darin die Dualität zwischen Punkten und Ebenen dieser hyperbolischen Geometrie aus.

Zum Nachweis, dass Z3 in der Ebene liegt, die den Winkel zwischen den Seitenflächen durch AB halbiert:

Wie auf der vorigen Seite ' Kugelviereck 1' benutzen wir das Quadrupel zur Angabe der Ebene durch
die Punkte ABC. Es setzt sich aus den Vorzahlen von x, y und z und dem konstanten Glied in der Ebenen-
Gleichung zusammen. Mit bezeichnen wir das Quadrupel , das
ebenfalls die Ebene ABC beschreibt. Wir nennen es k-normiert, weil ist. Dann ist
ein Quadrupel der Ebene, die den Winkel zwischen den Seitenflächen durch AB halbiert,
denn
und .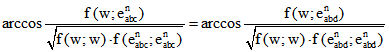
Dass auf dieser Ebene der Punkt mit dem Quadrupel
liegt, erkennt man so:
Für das innere Produkt mit w errechnet man und analog .
ist gleich
und analog gleich , folglich
.


Zur Berechnung der Schraubungs-Abbildung :

Siehe dazu Satz 32 in
'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum I'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf

Für den Drehwinkel der Schraubung benutzen wir die Bezeichnung und für die Verschiebungslänge d (in dem
oben angegebenen Satz 32 sind es und ). Die Schraubungs-Achse bestimmen wir durch ein Tripel-Paar
aus Plücker-Koordinaten s = (s ; t) mit und , aus dem auf der Seite 'Orthogonalität'
das Tripel gebildet wurde. Diese komplexe Darstellung
benutzen wir zunächst nicht. Der Bilinearform f zur Beschreibung der metrische Beziehungen von
Punkten und Ebenen entspricht bei Geraden die Bilinearform
,
zu der wir hier nur den Term der Quadratform benötigen, den wir mit fs abkürzen.
Als Bausteine zur Beschreibung der Schraubung für Ebenen-Quadrupel benutzen wir die Plücker-Matrix (nach
Julius Plücker (1801-1868))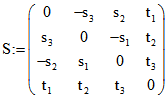
und die dazu 'polare' Matrix .
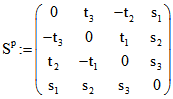sei die Matrix mit vier Zeilen und Spalten, die in der Haupt-Diagonalen nur Einsen und sonst nur Nullen hat.
Die Schraubungs-Matrix Sch für Ebenen-Quadrupel ist dann im Fall fs > 0 gleich

und im Fall fs < 0 gleich
.
Für Punkt-Quadrupel benutzt man die Matrix , die aus Sch entsteht, indem man die
inverse Matrix zu Sch an der Hauptdiagonalen spiegelt, nämlich im Fall fs > 0 die Matrix

und im Fall fs < 0 die Matrix
.
Die Verkettung von Schraubungen längs der gleichen Geraden mit den Parametern
und ist die Schraubung mit den Parametern .

Die Schraubung kann mit Hilfe des k-normierten Tripels
komplexer Zahlen und der komplexen Zahl kürzer dargestellt werden. Es gelte .
Die Matrix aus vier Zeilen und Spalten mit lauter Einsen in der Hauptdiagonalen und sonst nur Nullen sei mit
bezeichnet un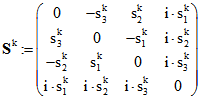d und .
sei die Matrix, die aus dadurch entsteht, dass jede Komponenten durch die dazu konjugiert
komplexen Zahl ersetzt wird. Dann wird ein Punkt-Quadrupel bei der Schraubung mit der
Winkel-Größe und der Verschiebungs-Länge d durch die Matrix abgebildet.



.