Es lebe die Geometrie!

Apollonische Kugeln beim Tetraeder

-->Pdf-Datei https://vivat-geo.de/Pdf-Dateien/Tetraeder.pdf

Unter einer apollonischen Kugel (-Fläche) zu einem Paar (A ; B) verschiedener Punkte des euklidischen
Raums und einer positiven Zahl q verstehen wir die Menge K der Punkte P, für die der Quotient der
Abstände P von B und P von A gleich q ist. Es ist also für alle P in K. R bzw. S sei der Punkt,
der die Strecke AB innen bzw. außen im Verhältnis q teilt. Das Paar (R ; S) teilt dann also das Paar (A ; B)
harmonisch mit dem Teilverhältnis q für R und -q für S. R und S sind dann Punkte von K. Aus
folgt , so dass auch das Paar (A;B) das Paar (R;S) harmonisch teilt (allerdings im Allgemeinen
mit einem anderen Verhältnis).

N bzw. T sei der Mittelpunkt von A und B bzw. R und S. Aus folgt dann
, so dass die Kugel um N durch A und B die Kugel um T durch R
und S orthogonal schneidet. Um dies zu zeigen, kann man durch A und B eine Koordinaten-Achse
legen mit 0 bei A und 1 bei B, sowie r > 0 bei R, s < 0 bei S, 0,5 bei N und bei T.
Dann ist und . Daraus errechnet man .


Für einen Punkt P außerhalb einer Kugel K ist die Potenz von P zu K das Quadrat des Abstandes PQ
eines Berührpunktes Q einer Tangente durch P an K. Da und zueinander orthogonal sind, ist
darum das Quadrat des Radius der Kugel die Potenz von N zu und das Quadrat des Radius
der Kugel die Potenz von T zu .

Wir betrachten auf dieser Seite sechs apollonische Kugeln zu einem Tetraeder ABCD, deren Beziehung
zueinander durch einen Raumpunkt X festgelegt wird, von dem nur verlangt wird, dass er auf keiner
Seiten-Ebene von ABCD liegt. Jede dieser Kugeln hat den Mittelpunkt auf einer Kanten-Gerade von
ABCD und schneidet diese in Punkten R und S, so dass das Paar der Eck-Punkte darauf, z. B. (A ; B),
harmonisch geteilt wird. Die Teilungs-Punkte im Innern von gegenüberliegenden Kanten sind dabei kollinear
mit X. Diese Teilungs-Punkte sind durch X für ABCD eindeutig bestimmt, da jede Ebene durch X und eine
Kante einen eindeutigen Schnittpunkt mit deren Gegen-Kante hat. Wir nennen diese Teilungs-Punkte
'Spur-Punkte von X auf den Kanten von ABCD' und X 'Testpunkt'.

Analog wie die sechs apollinischen Kugeln zu einem Testpunkt X bei ABCD kann man drei apollinische Kreise
zu einem Testpunkt X bei einem Dreieck definieren. Besonderes Interesse erlangte dabei das Inkreis-Zentrum
X des Dreiecks. Denn dafür schneiden sich die drei apollonischen Kreise in den beiden isodynamischen Punkten
des Dreiecks, deren Lot-Fußpunkte auf den Seiten-Geraden stets ein gleichseitiges Dreieck bilden. Leider ist
über die besonderen geometrischen Eigenschaften von Schnittpunkten der sechs apollinischen Kugeln zu
Testpunkten bei Tetraedern wenig bekannt. Immerhin kommt es vor, dass alle sechs Kugel-Flächen zwei
gemeinsame Punkte haben. Die Zusammenhänge zwischen den sechs Kugeln sollen in den folgenden
Animationen dargestellt werden.

Die apollonischen Kreise wurden nach dem antiken Mathematiker Apollonius (-265 bis -190) benannt.

Das erste Bild dieser Animation zeigt den weitgehend zufällig gewählten umrandeten schwarzen Punkt X
mit seinen Spur-Punkten auf den Kanten AB, BD und DA. Diese wurden mit dem Schnittpunkt
der Geraden XC mit der Gegen-Seite ABD zu C konstruiert, indem z. B. die Gerade mit der
Geraden AB geschnitten wurde. Diesen Spur-Punkt von X auf der Kante AB bezeichnen wir mit
. Wenn X das baryzentrischen Koordinaten-Quadrupel hat, dann hat
das Quadrupel und das Quadrupel . Der blaue Kreis durch
ist der apollonische Kreis zu (A ; B) im Dreieck ABD zum Teilverhältnis . Sein Mittelpunkt
hat das unnormierte Quadrupel mit den Quadraten von und . Daraus entsteht
das zugehörige normierte Quadrupel durch
Anwendung der Normierungs-Funktion N, bei der durch die Summe der Komponenten geteilt wird.

Die zu den drei Spur-Punkten von X auf dem Dreieck ABD gehörigen zweiten Schnittpunkte mit den
Kanten-Geraden mit den Quadrupeln , und
liegen auf einer Geraden, die ' trilineare Polare von ' genannt wird. Die Determinate der Matrix
aus den drei Tripeln, die aus den Quadrupeln durch Streichung der dritten Komponente entsteht, hat
nämlich den Wert Null. Entsprechend zeigt man, dass die Zentren der apollonische Kreise zu (A ; B) ,
( D ; A ) und ( D ; B ) kollinear sind.

Die nach dem ersten Bild gezeigte Bewegung eines Punktes P auf dem Kreis verdeutlicht, dass der Quotient
der Abstände zu A und zu B konstant bleibt. Das Gleiche gilt für einen weiteren Kreis auf der anschließend
grau gezeichneten apollonischen Kugel zu (A ; B) zum gleichen Teilverhältnis. Dieser Vorgang wird für die
entsprechenden Kugelln zu ( D ; A ) und ( D ; B ) wiederholt.

Das anschließende Standbild zeigt, dass sich die drei apollonischen Kreise in zwei Punkten schneiden, die
kollinear mit dem Zentrum des Umkreises von ABD sind. Dieser Umkreis ist orthogonal zu jedem der
drei Kreise. Denn nach der Berechnung oben auf dieser Seite ist für den Mittelpunkt N von AB und die
Potenz zum Apollonius-Kreis zu (A ; B) gleich dem Quadrat des Radius vom Thales-
Kreis über AB. Wenn man in der Gleichung auf beiden Seiten addiert,
ergibt sich links die Potenz von zum Apollonius-Kreis und rechts das Quadrat vom Radius
des Umkreises von ABD , da das Dreieck rechtwinklig ist. Dann ist aber auch die Potenz von
zum Apollonius-Kreis zu (A ; B) das Quadrat des Radius vom Umkreis und damit gleich dem Quadrat des
Abstands des Berührpunktes Q einer Tangente von an den Apollonius-Kreis. Die analoge
Überlegung zu den Apollonius-Kreisen zu (A ; D) und (D ; B) zeigt, dass die Potenz von zu allen drei
Kreisen gleich ist und dies für alle Punkte der Lotgeraden g zur Verbindungs-Geraden zweier Kreis-Zentren
gilt. Die drei Zentren müssen darum kollinear sein, und g Potenz-Gerade zu allen drei Kreisen. Dies bedeutet
aber nicht, dass sich die drei Kreise stets gemeinsame Schnittpunkte haben, wie die folgende Animation klar macht.

Die drei apollonischen Kreise werden in der letzten Phase der Animation zu den den passenden apollonischen
Kugeln ergänzt, die sich in einem Kreis schneiden.

Das erste Bild der Animation zeigt die Spurpunkte von X auf den Kanten der Seiten-Dreiecke ABD und
BCD . Sie werden im zweiten Bild um die Punkte der zugehörigen trilinearen Polaren ergänzt. Nach
einer 360°-Drehung wird die Zeichnung auf die Punkte von BCD reduziert und dann wie in der vorigen
Animation zu den apollonischen Kugeln erweitert. Dabei zeigt sich, dass die Lotgerade vom Umkreis-
Zentrum von BCD auf die Verbindungs-Gerade der drei Kugel-Zentren auch hier Potenz-Gerade der
drei Kreise und auch der drei Kugeln ist, aber die Kugeln keine gemeinsamen Punkte haben.

Das ersten beiden Bilder der Animation stellen die -Punkt-Geraden-Konfiguration wie auf den
Seiten ' Kugelviereck 1' und ' Symmetrie' dar. Das dritte Bild zeigt, dass die Ergänzung dieser Konfiguration
um die Kanten-Geraden des Tetraeders ABCD die gleiche Figur ergeben, wie die Spur-Punkte von X auf
den vier Seiten-Dreiecken mit ihrer Ergänzung um die trilinearen Polaren und die Kanten-Geraden. Im
vierten Bild werden die Mittelpunkte der apollonischen Kreise zu allen sechs Kanten von ABCD zugefügt,
zusammen mit den Verbindungen von je dreien. Auf Grund der Kollinearität von je drei Zentren folgt, dass
alle sechs Mittelpunkte in einer Ebene liegen, die auch 'Lemoine-Ebene zu X' genannt wird, zu Ehren von
Emile Lemoine (1840 bis 1912). Ihr baryzentrisches Quadupel ist .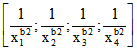

Die Konfiguration wird dann so gedreht, dass die Lemoine-Ebene parallel zur Bildschirm-Ebene liegt.

Die anschließenden 12 Standbilder zeigen für jede der vier Seiten-Dreiecke die apollonischen Kreise, die
zugehörigen Kugeln und die Schnitt-Kreise dieser Kugeln mit der Lemoine-Ebene. Alle sechs Schnitt-Kreise
mit der Lemoine-Ebene sind orthogonal zu dem Schnitt-Kreis dieser Ebene mit der Umkugel von ABCD .
In der letzten Phase der Animation zeigt eine geeignete Drehung, dass der Fußpunkt des Lots vom
Umkugel-Zentrum auf die Lemoine-Ebene der Schnittpunkt der vier Potenz-Geraden zu den jeweils drei
Schnitt-Kreisen ist, die zu den Seiten-Dreiecken von ABCD gehören.

Diese Gleitschau soll zeigen, dass sich aus den Spurpunkten des Testpunktes X und den zugehörigen
trilinearen Polaren noch weitere Schnittpunkte ergeben, die für die apollonischen Kugeln bedeutsam
sind. Das erste Bild zeigt den schwarzen Test-Punkt X mit den farbigen Spurpunkten auf den Kanten-
Geraden von ABCD . Die farbigen Strecken gehören zu den trilinearen Polaren in den Ebenen der
Seiten von ABCD . Die sechs farbigen Punkte darauf ergänzen die Spurpunkte auf den Kanten zu
Paaren, welche die Kanten harmonisch teilen. Die weiß gefüllten Punkte sind die Zentren der
apollonischen Kugeln in der Lemoine-Ebene von X. Die grauen Verbindungs-Geraden der farbigen
Punkte haben jeweils zu dritt sieben weitere gemeinsame Punkte. Die Drehung der Figur verdeutlicht
dies.

Im zweiten Standbild werden die sieben Punkte markiert. Im nächsten Bild werden drei der sieben
Punkte mit X zu dem Tetraeder AgBgCgDg durch hellblauen Kanten verbunden und die übrigen
vier mit hellgelben Kanten zu dem Tetraeder AuBuCuDu . Die Buchstaben g und u stehen dabei für
'gerade' und 'ungerade', denn dies kennzeichnet die Anzahl der Vorzeichen in den baryzentrischen
Quadrupeln dieser Punkte. Wenn X = Dg das baryzentrische Quadrupel hat,
ergibt sich für Ag, Bg und Cg , und und
für Au, Bu, Cu und Du , , und
(Au, Bu , Cu sind hier leider permutiert).

Die 18 Kanten-Geraden der Tetraeder ABC D , Au Bu Cu Du und Ag Bg Cg Dg bilden mit ihren
12 Eck-Punkten, den 6 Spur-Punkten von X auf den Kanten von ABC D und deren 6 harmonisch
konjugierten Punkten auf den trilinearen Polaren eine -Punkt-Geraden-Konfiguration, bei
der die 4 Punkte einer Geraden unterschiedliche Farben haben. Die vier Punkte einer Geraden trennen
sich paarweise, wobei jedes Paar das andere innen und außen im gleichen Verhältnis teilt.

Da für das Zentrum und den Radius der apollonischen Kugeln zu einem Test-Punkt X nur die Quadrate
der baryzentrischen Koordinaten von X benutzt werden, bleiben sie unverändert, wenn man X durch
irgendeinen der Eckpunkte von AgBgCgDg oder AuBuCuDu ersetzt.

Im vierten und fünften Standbild werden die zwölf Eckpunkte der drei Teraeder ABCD , AgBgCgDg
und AuBuCuDu durch farbige Geraden verbunden, die erkennbar machen, dass auch hier eine
-Punkt-Geraden-Konfiguration ersteht wie in der vorangehenden Animation. Dort sind
die zwölf Eckpunkte die Schnittpunkte der Kanten-Geraden von ABCD mit den apollonischen
Kugeln, welche die Kanten von ABCD harmonisch teilen. Nach der Drehung werden die beiden
Konfigurationen zusammen gezeigt.

In den folgenden beiden Animationen werden die Tetraeder AgBgCgDg und AuBuCuDu für das
Inkugel-Zentrum X betrachtet. Die Eckpunkte sind dann alle Zentren von Kugeln, die alle vier
Seiten-Ebenen von ABCD berühren.

Das erste Bild verdeutlicht, wie sich die Eckpunkte von AgBgCgDg aus X ergeben. Jeder der drei Punkte
Ag, Bg und Cg teilt zusammen mit X die Spur-Punkte von X auf gegenüber liegenden Kanten von ABCD
harmonisch. Um die im folgenden Bild zugefügten Kugeln als Berühr-Kugeln der Seiten-Ebenen von
ABCD erkennbar zu machen, werden für zwei dieser Ebenen die Berührpunkte durch kleine Dreiecke
markiert und anschließend der Augenpunkt auf eine Kanten-Gerade von ABCD verschoben, so dass
die Bild-Ebene der Projektion orthogonal zu dieser Geraden ist. Dies wird für alle sechs Kanten-Geraden
wiederholt. In diesen Projektionen erkennt man die Lage der Kugeln in Bezug auf das Paar zweier Seiten-
Ebenen, das wir 'Kanten-Dieder' nennen. Unter dem Inneren eines Kanten-Dieders verstehen wir die
Vereinigungs-Menge aller Ebenen durch die zugehörige Kante, welche Punkte von ABCD treffen. Es
zeigt sich, dass bei jedem Kanten-Dieder genau zwei der Kugeln im Innern liegen.

Das erste Bild zeigt, wie sich das Tetraeder AuBuCuDu aus dem Test-Punkt X ergibt. Jeder farbige
Spurpunkt P auf einer Kante K von ABCD ist durch graue Verbindung ein Punkt P' zugeordnet, der
zusammen mit P die Kante harmonisch teilt. P ist mit dem Punkt Q' gelb verbunden, der zu dem
Spur-Punkt Q auf der gegenüberliegenden Kante von K gehört. Die Geraden zu den vier gelben
Strecken schneiden sich in den Eckpunkten von AuBuCuDu .

Die Verschiebungen des Augenpunktes zeigen, dass jede der vier Berühr-Kugeln mit einem Eck-Punkt
von AuBuCuDu genau eine der Seiten-Ebenen von ABCD von außen berührt, also in dem Halb-Raum
dieser Seite-Ebene liegt, der ABCD nicht anthält.

Lotfußpunkte und Abstände in baryzentrischen Koordinaten beim Tetraeder

Zur Berechnung der Lotfußpunkte und Abstände in baryzentrischen Koordinaten benutzen wir die
Komponenten der am Schluss der Seite ' Monge' eingeführten Maß-Matrix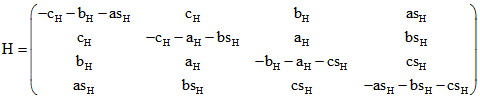
.
Diese sind die Skalarprodukte von Vektoren, die euklidischen orthogonal zu den Seiten-Ebenen von ABCD
stehen und deren Länge gleich dem Kehrwert vom Abstand des gegenüberliegenden Eckpunktes ist. Die
Zahl bzw. ist das Skalarprodukt von Vektoren zu Seiten-Flächen, die sich in
der Kante mit der Länge as , bs , cs, a , b bzw. c treffen. In der Haupt-Diagonalen stehen die Quadrate der
Längen dieser Vektoren, also die Quadrate der Kehrwerte von den Längen der Raum-Höhen. Wir kürzen ab:
, , , .
Das Volumen V von ABCD beträgt ein Drittel des Produkt aus dem Inhalt einer Seiten-Fläche und der
zugehörigen Höhe. Darum ist das Quadrupel der Inhalte der
Seitenflächen BCD , ACD , ABD und ABC.

Die normierten baryzentrische Koordinaten eines Testpunktes X ergeben sich, indem
man die Volumen der Tetraeder XBCD , AXCD , ABXD und ABCX durch das Volumen von ABCD
teilt und das Ergebnis eventuell mit einem Minus-Zeichen versieht. Das Minus-Zeichen ist zum Beispiel bei
der ersten Komponente nötig, wenn die Seiten-Ebene von BCD zwischen A und X verläuft. Unter dem
'signierten Abstand' des Punktes X von der Seiten-Ebene von BCD verstehen wir dann das Produkt der
Entfernung X vom Lotfußpunkt auf der Seiten-Ebene von BCD mit -1. Entsprechendes gilt für die anderen
Komponenten.

Da die Tetraeder XBCD und ABCD die Grundfläche BCD gemeinsam haben, stimmt der Quotient der
Volumen mit dem Quotient der Abstände der Punkt X und A von der Seiten-Ebene BCD überein. Der
signierte Abstand X von BCD ist also das Produkt von und dem Abstand des Punktes A von BCD .
Darum ist 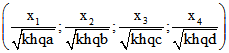das Quadrupel der signierten Abstände des Punktes X
von den Seiten-Ebenen zu BCD , ACD , ABD und ABC.

N sei die Funktion, die jedem baryzentrischen Quadrupel das zugehörige normierte Quadrupel
zuordnet, indem man durch die Summe der Komponenten teilt. Wenn X ein Berühr-Kugel-
Zentrum von ABCD ist, gilt . Dann sind alle
Abstände des Punktes X von den Seiten-Ebenen zu BCD , ACD , ABD und ABC gleich dem
Betrag von . Für eine Zahl z sei sign(z) gleich 1 bzw. 0
bzw. -1, wenn z positv bzw. Null bzw. negativ ist. Dann ist das Quadupel der signierten Abstände
von X zu den Seiten-Ebenen von BCD , ACD , ABD und ABC gleich .

Die Fußpunkte der Lote von einem beliebigen Punkt X auf die Seiten-Ebenen zu BCD , ACD , ABD
und ABC ergeben sich als Schnittpunkte dieser Ebenen mit den Geraden durch X und den unendlich
fernen Punkten, deren Quadrupel durch die Zeilen von der Matrix H gegeben sind. Es ergeben sich
die Punkte