Es lebe die Geometrie!

Konstruktion einer Penrose-Kachelungen
mit einem 5-Gitter nach de Bruijn

N.G. de Bruijn hat in dem Zeitschriften-Artikel
'Algebraic Theory of Penrose's Non-periodic Tilings of the Plane'
(Verhandlingen der Koninklijke Nederlandse Akademie van Wetenschaften 1981/A84)
ein Verfahren zur Konstruktion von Penrose-Kachelungen mit Hilfe eines 5-Gitters (Pentagrid) dargestellt.
Dabei geht man von rellen Zahlen mit der Summe Null aus. Diese Zahlen geben den
signierten Abstand der Urspungs von fünf Geraden an, deren Normalenvektor mit
der Rechts-Achse den Winkel 0°, 72°, 144°, 216° bzw. 288° einschließt.
für ist der Vektor mit der Länge 1 und dem Richtungswinkel . Die Geraden
haben die Gleichung oder bei Verwendung des
inneren Produkts. Der Term gibt für einen beliebigen Punkt (x;y) den signierten Abstand von
an.

mit ganzzahligem j sei die Gerade mit der Gleichung . Sie ist parallel zu und hat
den signierten Abstand von . Die Menge der Geraden für ganze Zahlen j und
wird als 5-Gitter oder als Pentagrid bezeichnet. Wir setzen immer voraus, dass im Pentagrid nie drei
Geraden einen gemeinsamen Schnittpunkt haben. Das Pentagrid bezeichnen wir auch als 'D-Pentagrid',
wenn mit D das 5-Tupel gemeint ist.

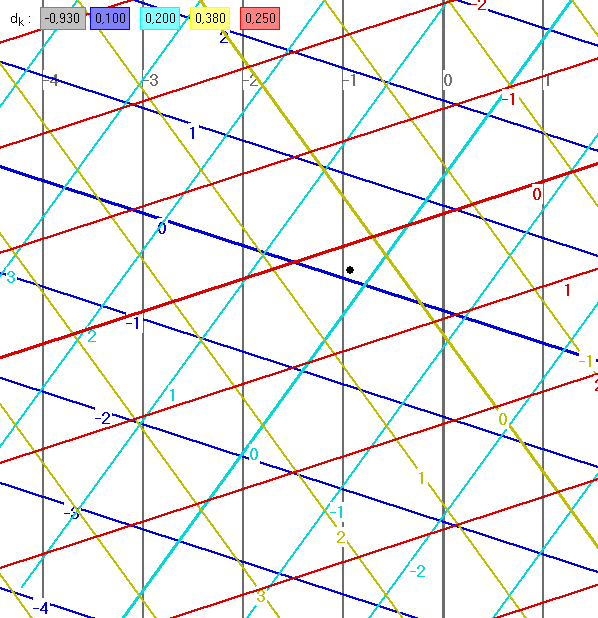
Die folgende Gleitschau zeigt Beispiele dazu. Dabei sind die Geraden grau gezeichnet, dunkelblau,
hellbau, gelb-grau und rot. Die Kachelung des Pentagrids nennen wir 'de Bruijn-Kachelung'.
Die (zum Teil sehr kleinen) Kacheln werden ebenfalls in den Farben dunkelblau, hellblau, gelb und rot
dargestellt, nach einem Prinzip, das unten erklärt wird. Im Widerspruch zum Augenschein gehen keine
drei Geraden der Pentagrids durch einen gemeinsamen Schnittpunkt. Der schwarze Punkt in der Mitte
ist der Koordinatenursprung (0 ; 0).

Die besonderen Eigenschaften des Pentagrids beruhen darauf, dass die Summe der fünf Vektoren gleich
Null ist. Daraus folgt für einen beliebigen Punkt (x ; y) der Ebene, dass die Summe seiner signierten Abstände
von den fünf Geraden gleich , also
wegen ebenfalls Null ist. Wenn man hierbei jede der Geraden durch eine
Parallele im Pentagrid ersetzt, ist die Abstandssumme für alle Punkte (x : y) eine konstante ganze Zahl.
Zum Beispiel ergibt sich für die Abstandsumme .

Die Färbung der Kacheln in der de Bruijn-Kachelung kommt nun folgendermaßen zustande:
P sei irgendein Punkt der Ebene. Zu jedem gibt es genau ein ganzzahliges j, so dass der
signierte Abstand des Punktes P von größer als -1 und kleinergleich Null ist. ist
also die Gerade des Pentagrids, die in der Richtung zum Winkel dem Punkt P am nächsten liegt.
Wir bezeichnen diese ganze Zahl j mit j(k ; P), die zugehörige Gerade mit g(k ; P). Da die Summe der
für gleich Null ist und dies auch für die gilt, ist die Summe der signierten Abstände
zu den fünf Geraden g(k ; P) gleich . Wegen
ist dies eine der Zahlen -4 , -3 , -2 , -1 , nicht aber Null, da sonst alle fünf
Geraden g(k ; P) durch P gehen würden. Wir nennen nach
de Bruijn 'Index von P' und kürzen mit ind(P) ab. Ind(P) ist also stets eine der Zahlen 1 , 2 , 3 oder 4.
Alle Punkte einer Kachel der de Bruijn-Kachelung haben den gleichen Index. Wenn wir der '1' die Farbe
dunkelblau zuordnen, der '2' hellblau, der '3' gelb und der '4' rot, ergibt sich so die Färbung der Kacheln.
Kacheln mit einer gemeinsamen Seite haben Indizes, die sich um 1 unterscheiden. Da die ganzen Zahlen
j(k ; P) für alle Punkt der gleichen Kachel K übereinstimmen, bezeichnen wir sie auch durch j(k ; K).

Bei einer Kachel K vom Index 1 sind alle Seitengeraden Gitter-Geraden mit j = j(k ; K), während
bei einer Kachel vom Index 4 alle Seitengeraden Gitter-Geraden mit sind. Als
'Frontgerade von K' bezeichnen wir aus diesem Grund bei einer Kachel K vom Index 1 bzw. 4 jede
der fünf Geraden mit bzw. , auch für Werte von k, für die diese Geraden
keine Seiten-Geraden sind. Für Kacheln vom Index 1 und 4 sind die gleichen Formen möglich. Auch
die Kacheln vom Index 2 und 3 haben die gleichen möglichen Formen. Alle Sätze über de Bruijn-
Kachelungen bleiben wahr, wenn man 'Index 1' durch 'Index 4' ersetzt und 'Index 2' durch 'Index 3'.
Darum nennen wir 'Frontgerade' auch bei einer Kachel K vom Index 2 bzw. 3 jede der fünf Geraden
mit bzw. .

Jeder Kachel K der de Bruijn-Kachelung wird der Punkt Pen(K) der Ebene zugeordnet, dessen
Ortsvektor ist. Dabei bezeichnen
wir diesen Ortsvektor ebenfalls mit Pen(K). Es zeigt sich, dass die Menge der Punkte Pen(K) für
Kacheln K mit dem Index 2 oder 3 die Eckpunktmenge von Boot-, Kronen- und Stern-Kacheln einer
Penrose-Kachelung sind, deren Zentren durch die Punkte Pen(K) mit Kacheln K vom Index 1 oder 4
bestimmt werden. Die Seiten der Boot-, Kronen- und Stern-Kacheln ergeben sich bei der Abbildung Pen
durch die Verbindungsstrecke der Bilder Pen(K1) und Pen(K2) von Kacheln K1 und K2 vom Index
2 und 3 mit einer gemeinsamen Seite. Wenn eine Kachel K1 vom Index 1 bzw. 4 eine gemeinsame
Seite mit einer Kachel K2 vom Index 2 bzw. 3 hat, ist die Verbindungsstrecke von Pen(K1) und
Pen(K2) Seite eine der Rauten, mit der sich eine Boot-, Kronen- oder Stern-Kachel zusammensetzen
lässt. Siehe dazu die folgenden Animationen.

In dieser Animation bewegt sich ein Punkt P auf einem spiralförmigen Weg aus dem Ursprung des
Koordinatensystems einer de Bruijn-Kachelung. Die Kacheln, die P dabei trifft, werden nacheinander
farbig markiert. Das Gleiche geschieht mit den von P getroffenen 5-Gitter-Geraden. Von P aus zeigt der
linke weiß gefüllte Pfeile auf den Punkt Pen(P) der zugehörigen Penrose-Kachelung, die hier in einem
getrennten Koordinatensystem gezeigt wird, in dem alle Verbindungsstrecken die Länge 1 haben. Jede
neue Verbindungsstrecke ist senkrecht zu der Gitter-Geraden gerichtet, die P gerade kreuzt. Sie hat
darum die gleiche Farbe wie die Gitter-Gerade.

Der rechte weiß gefüllte Pfeil zeigt auf einen Punkt Pen2(P) in einem dritten Koordinatensystem mit
dreimal so großer Einheitslänge wie bei der Penrose-Kachelung. Pen2(P) wird analog wie Pen(P)
definiert, allerdings mit einer geänderten Zuordnung der Vektoren , wie folgende Gegenüberstellung
zeigt:




Die Richtungswinkel sind bei der Abbildung Pen2 also gegenüber denen bei Pen verdoppelt. Denn zum
Beispiel hat den Richtungswinkel . Während sich die Punkte Pen(K)
in einer unregelmäßigen Spiralbewegung vom Ursprung entfernen, gilt dies nicht für die Punkte Pen2(K).
Diese bleiben stets im Innern der Vereinigungsmenge des hellblau und des gelb berandeten Fünfecks. Die
Verbindungsstrecken bei den Bildern von Pen2 kreuzen sich zum Teil, was bei der Abbildung Pen nie
vorkommt.

Die Kachel-Seiten der de Bruijn-Kachelung wurden hier mit einer dunkelblauen oder roten Markierung
versehen, die angibt, ob beim Kreuzen der Seite zwischen einer Kachel K1 und einer Nachbar-Kachel
K2 der Index wächst oder abnimmt. (Wenn Eckpunkte einer Kachel sehr nahe beieinander liegen, wird
auf diese Seiten-Markierung verzichtet.) Wir benutzen die Bezeichnung 'Plus-Seite' bzw. 'Minus-Seite'.
Im ersten Fall gelangt man von Pen(K1) zu Pen(K2) durch Ansetzen des Vektors , der senkrecht zur
Seitengeraden steht, im zweiten Fall muss man stattdessen den Gegenvektor ansetzen. Dies zeigt die
Gleitschau nach der Animation mit Standbildern daraus. Denn nach jedem Standbild wird die Vektor-
Kette gezeigt, die den Koordinatenursprung der Penrose-Kachelung mit dem jeweils letzten Punkt
Pen(K) verbindet.

Diese Animation zeigt das Anlegen der Boot-, Kronen- und Stern-Kacheln in der Penrose-Kachelung
durch Umrunden der Kacheln vom Index 1 oder 4 in der de Bruijn-Kachelung. Die farbig unterlegten
ganzen Zahlen zwischen 0 und 9 geben die Richtungs-Zahlen k an, die den Richtungswinkeln
beim Kreuzen einer Gitter-Geraden zugeordnet sind. An Stelle der Vielfachen von 72° werden hier
Vielfache von 36° benutzt, weil bein Übergang zu einer Kachel mit kleinerem Index die Richtung der
Bewegung gegen einen der Vektoren erfolgt. Zum Beispiel ist der Gegenrichtungswinkel zu
der Richtungswinkel . Die weiß unterlegten ganzen
Zahlen am oberen Rand sind die Differenzen der darüber stehenden Richtungszahlen modulo 10. Die
Folge dieser Zahlen charkterisiert die Form einer Boot-, Kronen- und Stern-Kachel. Sie ist für die
Boot-Kachel 113113, für die Kronen-Kachel 93931113 und für die Stern-Kachel 9393939393
oder eine Ziffern-Folge, die daraus durch zyklische Verschiebung entsteht.

Gegenüber der vorherigen Animation wird beim Umrunden der Kacheln vom Index 1 oder 4 an jeder
ihrer Seiten ein Abstecher ins Innere der Kachel gemacht. Für die Penrose-Kacheln bedeutet dies
den Aufbau der Boot-, Kronen- bzw. Stern-Kachel aus 3, 4 bzw. 5 Rauten mit einem Innenwinkel
72° oder 144°.

Der Zusammenhang zwischen der Form der Boot-, Kronen- bzw. Stern-Kacheln und der Form
der umrundeten Kacheln vom Index 1 oder 4 kann folgendermaßen analysiert werden:

Man denke sich zu jeder Seite einer de Bruijn-Kachel einen dazu senkrecht nach außen gerichteten
Vektor der Länge 1. Wir nennen ihn 'Außen-Vektor'. Die Summe aus dem Winkel zwischen zwei
benachbarten Außen-Vektoren und dem Innenwinkel zwischen den zugehörigen Seiten ist stets 180°.
Die Summe aller Winkel zwischen benachbarten Außen-Vektoren beträgt 360°. Die Summe der
zugehörigen Richtungszahl-Differenzen ist also 10. Für die Kacheln vom Index 1 oder 4 sind diese
Richtungszahl-Differenzen alle gerade, da die Richtugszahlen selbst alle gerade bzw. ungerade sind.
Bei allen de Bruijn-Kacheln sind alle Winkel zwischen benachbarten Außen-Vektoren kleiner als 180°,
so dass als Richtungszahl-Differenzen nur die Zahlen 1, 2, 3 und 4 in Frage kommen, beim Index 1
oder 4 also 2 und 4. Es gibt nur drei Möglichkeiten, die Zahl 10 als Summe mit den Zahlen 2 und 4
darzustellen, nämlich 10 = 4 + 4 + 2 = 4 + 2 + 2 + 2 = 2 + 2 + 2 + 2 + 2. Die zugehörigen
Kombinationen von Innenwinkeln sind also 36° + 36° + 108° beim Dreieck, 36° + 108° + 108° + 108°
beim Viereck und 108° + 108° + 108° + 108° beim Fünfeck.

An jede Kreuzung zweier Gitter-Geraden g und h an einer Ecke einer de Bruijn-Kachel treffen vier
Kacheln aufeinander. K0 sei eine Kachel davon mit minimalem Index imin. Die Seiten von K0,
die auf g und h liegen, sind Plus-Seiten, bei ihnen wächst also der Index beim Übergang zur
Nachbar-Kachel. In einem Rundweg um den Eckpunkt beginnend bei K0 über g ergibt sich für
die Kachel K1 der Index imin+1, dann für K2 der Index imin+2, da K1 und K2 auf der gleichen
Seite von h liegen, dann für K3 der Index imin+1 nach Kreuzung von g an einer Minus-Seite von
K3 und schließlich wieder imin nach Kreuzung von h an einer Minus-Seite von K3. K1 und K3
haben also den gleichen Index, und die Indizes von K0 und K2 unterscheiden sich um 2. Für die
zugehörige Figur in der Penrose-Kachelung ergibt sich eine Raute, da g und h je zweimal gekreuzt
werden. Darum treffen in allen Punkten Pen(K) für Kacheln K vom Index 1 oder 4 Rauten
zusammen, deren Anzahl mit der Anzahl der Eckpunkte von K übereinstimmt. Auf Grund der
möglichen Kombinationen der Richtungszahl-Differenzen sind hierbei die Innenwinkel bei Pen(K)
im Fall eines Dreiecks K 144° , 144° , 72°, im Fall eines Viereck 144°, 72°, 72°, 72° und im Fall
eines Fünfecks 72°, 72° 72°, 72°, 72° . Auf diese Weise entsteht notwendig eine Boot-, Kronen-
bzw. Stern-Kachel.

Das erste Bild der sechs Bilder der Gleitschau zeigt eine mit einem Pentagrid konstruierte Penrose-
Kachelung in einer Darstellung mit Rauten und Seiten-Pfeilen und die zugehörigen Pen2-Bilder.
Im zweiten Bild wurden nur die Punkte zum Index 2 und 3 gezeichnet. Die Pfeile ergeben sich nach
folgendem Prinzip:

Jede Rauten-Seiten mit einem Endpunkt vom Index 1 oder 4 hat die Pfeilspitze bei diesem Endpunkt.
Die dazu parallele Seite ist bei einer 72-Raute gleichgerichtet, bei einer 144°-Raute entgegengerichtet.

Nach dieser Regel erhält man Boot- Kronen- und Stern-Kacheln mit Seiten-Pfeilen, die nur aperiodische
Kachelungen zulassen. Offenbar ergibt sich die Seitenorientierung nicht unmittelbar aus den Indizes der
de Bruijn-Kacheln. Man kann aber in folgender Weise eine andere dafür geeignete Kennzahl ecko
definieren: Für Kacheln K vom Index 1 oder 4 sei ecko(K) gleich Null, für K vom Index 2 bzw. 3 die
Anzahl der Plus- bzw. Minus-Seiten von K. Dies ist in der zugehörigen Penrose-Kachelung die Anzahl
der Seiten von Boot-, Kronen- und Stern-Kacheln, die in Pen(K) zusammentreffen. Wenn K1 und K2
eine Seite gemeinsam haben, zeigt der Seiten-Pfeil genau dann von Pen(K1) nach Pen(K2), wenn
ecko(K2) kleiner als ecko(K1) ist.

In den letzten vier Bildern der Gleitschau werden nur Kacheln mit gleichem Index gezeichnet, zusammen
mit ihren Pen2-Bildpunkten. Zu jedem Index gehört ein reguläres Fünfeck, in dessen Innern alle Bildpunkte
mit diesem Index liegen. Eine Begründung hierfür findet man am Schluss dieser Seite.

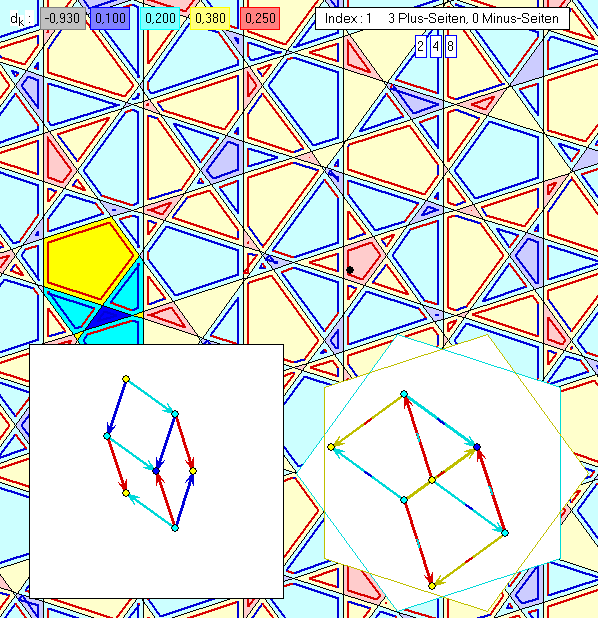
Diese Gleitschau zeigt Kachel-Komplexe mit einer Zentrums-Kachel und weiteren Kacheln, die sie in
mindestens einem Punkt berühren, zusammen mit den zugehörigen Pen- und Pen2-Bildern. Bei den
Pen2-Bildern wurden die Verbindungs-Pfeile nicht nur in der Farbe gezeichnet, die zu ihrer Richtung
gehört, sondern im mittleren Teil auch in der Farbe, die bei dem Pfeil zwischen den zugeordneten
Pen-Bildern benutzt wird. Das Pen-Bild der Zentrums-Kachel wurde stets in die Mitte des Quadrats
verschoben, beim Pen2-Bild gab es eine derartige Korrektur nicht.

Die Pen2-Bilder haben mit den Pen-Bildern gemeinsam, dass sie sich aus 72°- und 144°-Rauten
zusammensetzen. Dem Anlegen einer 72°-Raute bei den Pen-Bildern entspricht das Anlegen einer
144°-Raute bei den Pen2-Bildern, und umgekehrt. Während dies bei den Pen-Bildern ohne
Überlappung der Rauten geht, ist es bei den Pen2-Bildern nicht möglich. Wir bezeichnen darum das
Ergebnis des Anlege-Prozesses bei den Pen2-Bildern als Pen2-"Kachelung" in Anführungsstrichen.


Begründung für den Zusammenhang zwischen der nach de Bruijn konstruierten
Penrose-Kachelung und der Pen2-"Kachelung":

Zu jedem Index gehört ein reguläres Fünfeck, in dessen Innern alle Pen2-Bildpunkte mit diesem Index
liegen. Der Vektor ist Ortsvektor des Mittelpunkts der
Fünfecke. sei das Fünfeck (einschließlich des Inneren), das die Vektoren als Eckpunkt-Vektoren
hat. sei das Fünfeck mit den Eckpunkt-Vektoren , wobei wir mit
identifizieren. und entstehen aus bzw. durch Punktspiegelung am Mittelpunkt.
Dann liegen die Pen2-Bildpunkten zum Index ind alle im Innern des Fünfecks .
(Dabei haben wir Ortsvektoren und zugehörige Punkte identifiziert.)

Zunächst soll das Innere der Fünfecke charakterisiert werden.
Es gilt der folgende

Satz 1: p ist der Ortsvektor eines Punktes im Innern von genau dann, wenn es reelle Zahlen
gibt mit und ,
die alle größer als Null und kleiner als 1 sind.
Beweis: : p sei zunächst als Ortsvektor eines Punktes im Innern von vorausgesetzt. Dann liegt
der Punkt im Innern einer Strecke AD, wobei A ein Eckpunkt von ist und D auf der Verbindung
der beiden A gegenüber liegenden Eckpunkten B und C liegt. Für die zugehörigen Ortsvektoren
a, b, c, d gilt dann :
Es gibt mit mit , und und es gibt
mit , und .

1.Fall: ind = 1. Dann ist und für die Vorzahlen gilt:
und .

2.Fall: ind = 2. Dann sind a, b, c die Summen zweier benachbarter Vektoren aus ,
wobei die Summanden von A nicht unter denen von B und C vorkommen, z. B.
, und . Dann ist

mit und .

3. bzw. 4. Fall: ind = 3 bzw. ind = 4. Aus folgt dann . Nach dem geraden Bewiesenen
gibt es dann mit der Summe und .
Wegen folgt
mit Vorzahlen zwischen 0 und 1 und der Summe .

"": Es sei nun vorausgesetzt, dass es positive reelle Zahlen kleiner als 1 gibt mit und . Zu zeigen ist dann .

1. Fall: ind =1 : Wegen der Symmetrie des Fünfecks reicht es zu zeigen, dass der x-Wert von p größer als
der x-Wert cos(144°) der Eckpunkte zu und ist. Da die x-Werte von positiv sind, ist nur
zu zeigen, dass der x-Wert von größer als cos(144°) ist. Das ist aber
wahr, weil cos(144°) negativ ist und gilt . ( ist nicht möglich, da kein Null ist.)

2. Fall: ind = 2: Hier reicht es zu zeigen, dass der x-Wert von
kleiner ist als der x-Wert 1 + cos(72°) von und . Dies ist wahr, denn cos(72°) ist positiv und
aus und folgt und damit
.

Wegen kann man auch hier den 3. und
4. Fall auf den 1. und 2. zurückführen. Damit ist der Satz bewiesen.


sei ein 5-Tupel ganzer Zahlen. Der Vektor
gibt genau dann einen Punkt der nach de Bruijn konstruierten Penrose-Kachelung an, wenn es einen Punkt P
in der zugehörigen deBruijn-Kachelung gibt mit . Im
folgenden Satz wird ein Kriterium angegeben, mit dem die 5-Tupel N, die zu Punkten der Penrose-Kachelung
gehören, auf einfache Weise mit Hilfe der Fünfecke ausgesondert werden können. Dazu ist es sinnvoll,
die Ortsvektoren als komplexe Zahlen aufzufassen. Wir definieren dazu
mit der imaginären Einheit i. Der Index k, der bisher an v unten angesetzt wurde, wird jetzt als Hochzahl
benutzt, wobei ist, und zum Beispiel gilt. Das innere Produkt von N
mit dem 5-Tupel , nämlich , ist
dann eine komplexe Zahl, die bei geeignetem N einen Punkt der Penrose-Kachelung beschreibt.

Durch mit werden fünf 5-Tupel
mit besonderen Eigenschaften definiert. Dabei ist zu bedenken, dass ist, so dass gilt:
,
,
,
,
.
Wenn man die Komponenten bei Null beginnend abzählt, ist also die k-te Komponente von bei
die Komponente mit der Nummer 5-k, wobei man k=5 mit k=0 identifiziert. Das bedeutet, dass die
k-te Komponente von zu der k-ten Komponente von konjugiert komplex ist. .

Am inneren Produkte zweier dieser Tupel zeigt sich ihre wichtigste Eigenschaft:
falls und .

Statt des signierten Abstands eines Punktes P von der nächsten Gittergeraden
in Richtung betrachten wir jetzt den mit -1 multiplizierten Wert, um Zahlen zwischen Null und
1 zu bekommen. Den so erhaltenen Wert kann man als signierten Abstand der
Geraden von P ansehen. Das reellwertige innere Produkt ist dabei der Realteil der
komplexen Zahl und kann darum unter Verwendung der zu p konjugiert komplexen Zahl
durch beschrieben werden. ist das 5-Tupel aus diesen
Zahlen. Dabei werden Tupel komplexer Zahlen wie bei reellen Zahlen komponentenweise addiert und
auch so mit einer komplexen Zahl multipliziert. Sei
und das 5-Tupel reeller Zahlen mit der Summe Null, durch das ein Pentagrid
bestimmt wird, bei dem kein Punkt auf mehr als zwei Gitter-Geraden liegt. Dann wird das 5-Tupel der
signierten Abstände der k-ten Frontgerade von P beschrieben durch
.
Für P im Innern einer Kachel der de Bruijn-Kachelung sind diese Abstände positiv und kleiner als 1.


Satz 2 : N sei ein 5-Tupel ganzer Zahlen mit der Summe .
Dann sind folgende Aussagen äquivalent:

1) Es gibt eine komplexe Zahl p zu einem Punkt P im Innern einer Kachel des D-Pentagrids mit N = J(p).
2)

Beweis: Es sei zunächst N = J(p) vorausgesetzt. Dann folgt nach dem vorhergehenden Satz
.

Vorausgesetzt sei nun: Es gibt ein 5-Tupel L aus positiven reellen Zahlen kleiner als 1 mit der
Summe ind, so dass gilt. Dann ist und .
Da entsprechende Komponenten von konjugirt komplex zu denen von sind und die Komponenten
von reell sind, gilt auch .

Sei nun , also .
R sei die Matrix mit den Zeilen . R ist symmetrisch.
S sei die ebenfalls symmetrische Matrix, bei der diese Zeilen in der Reihenfolge stehen.
Dann ist die Matrix mit 5 an jeder Stelle der Hauptdiagonalen und sonst Nullen. Wegen

folgt
.
Dieses 5-Tupel sei B(p) genannt. Seine Komponenten sind die signierten Abstände des Punktes P zum
Ortsvektor p von den Ursprungsgeraden mit den Normalenvektoren . Wegen sind
die Komponenten von L darum die Zahlen j(k ; P) zu dem durch D bestimmten Pentagrid.