Es lebe die Geometrie!

Orthogonalität in der dreidimensionalen hyperbolischen Geometrie

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum I'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum II'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_II.pdf

In der dreidimensionalen hyprbolischen Geometrie wird die Orthogonalität von Ebenen über ihre
Beziehung zu der Kugel K vom Radius 1 um den Koordinaten-Ursprung bestimmt. Ebenen d und e,
die das Innere von K treffen, sind genau dann hyperbolisch orthogonal, wenn ihre Schnittkreise kd und ke
mit K sich euklidisch rechtwinklig schneiden. Dies ist genau dann der Fall, wenn der Pol von d bezüglich
K auf e liegt. (Der Pol von d ist der gemeinsame Punkt aller Tangentialebenen, die K in Punkten von kd
berühren.) Der Pol von e inzidiert dann auch mit d. Mit dieser Eigenschaft wird die Orthogonalität auch
für Ebenen definiert, die K nicht treffen. Der Pol einer derartigen Ebene e ist der Punkt P im Innern von
K, für den alle mit P inzidierenden Ebenen ihren Pol auf e haben. Der Pol einer Tangetialebene ist ihr
Berührpunkt P, und es sind alle Ebenen durch P dazu hyperbolisch orthogonal. Die Ebene, deren Pol P
ist, nennen wir 'die zu P polare Ebene'.

Die Bezeichnung 'hyperbolische Geometrie' hat sich historisch bei der Untersuchung hyperbolischer Ebenen
entwickelt, die sich aus dem Zweifel an Euklids fünften Postulats über parallele Geraden ergeben haben.
Siehe dazu den Text 'Die Pseudosphäre und die hyperbolische Geometrie'
https://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf.
Einen direkten Zusammenhang mit Hyperbeln oder Hyperboloiden gibt es nur in der zweidimensionalen
hyperbolischen Geometrie. Siehe dazu die Seite ' Hyperbel-Modell'. Der Zusammenhang zwischen der
dreidimensionalen und der zweidimensionalen hyperbolischen Geometrie zeigt sich geometrisch und
algebraisch in der entsprechenden Rolle von Kugel und Kreis.

Wir erweitern den affinen Raum, in dem zu jedem Punkt P ein Koordinaten-Tripel gehört,
zu einem projektiven Raum, in dem jeder Punkt P durch eine Koordinaten-Quadrupel
bestmmt wird, wobei für eine Zahl r ungleich Null das Quadrupel zum gleichen
Punkt gehört. Es dürfen aber nicht alle vier Zahlen gleich Null sein. Die Quadrupel mit vierter Koordinate
Null gehören zu 'unendlich fernen' Punkten. Die andern Punkte kann man durch ein Quadrupel mit vierter
Koordinate Eins beschreiben. Sie sind die Punkte des affinen Raumes. Ebenen bestimmen wir durch
Quadrupel in eckigen Klammern, wobei auch hier die gleiche
Ebene angibt. P liegt auf dieser Ebene genau dann, wenn gilt:
.

Der Pol einer Ebene mit dem Quadrupeln hat das Quadrupel . Die Ebene
mit dem Quadrupel ist darum dazu genau dann hyperbolisch orthogonal, wenn
ist. Vor dem vierten Summanden steht also ein Minus-Zeichen. Wenn
für Punkte P und Q mit den Quadrupel und die entsprechende
Gleichung gilt, dann nennen wir P und Q zueinander 'polar'. Das
bedeutet, dass die zu P polare Ebene mit Q inzidiert.

Die Schnittmenge zweier verschiedener Ebenen bestimmt eine Raumgerade. Geraden g und h sind genau
dann hyperbolisch orthogonal, wenn sie einen Punkt gemeinsam haben und g ganz in einer Ebene liegt,
deren Pol Punkt von h ist. h ist dann orthogonal zu dieser Ebene. g und h werden zueinander 'polar'
genannt, wenn der Pol jeder Ebene durch g auf h liegt. Siehe dazu ' Kreise auf der Kugel>Orthogonalität' .
Wenn P bzw. Q ein beliebiger Punkt auf g bzw. h ist und die Geraden zueinander polar sind, dann ist die
Verbindungsgerade j von P und Q orthogonal zu g und zu h. Wenn P der Fußpunkt des euklidischen Lots
vom Koordinaten-Ursprung auf g ist, dann trifft diese Lotgerade auch h euklidisch orthogonal in einem Punkt
Q. Das Produkt der Abständes von P und Q zum Ursprung ist dann gleich 1 und die Richtungsvektoren von
g und h stehen euklidisch senkrecht. Das euklidische Lot vom Ursprung auf g und h ist auch hyperbolisch
orthogonal zu g und zu h. Zueinander polare Geraden haben genau dann einen gemeinsamen Punkt, wenn
sie die Einheits-Kugel K in diesem Punkt berühren.

Diese Animation soll die geometrische Bedeutung zueinander polarer Geraden klären. Die rot markierte
Gerade durch den schwarzen Koordinaten-Ursprung trifft die mit gelben Mittelstreifen gezeichnete
Gerade g im Punkt P und die Gerade g* mit hellblauem Mittelstreifen im Punkt Q euklidisch orthogonal.
Dies wird durch durch das rote Parallelogramm in diesen Punkten ausgedrückt, das perspektivisch
verzerrtes Bild eines Quadrats ist. g und g* sind zueinander polar. Die Endpunkte der Strecke zu g liegen
auf der Kugel, die zu g* sind beliebig gewählt.

Die Animation besteht aus fünf Phasen. In Phase 1 wird eine Ebene um g* gedreht und ihr hellblauer
Schnittkreis k* mit K angezeigt. Die Ebene schneidet g im gelben Punkt R. Dieser ist als Quadrat
gezeichnet, um auszudrücken, dass g und die Gerade QR hyperbolisch orthogonal sind. Der Kugelkreis
k in der Ebene durch g und Q ist gelb markiert. Er schneidet den Kreis k* euklidisch orthogonal. Um
zu verdeutlichen, dass k* und g* stets gemeinsam in einer Ebene liegen, wird in Phase 2 ein hellblauer Punkt
S auf g* verschoben. R und die Berührpunkte der beiden Tangenten von S an k* sind dabei stets kollinear.
In Phase 3 wird ein gelber Punkt T auf g* bewegt und dabei die Ebene des Kreises k um g gedreht, ohne
dass sich etwas an der euklidischen Orthogonalität von k und k* ändert. Die Gerade RT ist stets
hyperbolisch orthogonal zu g und zu g*. Im weiteren Verlauf werden die Punkte T, S und R in ihre
Ausgangs-Orte zurückbewegt.

In dieser Animation sind die grüne Gerade g mit gelber Mittellinie und die Gerade g* mit hellblauer
Mittellinie polar zueinender. g und die rote Gerade h mit gelber Mittellinie sind als Strecken mit Endpunkten
auf der Kugel K gezeichnet. Es soll gezeigt werden, wie man die blaue Gerade j konstruiert, die im
Innern von K hyperbolisch orthogonal zu g und zu h ist. Wir nennen j 'hyperbolische Achse von g und h'.
Anders als bei der Betrachtung von g und h als euklidische Raumgeraden gibt es bei der Betrachtung als
hyperbolische Raumgeraden noch eine zweite Achse, nämlich die zu j polare Gerade.

Auf g bewegt sich der gelbe Punkt R, der in der Ebene e durch g* liegt. e wird dabei um g* gedreht. Dies zeigt
sich an der Veränderung des hellblauen Kugel-Schnittkreises. Wenn der gelbe Schnittpunkt S von e und h
auf der Kugelsehne zu h liegt, wird die Gerade RS durch eine gelbe Strecke angezeigt, die bis zum Schnittpunkt
T mit g* reicht. Für die Konstruktion von j werden die Positionen von R an den Orten R1 und R2 durch grüne
runde Punkte markiert, zu denen S auf einen der beiden Schnittpunkte von h mit K fällt. Der Schnittpunkt von
j und g ist dann der hyperbolische Mittelpunkt M von R1 und R2. Die Konstruktion dieses Mittelpunkts zeigt das
letzte Standbild der Gleitschau. Dabei muss man sich den schwarzen Kreis als Kugel-Schnittkreis der Ursprungs-
Ebene durch g vorstellen. (Die Abstands-Maße sind andere als in der Animation.) Der dort angezeigte zweite
hellblaue Punkt kann als 'äußerer Mittelpunkt' angesehen werden. Diesen würde man bei der Konstruktion
der zu j polaren zweiten Achse verwenden.

Man kann den Mittelpunkt M mit Hilfe des Verhältnisses seiner Abstände von den Schnittpunkten A und B von
g mit der Kugel berechnen. Denn das Quadrat dieses Teilverhältnisses ist das Produkt der entsprechenden
Teilverhältnisse der Punkte R1 und R2 auf der Kugel-Sehne AB.

Zur Berechnung des hyperbolischen Abstand zweier Punkte P und Q kann man die symmetrische Bilinearform
benutzen. Die zugehörige Quadratform
hat genau für die Punkte der Einheitskugel den Wert Null. Denn im Fall f(p;p) = 0 kann nicht Null sein, weil p
sonst das Null-Quadrupel aus lauter Nullen wäre. Deshalb kann man setzen, und dann ist f(p;p) = 0
äquivalent mit der Kugelgleichung . Wenn P und Q im Innern von K liegen, ist ihr hyperbolischer
Abstand durch den Betrag von 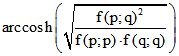gegeben, wenn P in K und Q außerhalb von K liegt
durch den Betrag von 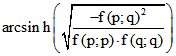. Für P und Q außerhalb von K definieren wir den Abstand
durch die Winkelgröße 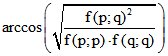, falls die Gerade PQ das Innere der Einheits-Kugel nicht trifft.
Andernfalls ist der Betrag des Terms unter dem Wurzel-Zeichen größer als 1; dann definieren wir den Abstand
durch .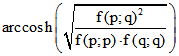

Etwas anschaulicher werden die beiden Terme mit arccosh und arcsinh, wenn man sie mit Hilfe eines
Doppelverhältnisses bestimmt, ein Verfahren, das auf Arthur Cayley (1821-1895) zurückgeht. Dazu
beschreibt man die Punktmenge einer K schneidenden Geraden g durch P und Q im affinen Raum mit
einem Stütz- und einem Richtungs-Vektor und einer Zahl r in der Form . Der hyperbolische
Abstand von P und Q ist dann gleich 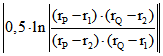, wobei und die r-Werte von P und
Q sind und und die der Schnittpunkte der Geraden durch P und Q mit der Kugel bzw. dem Kreis.


Zur Berechnung der hyperbolischen Achsen zweier Raumgeraden:

g und h seien zwei Raumgeraden, zu denen Plücker-Koordinaten in Form von Tripel-Paaren s = (s;t) und
u = (u;v) bestimmt sind. Siehe dazu die Erklärung am Schluss der Seite ' Höhen im 6-Rechteck'. Diese Tripel-
Paare wurden dort zu Tripeln mit dualen Zahlen umgewandelt, um die Berechnungen zu vereinfachen. An die
Stelle dualer Zahlen treten in der hyperbolischen Geometrie komplexe Zahlen. Wir ersetzen also das Tripel-
Paar s = (s;t) durch das Tripel , wobei
. Wenn h zu g polar ist, gilt

Wie für die euklidischen Raumgeraden kann auch für den hyperbolischen Raum ein erweitertes inneres Produkt
angegeben werden, das genau dann Null wird, wenn g und h hyperbolisch orthogonal sind, nämlich





Auch die Erweiterung des Kreuz-Produktes für reelle Zahlen zum Kreuz-Produkt für Dualzahlen, die
sich in der euklidischen Geometrie bewährt, lässt sich auf komplexe Zahlen übetragen. Es ist nämlich

wobei .
Für gilt zwar , aber wie in der euklidischen Geometrie ist m nicht
immer Tripel einer Geraden, weil die reelle Zahl möglicherweise nicht
Null ist. Man erhält aber ein Geraden-Tripel der Achse von g und h, wenn man m durch die komplexe
Zahl teilt oder für die dazu polare Achse durch . Auch hierbei kann also die
entsprechende Regel für euklidische Geraden übertragen werden. Wir bezeichnen und
als 'k-normierten Term zu m'. Diese Normierung ist nur dann möglich, wenn gilt.
In dem Fall nennen wir m k-normierbar. Im Fall ist m Tripel einer Geraden, welche die
Einheitskugel K berührt.