Es lebe die Geometrie!

Addition von geschlossenen Drehpunktkurven

Zu einer reellwertigen Funktion f mit dem Definitionsbereich mit einer natürlichen Zahl p
defininieren wir die zugehörige Drehpunktkurve durch . Wenn man
statt der komplexen Schreibweise kartesische Koordinaten benutzt, wird der Punkt durch das Paar

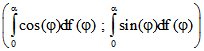
beschrieben. Damit die dabei benutzten Stieltjes-Integrale existieren, wird vorausgesetzt, dass die Variation
von f beschränkt ist, f sich also als Differenz zweier monoton wachsender Funktionen darstellen lässt. Wenn
f stetig differenzierbar ist, gibt das Koordinatenpaar 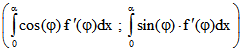den Punkt
mit Hilfe von riemannschen Integralen an. Die Verwendung des Stieltjes-Integrals ist unverzichtbar,
wenn durch die Drehpunktkurve auch Polygone erfasst werden sollen. In dem Fall ist f eine Treppen-
Funktion. Die Drehpunktkurve heißt 'p-geschlossen', wenn ist. Auch die zugehörige
Drehpunktfunktion nennen wir dann 'p-geschlossen'. Auf der vorliegenden Seite werden nur 1-geschlossene
Drehpunktkurven betrachtet. Andere Drehpunktkurven findet man auf der Seite 'Zykloidenkette 4'. Alle
Funktionen der Form oder sind 1-geschlossen, falls k eine natürliche Zahl
größer als 1 ist. Auch und sind 1-geschlossen, sowie alle linearen
Funktionen. Alle Linearkombinationen von 1-geschlossenen Funktionen sind ebenfalls 1-geschlossen.

Nach obiger Definition liegt der Anfang- und Endpunkt im Ursprung des Koordinatensystems.
Gelegentlich verschieben wir diesen Punkt. Dann muss in der Definition eine konstante komplexe Zahl
bzw. ein Paar konstanter reeller Zahlen hinzuaddiert werden.

Die Besonderheit der Drehpunktkurve besteht darin, dass die Gerade mit dem Richtungswinkel durch
der Punkt Tangente der Kurve ist, falls die Kurve hier differenzierbar ist. Wir sagen darum auch:
'hat den Richtungswinkel als Parameter'. Wenn man eine Gerade g zunächst im Punkt
mit dem Richtungswinkel 0, also in Richtung der Rechtsachse an die Drehpunktkurve anlegt und g dann an
der Kurve abrollt, bewegt sich der Drehpunkt von g längs dieser Geraden. Wenn für jeden Richtungswinkel
die Lage des Drehpunktes auf g wie auf einem Stab markiert wird, gibt den signierten Abstand
von der Lage des Drehpunktes zum Richtungswinkel 0 an. Wenn f also wächst, entfernt sich der Drehpunkt
auf g von der Ausganglage auf g, wenn sie fällt, nähert er sich wieder. Wenn die Drehpunktfunktion f für
einen Richtungswinkel ein Extremum hat, ergibt sich für die Drehpunktkurve eine Spitze. Falls f überall
monoton wächst, ist die Umfangslänge der Kurve. Wir erweitern die Definition der 'Umfangslänge'
auch für nicht monotone Drehpunktfunktionen, indem wir auch dann als 'Umfangslänge' bezeichnen.
Dort wo f fällt, werden die Längen von Kurvenstücken mit einem Minus-Zeichen versehen. Wenn die
Drehpunktfunktion eine Treppen-Funktion ist, haben an Sprungstellen mit fallenden f-Werten in dem
zugehörigen Polygon Seiten negative Längen.


Siehe dazu auch die Pdf-Datei Erklärung zur Drehpunktfunktion

Die Animation zeigt die grüne, rote bzw. blaue 1-geschlossene Drehpunktkurve zu der Drehpunktfunktion
, und . Es handelt sich um eine Astroide, eine
Spitzen-Evolvente der Astroide und um einen Kreis. Dabei ist . Die
Addition der Astroide und der Spitzen-Evolvente ergibt also einen Kreis. Die Umfangslänge der
Astroide beträgt f(360°) = 0 und die der Evolvente und des Kreises .
Die Umfangslänge der Drehpunktkurven-Summe stimmt also mit der Summe der Umfangslängen
der Summanden überein.

Da da Stieltjes-Integral linear im Integrator ist, gilt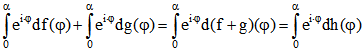
.
Darum ergibt sich der Ortsvektor von durch Vektor-Addition aus den Ortsvektoren von
und . Dies gilt für die erste Periode der Animation mit einem gemeinsamen Startpunkt für alle drei
Kurven im Koordinaten-Ursprung, aber auch für die zweite Periode, in der der Startpunkt der roten
Kurve auf der grünen Astroide in den Punkt verschoben wurde. In jedem Fall sind die Tangenten in
den Punkten , und parallel.

In der dritten Periode der Animation wird zusammen mit der grünen Kurve auf der roten Kurve
verschoben. Dabei ändert sich in diesem Punkt dieTangenten-Richtung der roten Kurve. Der Punkt der
grünen Kurve mit der gleichen Tangenten-Richtung ist dann Berühtpunkt der Astroide mit dem Kreis.
Der Kreis ist also Hüllkurve der verschobenen Astroiden. In der vierten Periode der Animation wird
gezeigt, dass Entsprechendes auch gilt, wenn die Startpunkte der drei Kurven zusammenfallen.

Die Bilder der Gleitschau nach der Animation sind Standbilder davon.

In dieser Animation wird zu der roten Astroide der grüne Kreis addiert und es entsteht die blaue
Spitzenevolvente der Astroide. Die zugehörigen Drehpunktfunktionen sind für den
Kreis und bzw. für die Astroide bzw. ihre Evolvente.

Hier wird die Spitzen-Evolvente der Astroide zur Drehpunktfunktion zu
einem gleichseitigen Dreieck mit dem Inkreisradius 1 addiert, zu dem die Drehpunktfunktion
gehört, deren Graph aus drei Treppenstufen besteht.
Damit sich die Umfangslänge f(360°) des Dreiecks richtigerweise zu ergibt, darf nicht als
Sprungstelle definiert werden. Es ist also .

Zu dem roten Dreieck mit der Drehpunktfunktion
wird das grüne Quadrat mit der Drehpunktfunktion addiert.

Das rote Viereck und das grüne Fünfeck werden zu dem blauen Neuneck addiert, wobei die
Startpunkte verschieden sind. In der zweiten Periode der Animation geben die Seitenpfeile die zu
den Seiten gehörigen Richtungswinkel an. Sie sind grau gefüllt, wenn die Drehpunktfunktion bei
einen Sprung nach unten macht. Wenn also die Drehpunktkurve für wachsendes
durchlaufen wird, folgt man bei den weiß gefüllten Pfeilen der Pfeilrichtung und bei den grau
gefüllten der Gegenrichtung. Die Pfeillänge stimmt mit der Sprungweite im Graphen der
Drehpunktfunktion überein.