Es lebe die Geometrie!

Stereografische Projektion beim Viereck
auf der Einheits-Kugel mit nicht komplanaren Eckpunkten

Eine stereografische Projektion ist eine Zentralprojektion einer Quadrik auf eine affine Ebene mit dem Zentrum
auf der Quadrik, aber nicht auf der affinen Ebene. Dabei gibt es zum Zentrum N keinen Bildpunkt. Wenn die
Quadrik eine Kugelfläche ist, kann jedem anderen Punkt P der Schnittpunkt P' der Geraden NP mit der affinen
Bildebene zugeordnet werden. Die Quadrik ist auf dieser Seite die Menge K der Punkte des dreidimensionalen
affinen Raums im Abstand 1 vom Ursprung mit dem Koordinaten-Tripel (0;0;0), und N ist der Punkt (-1;0;0).
Unsere Bildebene ist die Ebene x = 1, welche K im Schnittpunkt mit der x-Achse berührt.

Wie auf den beiden vorhergehenden Seiten betrachten wir ein Viereck ABCD auf K mit nicht komplanaren
Eckpunkten. Die Projektions-Bilder von A, B, C, D bezeichnen wir mit , , und . Es soll
dargestellt werden, wie man die Bilder , , und der Schnittpunkte Z0, Z1, Z2 und Z3 der sechs
gemeinsamen Lote gegenüberliegender Kanten des Vierecks mit Hilfe von Zirkel und Lineal in der Bildebene
konstruieren kann.

Im ersten Teil der vier Teile dieser Animation wird das Viereck ABCD um 90° um die y-Achse gedreht. Im
ersten Bild ist dabei der schwarze Punkt N mit dem Koordinaten-Tripel (-1;0;0) duch den Ursprung mit dem
Tripel (0;0;0) verdeckt, die Ebene x = 1 ist parallel zur Bildschirm-Ebene und die y-Achse verläuft von links
nach rechts. Die eingezeichneten farbigen Kegelschnitte ergeben sich, wenn man die Fußpunkte der Lote von
Z1 auf die Seiten-Ebenen des Vierflachs ABCD um Achsen durch Z1 hyperbolisch dreht, also um gemeinsame
Lotgeraden gegenüberliegender Kanten von ABCD. (Z1 ist als grünes Quadrat mit weißem Kern eingezeichnet,
die Achsen als dünne Linien in den Farben magentarot, hellgrün und hellblau.)

Nach der Drehung des ersten Teils blickt man auf die 'Kante' der Ebene E mit der Gleichung x = 1, auf die
im zweiten Teil stereografisch projiziert werden soll. Dazu wird jeder gezeichneten Punkt P längs seiner
Verbindungs-Geraden mit dem Projektions-Zentrum N in seinen Bildpunkt P' auf E verschoben. Der
jeweilige Zwischenpunkt teilt die Strecke PP' für alle Punkte im gleichen Verhältnis. Drei anfangs kollineare
Punkte P, Q und R haben dabei im Allgemeinen nicht kollineare Zwischenpunkte. Darum sind im Übergangs-
Prozess die farbigen Kurven keine Kegelschnitte, wohl aber im Endzustand auf der Bildebene E, weil P', Q'
und R' dann kollinear sind.

Im dritten Teil der Animation wird die Ebene E zusammen mit dem Bild der stereografischen Projektion um
90° um die y-Achse zurückgedreht, sodass im Schlussbild dieses dritten Teils das Projektions-Bild unverzerrt
erscheint, weil E parallel zur Bildschirm-Ebene liegt. Im vierten Teil wird in dieser Sicht der Prozess des
zweiten Teils rückwärts durchlaufen.

Die Gleitschau soll zeigen, wie man ausgehend von vier Bildpunkten der Eckpunkte von ABCD die
Bildpunkte innerhalb der Ebene E mit Zirkel und Lineal konstruieren kann. Das Hauptproblem ist
dabei die Konstruktion der Projektions-Bilder von den Fußpunkten der Achsen auf den Kanten-Geraden von
ABCD, die in dieser und den beiden vorangehende Seiten als farbige Quadrate mit weißem Kern gezeichnet
wurden. In den ersten beiden Bildern der Gleitschau wird dieses Teilproblem zunächst herausgehoben, und zwar
im ersten Bild für die Fußpunkte im dreidimensionalen Raum und im zweiten für das entsprechende Bild bei der
stereografischen Projektion. Anschließend wird die Konstruktion von ausgehend von in
einer Folge von 16 Bildern dargestellt.

Das erste Bild zeigt ABCD in dreidimensionalen Raum zusammen mit dem grünen Umkreis vom Seiten-Dreieck
ACD und dem gelben Umkeis von ABC . Die Pole der Umkreis-Ebenen sind in gleicher Farbe als umrandete
Punkte eingezeichnet. Die Ebene durch den grünen Pol P1 und die Kante AD ist hyperbolisch orthogonal zur
Ebene ACD, und darum ihr Schnittkreis mit K euklidisch orthogonal zum Umkreis von ACD. Die Tangente
des grünen Umkreises von ACD ist darum euklidisch orthogonal zur Geraden DP1. Diese Tangente schneidet
die Kanten-Gerade AC im gelben Punkt Q1. Die Polare von Q1 bezüglich des grünen Umkreises von ACD ist
die schwarze Gerade, welche AC hyperbolisch orthogonal im gelben Punkt R1 schneidet. Mit vertauschten
Rollen von 'grün' und 'gelb' konstruiert man analog die Punkte P2, Q2 und R2. Der hyperbolische Mittelpunkt
von R1 und R2 ist Schnittpunkt einer Achse g mit der Kanten-Gerade AC. Der dazu polare Punkt auf AC ist
der Schnittpunkt von AC mit der zu g polaren Achse. Diese Konstruktion wurde in etwas variierter Form auf
der Seite ' Orthogonalität' dargestellt. Dort wird am Schluss der zweiten Gleitschau gezeigt, wie man den
hyperbolichen Mittelpunkt konstruiert. Diese Konstruktion kann sowohl mit dem gelben wie auch dem
grünen Umkreis als Basis-Kreis durchgeführt werden.

Das zweite Bild der Gleitschau zeigt das Bild des ersten bei stereografischen Projektion in die Ebene E parallel
zum Bildschirm. Die Bilder der Kreise sind Kreise mit dem Bildpunkt ihres Poles als Mittelpunkt, bei denen die
euklidischen Größen der Winkel für Urbilder und Bilder gleich sind. Darum sind beide Umkreise euklidisch
orthogonal zu den beiden anderen farbigen Kreisen. Im dritten bis siebenten Bild wird das zweite schrittweise
aufgebaut, dann im achten bis dreizehnten Bild die Mittelpunkts-Konstruktion eingefügt. Das vierzehnte Bild
ergänzt alle analog konstruierten Achsen-Fußpunkte und das fünfzehnte ihre Verbindungen.

Die letzten drei Bilder der Gleitschau mit allen Achsen und Schnittpunkten erklären im Text
die Berechnung dieser Schnittpunkte als Affinkombination der Koordinaten-Tripel von . Die
Koeffizienten ergeben sich aus den Längen der Strecken , , , , , ,
die mit bezeichnet sind. Dabei werden die Längen jeweils dreier Strecken multipliziert,
die zu einem Teil-Dreieck des Vierecks gehören. Dies ergibt sich aus der Formel
am Schluss der Seite ' Kugelviereck 1'.

Im 16. Bild wird jedes Projektions-Bild einer Achsen durch von einem gleichfarbigen Kreis geschnitten.
Die beiden weißgefüllten Schnittpunkte sind die Projektions-Bilder der Kugel-Punkte auf der Achse. Der
Kreis-Mittelpunkt liegt auf der polaren Achse in gleicher Farbe. Er ist Projektions-Bild des Pols der
Ebene durch zwei Punkte des Basis-Vierecks ABCD, die hyperbolisch orthogonal zur Ebene durch
die beiden Punkte von ABCD und ist. Die Projektions-Bilder der beiden gleichfarbigen Achsen sind
euklidisch orthogonal, weil die beiden Ebenen durch diese Achsen und das Projektions-Zentrum (-1;0;0)
hyperbolisch orthogonal sind und darum K in euklidisch orthogonalen Kreisen schneiden.

Zur stereografischen Projektion des dreidimensionalen hyperbolisch-projektiven Raums :

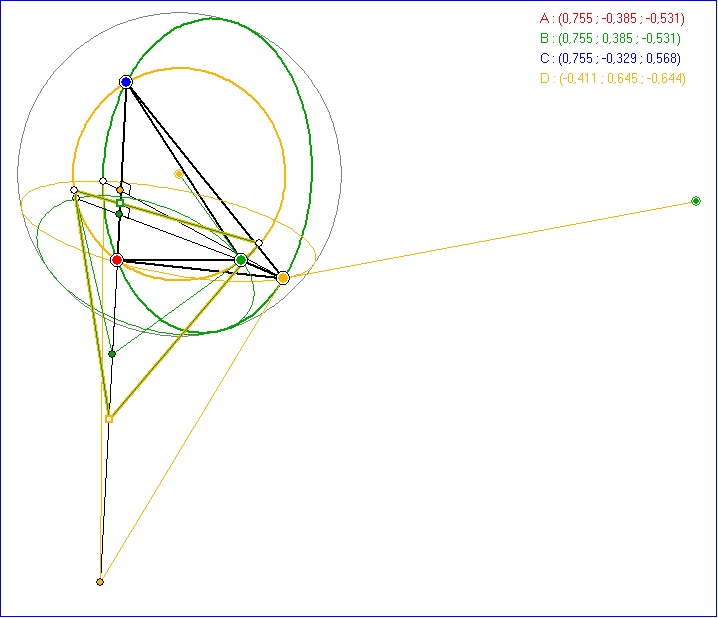
Zu einem Quadrupel definieren wir . Dann ist die
durch das hochgestellte s bestimmte Zuordnung eine lineare Abbildung des vierdimensionalen reellen
Vektorraums mit dem Kern . Wenn v nicht Element des Kerns ist, beschreiben v und
Punkte des dreidimensionalen projektiven Raums. Die Abbildung ist eine Abbildung der Punkte
des dreidimensionalen projektiven Raums mit Ausnahme des Punktes mit dem Quadrupel (-1;0;0;1). Wenn
Tripel eines Punktes P im affinen Unterraum ist mit und das
zugehörige Quadrupel, dann wird P in den Punkt mit dem Quadrupel und
dem Tripel 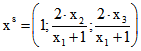abgebildet, der mit P und der Projektions-Zentrum N zum Tripel
kollinear ist. Wenn U der Punkt mit dem Tripel (1;0;0) ist und den euklidischen Abstand von U und
bezeichnet, dann teilt P die Strecke im Verhältnis .

Die Abbildung ordnet jedem Punkt Q der
affinen Ebene E das Quadrupel eines von N verschiedenen Punktes P der Einheits-Kugelfläche K zu, der
mit N und Q kollinear ist. Das zu P gehörige Tripel ist 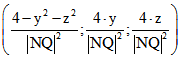. Für alle Punkte P
ungleich N in K gilt : , und für alle Q in E gilt .

Vier von N verschiedene Punkte auf K liegen genau dann gemeinsam in einer Ebene D, wenn ihre s-Bilder
kollinear oder konzyklisch sind, also alle vier auf einer Geraden oder einem Kreis liegen. Der erste oder
zweite Fall tritt ein, je nachdem, ob N in D liegt oder nicht. Im zweiten Fall ist das s-Bild des Pols von D
der Mittelpunkt des Bild-Kreises.

A und B zu Tripeln a und b seien von N verschiedene Punkte auf K. und seien ihre stereografischen
Bilder mit den Tripeln und . Ein Punkt P teile die Strecke AB im Verhältnis v, und ein Punkt Q teile die
Strecke im Verhältnis w. Q ist genau dann stereografisches Bild von P, wenn
gilt, denn dann ist .
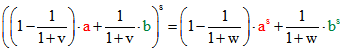Wenn also zu einem Punkt P des Raums eine durch P verlaufende Gerade bekannt ist, die K in zwei Punkten
A und B schneidet, dann ist die Lage von P nicht nur durch das Teilverhältnis v auf AB vollständig bestimmt,
sondern auch durch das Teilverhältnis für die stereografischen Bilder. Dies ermöglicht die Darstellung
räumlicher Konfigurationen in der Ebene ohne Verlust von Information.

Wenn eine Ebene D, die A und B enthält, um AB gedreht wird, bewegt sich ihr Pol auf der zu AB polaren
Gerade. Da das stereografische Bild des Schnittkreises von D mit K ein Kreise in E ist, dessen Mittelpunkt
das stereografische Bild des Pols von D ist, ist die Mittelsenkrechte der Strecke AB das stereografische
Bild der Polaren von der Geraden AB.

A, B, C und D zu Tripeln a, b, c und d seien vier nicht komplanare Punkte von K, und keiner davon N.
Dann kann das Tripel jedes Punktes P des affinen Raums als Affinkombination
dargestellt werden mit reellen Zahlen r, s, t, u, deren Summe 1 ist, wobei diese vier Zahlen eindeutig
bestimmt sind. ist dann im Allgemeinen verschieden von P, liegt aber auf der Geraden NP.
mit dem Tripel bezeichne das s-Bild von A und Entsprechendes gelte für die Bilder
von B, C und D. Sei , ,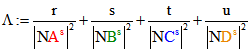
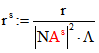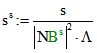
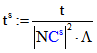und 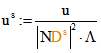. Dann ist und hat das Tripel
. Dabei ist das Tripel
von P. Die Strecke wird durch P also im Verhältnis
geteilt. ist stets ein Punkt von K, nicht aber P selbst. Diese beiden Punkte stimmen genau
dann überein, wenn gilt:
.



Zur Berechnung der Koordinaten von , , und :
Die Tripel der s-Bilder von A und B seien und . Dann hat A das Quadrupel
und man errechnet

Nach den Erklärungen am Schluss der Seite ' Kugelviereck 1' ergibt sich für das Quadrupel von Z3 der Term


Hierbei ist , da bei die 4. Komponente zu 1 normiert wurde. Wenn man darum
den Term für Z3 mit und die analogen Terme für b, c und d multipliziert, erhält man


Der gemeinsame Faktor 32 kann hier weggelassen werden, da Quadrupel x und rx mit einer reellen Zahl r
ungleich Null denselben Punkt beschreiben. Nach Anwendung der stereografischen Projektion und Teilung
durch die vierte Komponente erhält man dann für das Tripel von den Term



Man erhält die Terme für die drei anderen Zentren, indem man in den Summen an zwei Stellen im Zähler und
im Nenner das Plus-Zeichen in ein Minus-Zeichen umwandelt.