Es lebe die Geometrie!

Gangpolkurven bei Koppelgetrieben

Zur Erklärung des Begriffs 'Gangpolkurve':

Man stelle sich eine Scheibe vor, die so über einer Zeichenebene bewegt wird, dass alle ihre Punkte
stets den gleichen Abstand von der Ebene haben. In jedem Augenblick gibt es dann einen Punkt auf
der Scheibe, der die Geschwindigkeit Null hat, vorausgesetzt, dass die Scheibe groß genug ist und
die Bewegung keine momentane Verschiebung ist. Dies ist der 'Momentanpol'. Die Spur dieses
Momentanpols in der Zeichenebene heißt 'Rastpolkurve' und die Spur auf der Scheibe 'Gangpolkurve'.
Im Allgemeinen haben diese Kurven eine unterschiedliche Form. (Unten auf der Seite werden zwei
Beispiele mit gleicher Form dargestellt.) Im Zusammenhang mit einem Koppelgetriebe stelle man
sich vor, dass die Scheibe fest mit der Koppel verbunden ist.

Wenn man die Gangpolkurve in jedem Augenblick auf die Zeichenebene überträgt, wie einen Schatten
bei senkrechter Beleuchtung, falls die Scheibe durchsichtig ist, dann haben die Rastpolkurve und die
Schatten-Gangpolkurve in jedem Augenblick den Momentanpol gemeinsam. Bemerkenswert ist dabei,
dass sich die Rastpolkurve und die Schatten-Gangpolkurve im Momentanpol stets berühren. Bei der
Bewegung der Scheibe rollt die Schatten-Gangpolkurve ohne zu Rutschen an der Rastpolkurve ab.
Dies soll im Folgenden am Beispiel der symmetrischen Schwingkurbel und des Zwillingskurbelgetriebes
gezeigt werden.

Bei den Koppel-Getrieben der beiden Animationen haben die Arme jeweils die Längen 1 und 2.
In der oberen Animation ist der Abstand zwischen den Endpunkten A und B der Koppel 1 und
der Abstand der Führungskreis-Mitten M1 und M2 gleich 2. In der unteren Animation ist es
umgekehrt. In beiden Fällen bilden M1, M2, B und A ein Drachen-Viereck. Die dunkelgrüne
Gangpolkurve der oberen Animation hat die gleiche Form wie die hellgrüne Rastpolkurve der
unteren Animation, und umgekehrt. Auf der vorherigen Seite wird gezeigt, dass beide Kurven
pascalsche Schnecken sind.

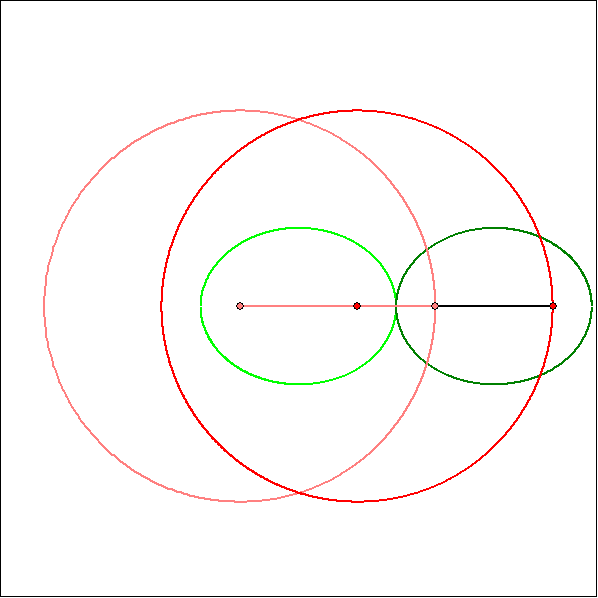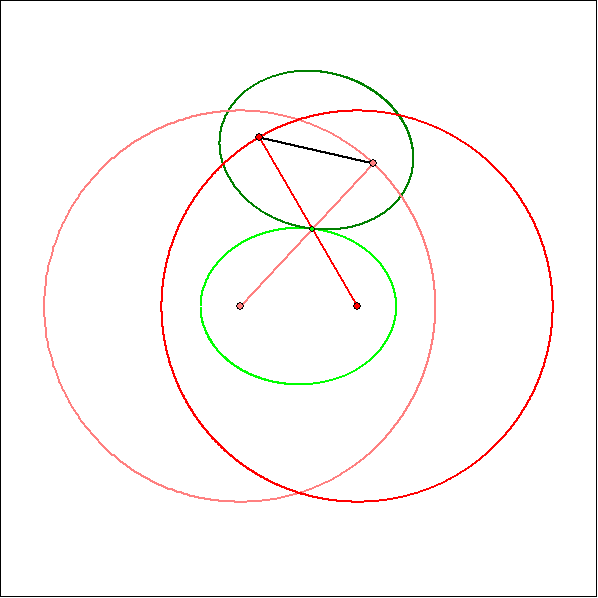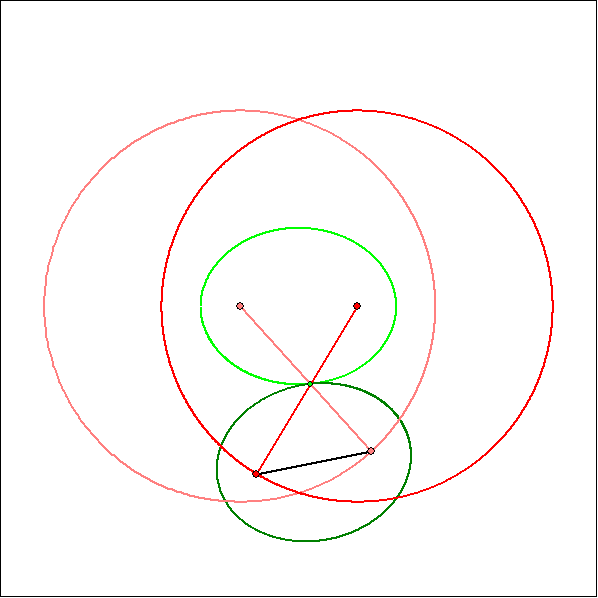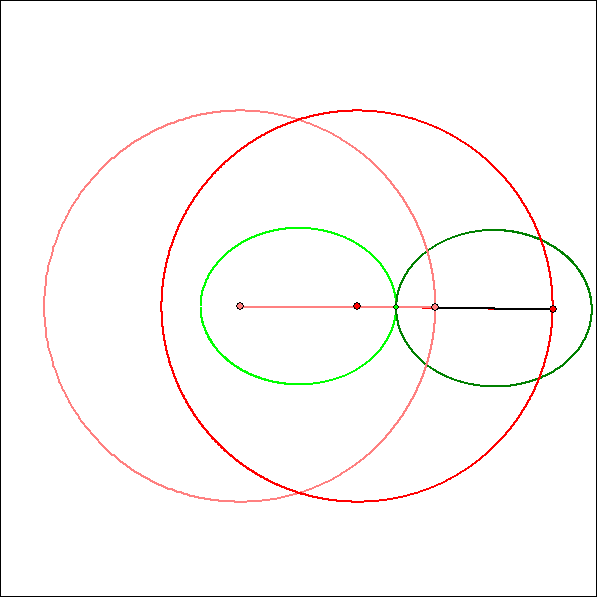
Bei einem Zwillings-Kurbelgetriebe stimmt die Koppellänge AB mit dem Abstand der
Führungskreis-Mitten M1 und M2 überein und auch die Armlängen sind gleich. Darum
haben die Gangpolkurve und die Rastpolkurve die gleiche Form, Beim gleichläufigen
Zwillings-Kurbelgetriebe, bei dem die Koppellänge kleiner als die Armlänge ist, sind die
Kurven kongruente Ellipsen, die aneinander abrollen.

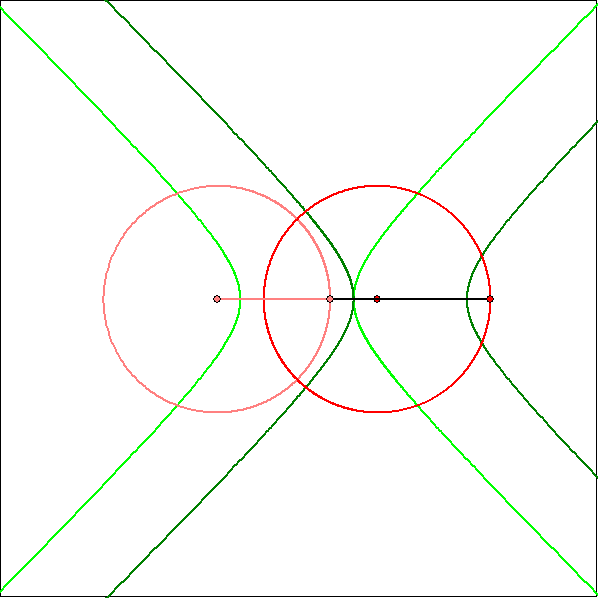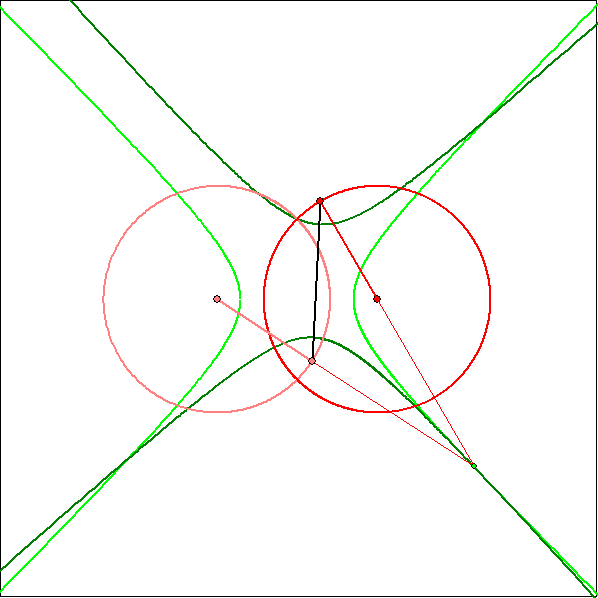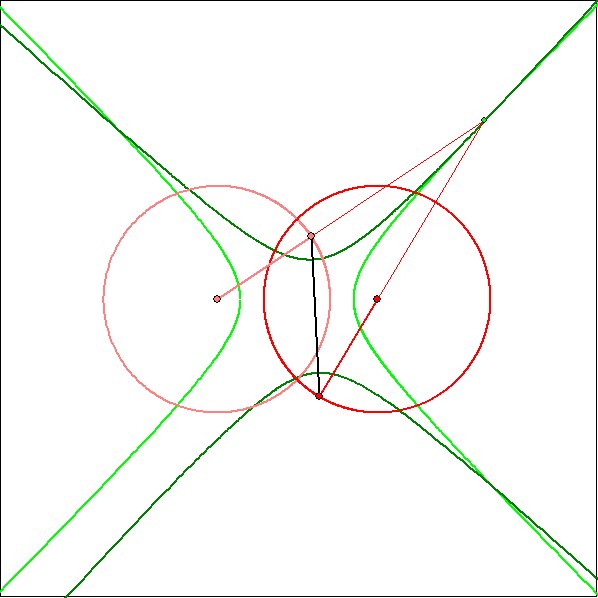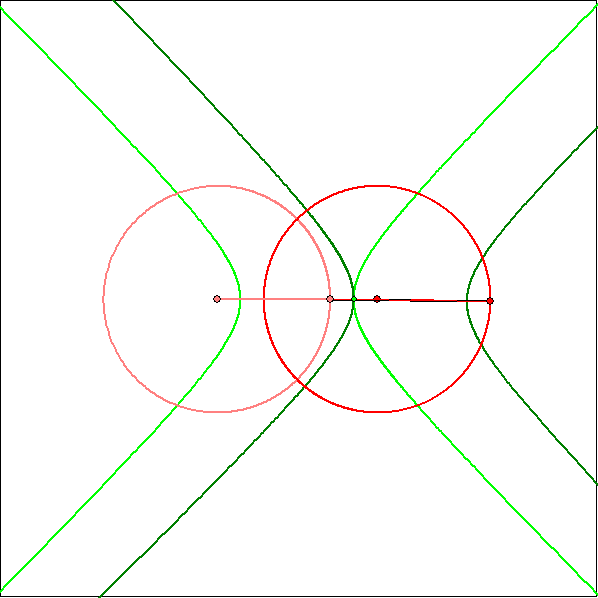
Beim gegenläufigen Zwillings-Kurbelgetriebe ist die Koppellänge größer als die Armlänge.
Darum sind die Rastpolkurve und die Gangpolkurve aneinader abrollende kongruente Hyperbeln.

Die Animation zeigt die Gangpolkurve eines Koppelgetriebes mit den Armlängen 1 und 1,23,
der Koppel-Länge 1,512 und dem Abstand 1,65 der Kreis-Zentren.

Zur Begründung, dass die Gangpol-Kurve ohne zu Rutschen an der Rastpol-Kurve abrollt:

In der Zeichen-Ebene, die wir als feststehendes 'Rast-Ebene' ansehen, sei ein euklidischen Koordinaten-
System gegeben, in dem wir jedem Punkt P ein Koordinaten-Paar zuordnen, das wir als
komplexe Zahl betrachten mit . Dann hat der Punkt P', der aus P durch Drehung
um den Ursprung (0;0) mit dem Drehwinkel gegen den Uhrzeiger-Sinn entsteht, die Koordinaten-Darstellung
, wobei i die eulersche Zahl ist. Wir legen den Koordinaten-Ursprung
der Rast-Ebene in den ersten Dreh-Punkt M1 des Koppel-Getriebes und den zweiten Dreh-Punkt Punkt M2
auf die -Achse.

In der bewegten Gang-Ebene benutzen wir ein euklidischen Koordinaten-System mit dem Koordinaten-Paar
mit der zugehörigen komplexen Zahl . Der Ursprung dieses Systems liege im
Anfangspunkt der Koppel A und der Koppel-Endpunkt B sei Punkt der -Achse. Die Größe des
Drehwinkels der -Achse AB gegenüber der -Achse M1M2 sei genannt. Zu A im Abstand von
M1 gehört beim Drehwinkel gegenüber der -Achse im Rast-System die komplexe Zahl
und im Gang-System die komplexe Zahl 0 . Zu B im Abstand s vom M2 gehört beim Drehwinkel der Sehne
gegenüber der -Achse im Rast-System die komplexe Zahl . Im Gang-System gehört zu B die
Zahl s. Ein Punkt Z, der im Gang-System die komplexe Zahl hat, hat im
Rast-System die komplese Zahl .

Zur Beschreibung einer Bewegung eines Punktes, zu dem im Gang-System die gangfeste Zahl gehört,
gehen wir von zeitabhängigen Funktionen und mit den Ableitungen und
aus. Dann gibt die zeitliche Abhängigkeit des Punktes Z im Rast-System an
mit der Ableitung . Für einen Momentan-Pol Z ist die Geschwindigkeit
Null, folglich . Wir betrachten nur den Fall , da sonst der Momentan-Pol
im Unendlichen liegen würde. Dann ist die komplexe Zahl zum
Momentanpol (gemessen im im Gang-System) zum Zeitpunkt t und

die komplexe Zahl zum Momentanpol (gemessen im Rast-System).
Der Geschwindigkeits-Vektor ergibt sich in beidenSystemen durch Ableitung nach der Zeit :


und

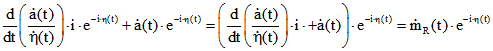
Es ist also , wobei der Faktor sich daraus ergibt, dass die -Achse gegenüber
der -Achse um gedreht ist. Wegen sind die Vektoren und gleich lang.
Die Rastpol-Kurve und die Gangpol-Kurve werden
zwischen den Teitpunkten und vom Rastpol bzw.Gangpol vom gleichen Punkt durchlaufen und die
in beiden System gemessene Bogenlänge ist wegen 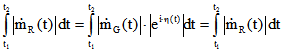gleich.
Darum rollt die Gangpol-Kurve ohne zu Rutschen an der Rastpol-Kurve ab.


.