Es lebe die Geometrie!

Die Kardioide als Kreisspiegelungs-Bild der Parabel

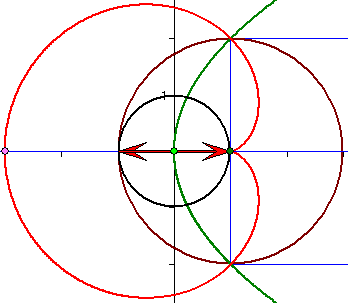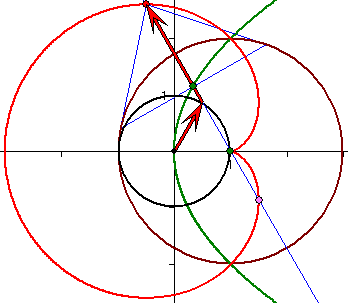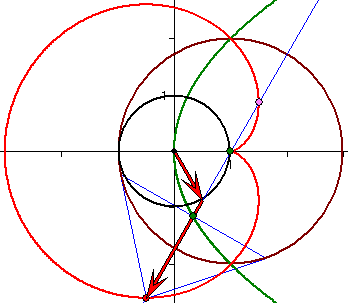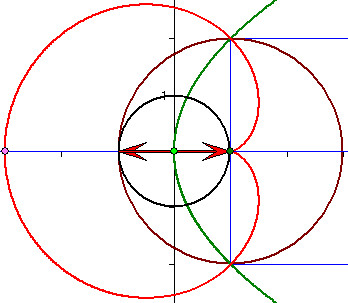
Abstände vom Brennpunkt
Durch Spiegelung der roten Kardioide an dem braunen
Kreis K um den Brennpunkt F(1 ; 0) mit dem Radius
1,5 entsteht die grüne Parabel (und umgekehrt). Die
blaue Polare zu einem Kardioiden-Punkt P außerhalb
von K (durch die beiden Tangentenberührpunkte auf K)
schneidet die Gerade PF im Parabelpunkt Q. Dabei
ist das Produkt der Streckenlängen von FP und FQ
gleich dem Quadrat des Radius.

Tangente und Distanzkreis
F ist sowohl Brennpunkt der Kardioide als auch der
Parabel. Bei der Kreisspiegelung wird ein Kreis durch
F in eine Gerade abgebildet und umgekehrt. Deshalb
ist das Bild jedes Berührkreises der Kardioide durch
F ('Distanzkreis' genannt) eine Parabel-Tangente. Der
Fußpunkt L des Lots von F auf die Tangente liegt auf
der Scheiteltangente. Folglich liegt das Bild von L auf
dem Distanzkreis durch die Mitte des Kardioidenbogens.
Das Bild einer Kardioiden-Tangente ist ein Berührkreis
durch F.

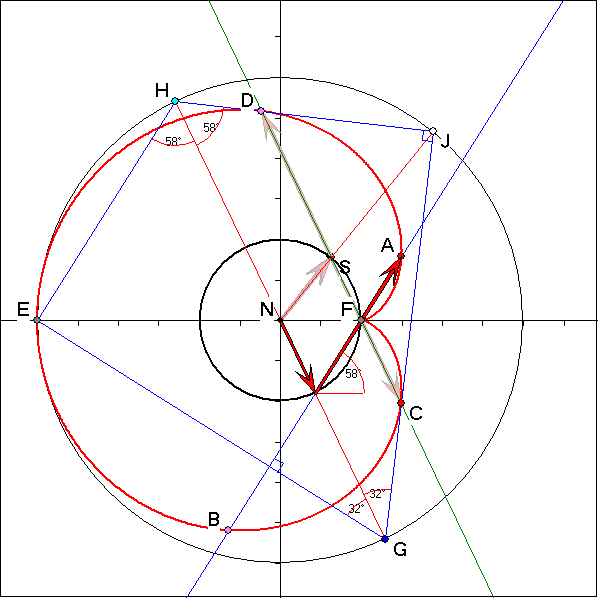
Winkelbeziehungen und Reflexion

Bild 1 der obigen Slideshow: Der Punkt A der Kardioide gehört zu dem langen roten Pfeil mit dem
Richtungswinkel und dem kurzen Pfeil mit dem Richtungswinkel .
Die Gerade CD verläuft parallel zum kurzen Pfeil durch N. Darum liegt der Punkt C bzw. D an der Spitze
des langen Pfeils, wenn dessen Richtungswinkel bzw. beträgt. Für
einen Richtungswinkel bzw. der Tangente in C bzw. D gilt , bzw. . Daraus
folgt, dass die Tangenten in C und D orthogonal sind, denn .
Die Strecke CD hat die Länge 4 und den Mittelpunkt S .
Wegen hat
die Gerade SJ den Richtungswinkel . Darum verläuft die
Gerade SJ durch N. G bzw. H sei der Schnittpunkte der Tangente in C bzw. D mit der Ursprungsgeraden
g durch den kurzen roten Pfeil. Nach dem Strahlensatz haben dann G und H den Abstand 3 von N, liegen
also auf dem Kreis um N durch die Bogenmitte E der Kardioide. J entsteht durch Spiegelung von E an g,
denn . Die Geraden FA und EG sind orthogonal, weil ein
Richtungswinkel von EG die Größe hat.

Bild 2 : Die grüne Parabel mit der Gleichung entsteht durch Spiegelung der Kardioide mit
der Gleichung an dem braunen Kreis mit der Gleichung ..

Begründung: Bei der Spiegelung am Einheitskreis um den Ursprung (0 ; 0) wird der Punkt zur komplexen
Zahl z in den zur komplexen Zahl abgebildet, bei Spiegelung an einem doppelt so großen Kreis
also in . Bei Verschiebung des Kreises um 1 nach rechts ergibt sich dann die Zuordnung
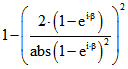. Für ist das Bild also . Für den Term in
der Klammer errechnet man . Für das Bild ergibt sich der
Term . Der zugehörige Punkt mit den kartesischen Koordinaten
liegt auf der Parabel .

Eigenschaften der Parabel :
Strahlen, die von rechts parallel zur Rechtsachse auf die Parabel treffen, werden in Richtung des
Brennpunkts F(1 ; 0) umgelenkt.
Der Fußpunkt des Lots vom Brennpunkt auf eine Tangente liegt auf der Scheitel-Tangente x = 0.
Wenn die Berührpunkte zweier Tangenten mit dem Brennpunkt kollinear sind, dann schneiden sie
sich auf der Leitgeraden x = -1.

Bild 3 : Der Kehrwert der Steigung im Punkt C' stimmt mit der Hälfte des y-Werts
von C' überein. Darum ist Richtungswinkel der Tangente in C'. Diese Tangente ist
folglich parallel zur Geraden EG. Entsprechend ist die Tangente in D' parallel zur Geraden EH.

Bild 4 : Die Spiegelung an dem braunen Kreis bildet eine Gerade in einen Kreis ab, der eine Parallele
zu g durch F in F berührt. Umgekehrt werden derartige Kreise in Geraden abgebildet. Dabei stimmen
die Winkelgrößen zwischen Bildern und Urbildern überein. Deshalb treten bei A und A' die gleichen
Winkelgrößen auf.

Bild 5 fasst alle bisherigen Winkelbeziehungen zusammen.

Bild 6 zeigt wie in Bild 3, dass der Winkel, unter dem ein Strahl von rechts auf die Parabel auftrifft,
halb so groß ist wie der Steigungswinkel der Geraden durch Brennpunkt und Auftreffpunkt. Analog
zu Bild 4 wird dargestellt, dass die gleichen Winkelgrößen wie bei A' auch bei A auftreten (Sorry, hier
wurde der Nebenwinkel markiert). Zusätzlich wird eine weitere Eigenschaft de roten Kreises K durch
A deutlich, der die x-Achse in F berührt und Bild der Parallelen zur x-Achse durch A' bei der
Kreisspiegelung ist: F und A liegen spiegelbildlich zur Rastkreis-Tangente im weiteren Schnittpunkt
neben F von K mit dem Rastkreis. Das bedeutet, dass die Kardioide der geometrische Ort der
Spiegelbilder von F an den Tangenten des Rastkreises ist.