Es lebe die Geometrie!

Winkel und Abstand von Kreisen

Die symmetrische Bilinearform ,
die am Schluss der vorhergehenden Seite zur Definition der Spiegelungen im dreidimensionalen
projektiv-metrischen Raum benutzt wurde, verwenden wir auch für die Definition von Winkel-Größen
und Abstände bei Kreisen in der x-y-Ebene. Dabei stimmen die Winkel-Größen mit denen überein,
die sich aus der euklidischen Maß-Bestimmung in der x-y-Ebene ergeben. Die Abstände kommen
dagegen in der euklidischen Geometrie nicht vor. Sie gehören zur hyperbolischen Geometrie. In der
folgernden Animation wird gezeigt, wie dieser 'hyperbolische Abstand' sich auf euklidische Abstände
zurückführen lässt

Dem Kreis KA mit dem Zentrum A(x;y) und dem Radius r haben wir im dreidimensionalen affinen Raumes
den Punkt RA(x;y;z) zugeordnet, für den ist. Zu den Null-Kreisen vom Radius Null, die
wir in der x-y-Ebene den Punkten zuordnen, gehören dann die Punkte des Paraboloids Par mit der Gleichung
. Jeder Raum-Punkte darüber gehören zu einem 'reellen' Kreis mit reellem Radius r > 0 und
jeder darunter zu einem 'imaginären' Kreis mit dem rein-imaginären Radius mit r > 0. Den Raum-Punkt
auf der Parallelen zur z-Achse durch den Punkt
nennen wir Anti-RA. Der Null-Kreis zum Punkt A gehört dann zum euklidischen Mittelpunkt von RA und
Anti-RA. Die Zeichnungen der zugeordneten Kreise zu RA und Anti-RA unterscheiden sich nur darin, dass
wir den imaginären Kreis zu Anti-RA in hellerer Farbe zeichnen.

Das Koordinaten-Tripel (x;y;z) eines Punktes P des dreidimensionalen affinen Raum erweitern wir zu dem
Quadrupel (x;y;z;1), das P im dreidimensionalen projektiven Raum beschreibt, in dem die 'unendlich fernen'
Punkte die vierte Komponente Null haben. Wenn u eine reelle Zahl ungleich Null ist, beschreibt das
Quadrupel den gleichen Punkt P. Quadrupel, die sich nur in einem Faktor ungleich
Null unterscheiden, werden also identifiziert. Ein Quadrupel mit beschreibt also
den Punkt zu Tripel .

Ein Quadrupel p nennen wir f-normiert oder fn-Quadrupel, wenn f(p;p) gleich 1 oder -1 ist. Jedes Quadrupel
p mit ungleich Null kann dadurch f-normiert werden, dass man es durch
teilt. Wenn sich 1 ergibt, gehört P zu einem reellen Kreis , andernfalls zu einem imaginären. f(p;p) ist das
Quadrat vom reellen bzw. imaginären Radius des zu P gehörigen Kreises.

Zur Berechnung von Winkeln und Abständen benutzen wir die Funktion .
Für Kreise um mit dem Radius und um mit dem Radius
ist
,
also .
Dieser Wert stimmt für reelle Radien mit dem Kosinus-Wert der euklidischen Größe des Winkels zwischen
der beiden Kreisen überein, falls sie Punkte gemeinsam haben. Andernfalls ist der Betrag von fn(p;q)
größer als 1 oder fn(p;q) rein-imaginär. In beiden Fällen ist arccos(fn(p;q)) bis auf ganzzahlige Vielfache von
rein-imaginär.Dann deuten wir den Imaginär-Teil davon als 'Abstand' der beiden Kreise und auch der
Raumpunkte. Wir definieren:


Die folgende Animation stellt die Maß-Beziehungen im räumlichen Zusammenhang mit Zahlen dar. Dabei sind
die angezeigten Abstände von Punkten P und Q am markierten Mittelpunkt von PQ fixiert.

Im ersten Teil der Animation wird der Raum-Punkt RP1 zum Kreis K1 um P1 auf der roten Raum-Geraden
g bewegt, ohne den Raum-Punkt RP2 auf g zum Kreis K2 um P2 zu verändern. Dabei ändern sich die
Schnittpunkte von K1 und K2 nicht. Ihre Koordinaten sind unten auf dem Bild angegeben. Die Größe des
Schnittwinkels der Kreise kann mit dem Kosinus-Satz im Dreieck in der x-y-Ebene mit den Eckpunkten P1,
P2 und einem der beiden Kreis-Schnittpunkte berechnet werden. Dabei bestätigt sich die oben behauptete
Berechnung mit Hilfe der Bilinearform f.

Im ersten Bild des zweiten Teils der Animation wird die schwarze Parallele c zur z-Achse hinzugefügt, die wir
'Zentrale' von g nennen. c trifft g in dem Punkt C, der auf g von der Parabel, in der die Ebene durch g parallel
zur z-Achse Par schneidet, minimal entfernt ist. g wird im zweiten Teil längs c nach unten verschoben, ohne
die Position von RP1, RP2 und C auf g zu verändern. Dabei rücken die Kreis-Schnittpunkte zusammen bis
sie aufeinander fallen, wenn g Par berührt. Wenn g Par anschließend in den zwei unten im Bild angegebenen
Punkten schneidet, gibt es keine Kreis-Schnittpunkte mehr. Es wird darum keine Winkel-Größe, somdern
der Abstand von K1 und K2 angezeigt. Wenn g Par schneidet, ist C Mittelpunkt der Schnittpunkte S1 und S2.

Im dritten Teil der Animation wird neben der Berechnung des hyperbolischen Abstands von Raumpunkten
oder Kreisen mit fn eine Bestimmung mit Hilfe des euklidischen Abstands von RP1 und RP2 zu S1 und S2
gezeigt. Wenn wir zur Angabe dieser euklidischen Abstände Betrag-Striche benutzen, ergibt
den hyperbolische Abstand von RP2 und RP1.

In den letzten drei Teilen der Animation wird der Raumpunkt RP2 durch einen Raumpunkt RP3 auf der blauen
Geraden h ersetzt, die wir 'polar' zu g nennen. h schneidet wie auch g die Zentrale und zwar so, dass der
Mittelpunkt M der Schnittpunkte C* bzw. C auf Par liegt und g und h parallel zur Tangential-Ebene von M
an Par sind. Die Bilder von g und h bei der Projektion parallel zur z-Achse auf die x-y-Ebene sind euklidisch
orthogonal. Die beiden Tangential-Ebenen an Par durch h berühren Par in den Punkten S1 und S2 auf g. Die
Tangenten C*S1 und C*S2 an Par sowie die tangentialen Verbindungen von RP3 mit S1 und S2 sind blau
eingezeichnet.

Im ersten Bild des vierten Teils der Animation wird gezeigt, dass die Kreise K3 zu RP3 und K1 orthogonal
sind. Die anschließende Bewegung von RP3 auf h ändert daran nichts. K3 inzidiert in jeder Position von RP3
auf h mit den Punkten in der x-y-Ebene, die zu S1 und S2 auf Par gehören.

Wenn im fünften Teil RP1 auf g bewegt wird, bleibt die Orthogonalität erhalten, solange K1 reell ist. Daraus folgt,
dass das Bild von h bei Projektion parallel zur z-Achse auf die x-y-Ebene Potenz-Gerade aller reellen Kreise zu
Raum-Punkten auf g ist. Wenn RP1 sich dagegen unterhalb von Par befindet, ist der zugehörige imaginäre Kreis
nicht orthogonal zu K3, schneidet K3 aber auf einem Durchmesser von K1.

Im letzten Teil der Animation wird der fünfte Teil umgekehrt durchlaufen, aber dabei RP1 durch Anti-RP1 ersetzt.

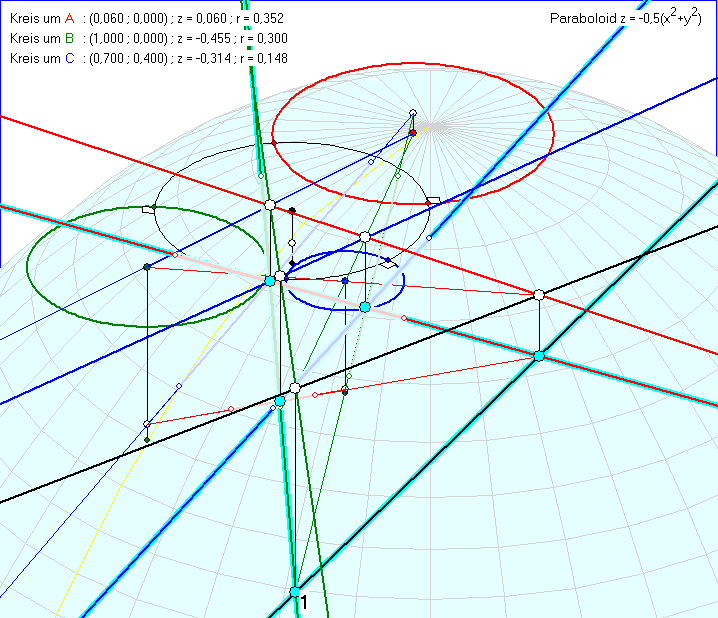
Diese Animation veranschaulicht den folgenden 'Gleichheits-Achsen'-Satz:

Gegeben seien drei reelle Kreise KA, KB und KC zu den Raum-Punkten mit den Quadrupeln a, b und c.
KI bzw. KJ sei ein Kreis mit der Eigenschaft, dass die Inversion oder Anti-Inversion an KI bzw.
KJ den Kreis KC in KB bzw. KA abbildet. g sei die Gerade durch die Raum-Punkte RI und RJ.
Dann hat die zu g polare Achse h die folgende Eigenschaft:
Für alle Raum-Punkte RP auf h mit dem Tripel p gilt.
Wenn KP mit dem Kreis KC einen Winkel der Größe bildet, dann hat KC mit KB und KA einen
Winkel der Größe oder . Im Fall, dass KP mit KC keinen gemeinsamen Punkt hat, schneiden
sich auch KP und KA sowie KP und KB nicht und die Abstände zu KA, KB und KC sind gleich.

Das erste Bild der Animation zeigt zu den drei Kreisen in der x-y-Ebene die hellblau unterlegte Gerade g und
die gelb unterlegte Gerade h. g ist die Verbindungs-Gerade der Raum-Punkte RI und RJ, deren zugehöriger
roter bzw. grüner Kreis KI bzw. KJ der im Satz genannte Inversions-Kreise ist. Ein dritter (blauer) Inversions-
Kreis zum Raum-Punkt RL hat mit KI und KJ zwei Punkte gemeinsam. Sein nicht sichtbarer Raum-Punkt
inzidiert mit g. Jeder der Zentren von KI, KJ und KL ist Ähnlichkeits-Zentrum vom Paar zweier Kreise von
KI, KJ und KL, deren Farbe nicht rot bzw. nicht grün bzw. nicht blau ist. Die Zentren von KI, KJ und KL
inzidieren also in der x-y-Ebene mit einer Ähnlichkeits-Achse des Tripels der drei Kreise und g ist die
zugehörige Raum-Gerade. Wir nennen sie deshalb 'Raum-Ähnlichkeits-Achse'
( im Bild unten auch kurz 'Ähnlichkeits-Achse').
.
Im ersten Bild der Animation hat der gelb unterlegte Kreis zum Raum-Punkt P auf h den Mittelpunkt im Radikal-
Zentrum von KA, KB und KC. Er schneidet die drei Kreise euklidisch orthogonal schneidet. Im ersten Teil der
Animation wandert RP auf h weiter bis KP alle drei Kreise berührt. Auf dem Weg dorthin werden die Winkel
mit KA, KB und KC im gleichen Maß größer, die mit KI, KJ und KL bleiben aber 90°. Am Ziel wird der
magenta-farbene Berühr-Kreis KM1 abgelegt. Dabei zeigt sich, dass jeder Berührpunkt von KM1 auf dem
Kreis durch die gemeinsamen Schnittpunkte von KI, KJ und KL liegt, der orthogonal zu dem berührten Kreis
und dem Radikal-Kreis ist.

Bei der weiteren Bewegung von RP in gleicher Richtung auf h gibt es keinen Schnitt-Winkel mit KA, KB und
KC mehr, die unten angezeigten Abständes sind aber für alle drei Kreise gleich. Wenn dabei RP in das Innere
des Paraboloids eintritt, wird KP imaginär und zur Abstands-Berechnung wird statt der Arccosh-Funktion
die Arcsinh-Funktion benutzt. Beim anschließenden Rückweg geht RP zunächst bis zum Radikal-Zentrum
zurück. Dann werden die Schnittwinkel mit KA, KB und KC eingezeichnet und der Weg bei abnehmen dem
Winkel bis zur Größe Nullfortgesetzt. KP berührt dann KA, KB und KC im zweiten Schnittpunkt der Lot-
Kreise und wird zum Berühr-Kreis KM2. Auch beim Fortsetzen des Wegs in gleicher Richtung und dann
zurück stimmen die Abstände oder Winkel von KP zu KA, KB und KC überein. Im letzten Bild wird gezeigt,
dass die Berühr-Punkte von KA, KB und KC mit KM1 und KM2 kollinear mit dem Radikal-Zentrum sind.

Vergleiche dazu die letzten beiden Bild-Folgen auf der Seite Kreise auf der Kugel >' Dreiseite ohne Ecken'.



.

In dieser Animation werden die gleichen Kreise KA, KB und KC wie in der vorherigen Animation
betrachtet, aber der grüne Inversions-Kreis KJ wird durch den Anti-Inversions-Kreis KJ* ersetzt,
der KC in KA spiegelt. Das Zentrum J* von KJ* in der x-y-Ebene ist jetzt nicht mehr äußeres
Ähnlichkeits-Zentrum wie in der vorigen Animation, sondern inneres. Es gibt also noch immer zwei
gemeinsame Tangenten von KC und KA durch den grünen Mittelpunkt, aber dieser liegt jetzt zwischen
KC und KA. Die Raum-Ähnlichkeits-Achse durch KI und KJ* sei g1 genannt und die dazu polare
Raum-Gerade h1. Sie sind auch hier hellblau bzw. gelb unterlegt. Mit g1 inzidiert ein drittes Raum-
Ähnlichkeits-Zentrum, das aber hier zu einem Anti-Inversions-Kreis KL* gehört. Die drei Kreise KI,
KJ* und KL* haben hier keinen gemeinsamen Punkt.

Im ersten Bild der Animation ist der Kreis KP zum Raum-Punkt KP auf h1 auch hier der Radikal-Kreis von
KA, KB und KC. Er schneidet KA, KB und KC und auch KI euklidisch orthogonal, nicht aber KJ* und
KL*. Diese schneidet KP in einem Durchmesser.

Auch in dieser Animation wandert RP auf h1 hin und her, wobei die Maß-Zahlen mit KA, KB und KC
übereinstimmen. Dabei werden wieder zwei Berühr-Kreise abgelegt. Ihre Berühr-Punkte haben hier nicht
wie in der vorherigen Animation eine Verbindung mit einem Kreis aus einem Kreis-Büschel, aber auch
hier eine geradlinige Verbindung mit dem Radikal-Zentrum. Diese ist im letzten Bild der Animation
eingezeichnet. Sie inzidiert mit dem Pol der Gleichheits-Achse in der xy-Ebene bezüglich KA bzw. KB
bzw. KC . Zur Erläuterung siehe die Seite Kreise auf der Kugel > ' Dreiseite ohne Ecken'.

Das erste Bild dieser Gleitschau zeigt das vollständige Vierseit aus Ähnlichkeits-Achsen mit
den Ähnlichkeits-Zentren zu den drei Kreisen KA, KB und KC als große weiße Punkte
und die zugehörigen Raum-Ähnlichkeits-Zentren als große hellblaue Punkte zusammen mit
den hellblau unterlegten Raum-Ähnlichkeits-Achsen. Nur jeweils fünf der sechs Punkte sind
zu sehen. Im zweiten Bild sind die zu den Raum-Ähnlichkeits-Achse zugehörigen polaren
Geraden zugefügt, die wir Gleichheits-Achsen nennen. Diese gelb unterlegten Geraden
haben den Raum-Punkt des Radikal-Zentrums gemeinsam. Er ist der Pol der Ebene E in der
die Raum-Ähnlichkeits-Achsen liegen. Alle Tangential-Ebenen in Punkten der Schnitt-Kurve
von E mit Par inzidieren also mit diesem Pol. Das dritte Bild zeigt die Geraden aus der
Vogel-Perspektive.

Im vierten und fünften Bild werden alle acht Berühr-Kreise von KA, KB und KC gezeigt.

Zur Berechnung von Geraden, die zueinander polar sind:

Wir legen hier die Bilinearform zu Grunde, der bei der
Darstellung der Kreis-Geometrie über die stereographische Projektion von Kreisen auf der Kugel in
den vorangehenden Seiten die Form entspricht, die auch in
der speziellen Relativitäts-Theorie benutzt wird. Zwei Geraden sind dort zueinander polar, wenn ihre
Richtungs-Vektoren euklidisch orthogonal sind und das Produkt ihrer Abstände vom Einheits-Kugel-
Zentrum gleich 1 ist. Wenn die Kugel durch das Paraboloid Par mit der Gleichung
ersetzt wird, übernimmt die Projektion parallel zur z-Achse auf die x-y-Ebene die Rolle der
stereographischen Projektion. Die Bilder zueinander polarer Geraden g und h sind dann euklidisch
orthogonal und die Zentrale durch den Schnittpunkt der Bilder parallel zur z-Achse trifft g und h in
Punkten, deren Mittelpunkt auf Par liegt.

M sei die am Schluss der vorangehenden Seite 'Inversion und Anti-Inversion' definierte Maß-Matrix M zu f.
Wenn D und E zwei Ebenen durch g sind, dann verbindet die dazu polare Gerade h die Pole von D und E.
Deren Quadrupel sind d.M und e.M. Wenn P und Q verschiedene Punkte auf g sind, dann ist h die Schnitt-
Gerade der dazu polaren Ebenen mit den Quadrupeln p.M und q.M. Wenn g durch ein Tripel-Paar
in Plücker-Koordinaten gegeben ist, dann hat h das Tripel-Paar
. Dabei gibt das ersten Tripel u einen Richtungs-Vektor von g an und
den Orts-Vektor vom Fußpunkt des Lots vom Ursprung auf g. Die Zentrale von g und h,
die beide Geraden trifft und parallel zur z-Achse verläuft, schneidet die x-y-Ebene im Punkt mit dem Tripel
. Die Ebene durch g oder h parallel zu z-Achse schneidet Par in
einer Parabel, deren Scheitel-Punkt auf der Zentralen liegt.

Zu Plücker-Koordinaten siehe auch die Pdf-Datei 'Geraden und Gewinde im dreidimensionalen projektiv
-metrischen Raum' (--> https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf ).

Zur Begründung des Gleichheits-Achsen-Satzes:

Wir gehen von drei reellen Kreisen KA, KB und KC zu den Raum-Punkten mit den f-normierten Quadrupeln
a, b und c aus. Da die Kreise reell sind, gilt also f(a;a) = f(b;b) = f(c;c) = 1. Die in dem Gleichheits-Achsen-
Satz genannten Kreise KI und KJ haben dann nach den Erklärungen am Schluss der Seite 'Inversion und Anti-
Inversion' die Raumpunkte RI und RJ mit den Quadrupeln und , wobei das Minus-Zeichen im Fall
der Inversion und das Plus-Zeichen im Fall der Anti-Inversion gilt. Im ersten Fall ist der Mittelpunkt von KI bzw.
KJ also ein äußeres Ähnlichkeits-Zentrum und im zweiten Fall ein inneres. g ist die Raum-Ähnlichkeits-Achse
durch RI und RJ. Die dazu polare Gerade h ist dann die Schnitt-Gerade der zu RI und RJ polaren Ebenen mit
den Quadrupeln bzw. . Für einen Punkt P auf h mit dem f-normierten Quadrupel p gilt dann
, wobei das hochgestellte T die Umwandlung der Zeile p in eine
Spalte bewirkt. Daraus folgt und auch , da a, c und p f-normiert sind.
Analog ergibt sich .

Zur Berechnung eines Punktes P auf einer Gleichheits-Achse h, für den gilt:

Wir gehen davon aus, dass f(a;a) = 1 und h durch zwei verschiedene Punkte Q und R auf h gegeben ist.
Dann gibt es reelle Zahlen s und mit .
Aus folgt und daraus wegen f(a;a) = 1
und
Wenn wir die
erste, zweite bzw. dritte Klammer mit u, v bzw. w bezeichnen, ergibt sich für die quadratische Gleicung mit
s = 1 für t das Lösung-Paar . Für k = 0 fallen die Lösungen zusammen. P ist dann das
Radikal-Zentrum von KA, KB und KC und der Schnittwinkel von KP mit KA, KB und KC. hat die
Größe 90°. Für k = 1 ergeben sich die Raum-Punkte für die beiden zu h gehörigen Berühr-Kreise.


.

Zur algebraischen Lösung des apollonischen Kreis-Problems:

Wir gehen von drei reellen Kreisen KA, KB und KC zu den Raum-Punkten (xa;ya;za), (xb;yb;zb) und
(xc;yc;zc) aus, die keine Null-Kreise sind. Ihre Radien ra, rb und rc sind dann reell und positiv. Wir
unterscheiden bei den Kreisen zwei verschiedene Orientierungen: eine positive und eine negative, die bei
Sicht auf die xy-Ebene von Punkten der positiven z-Achse zu einer Links- bzw. Rechts-Drehung gehört.
Man kann sich diese Orientierung mit Hilfe von Geschwindigkeits-Vektoren vorstellen, die tangential an die
Punkte der Kreise angeheftet sind. Erst durch Einführung einer Orientierung ist es möglich, bei Kreisen mit
gemeinsamen Punkten die Schnittwinkel-Größen und zu unterscheiden. Wenn sich orientierte
Kreise berühren, ist die Schnittwinkel-Größe 0°, wenn die Kreise im Berühr-Punkt die gleiche Richtung
haben und 180° bei entgegengesetzter Richtung.

Die Orientierung eines Kreises KX legen wir durch das Vorzeichen der 'Krümmung' fest.
wobei rx > 0 vorausgesetzt wird. Bei positiver Orientierung und Krümmung mit Geschwindigkeits-
Vektoren, die in Richtung einer Links-Drehung zeigen wird als 'Inneres' des Kreises die von KX
umschlossene Punktmenge mit dem Mittelpunkt ohne die Punkte auf KX angesehen, bei negativer
Krümmung ist das Innere des Kreises in dieser Bezeichnungsweise die Menge der Punkte, die nicht
von KX umschlossen werden und auch nicht auf KX liegen (im Unterschied zum umgangssprachlichen
Gebrauch). Wenn sich zwei Kreise KX1 und KX2 von außen berühren, ist die Schnittmenge des
Inneren von KX1 und des Inneren von KX2 leer.


Das Quadrupel (xa;ya;za;1) des Raumpunktes von zum Beispiel KA wird f-normiert durch Division
mit . Dann ist f-normiert mit f(pa;pa) = 1
auch wenn ka negativ ist. Bei einem imaginären Kreis würde sich -1 ergeben. Ein reeller Kreis KM1
mit dem entsprechend normierten Quadrupel berührt
KA bei gleicher Orientierung genau dann von außen bzw. innen, wenn gleich
-1 = cos(180°) bzw. 1 = cos(0°) ist. Dabei ist 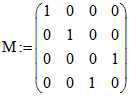die am Schluss der Seite ' Inversion
und Anti-Inversion' eingeführte Maß-Matrix, die zur Maß-Funktion f gehört. Wenn KD alle drei Kreise
KA, KB und KC bei gleicher Orientierung der vier Kreise von außen berühren soll, muss für die Matrix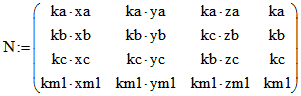
mit den Zeilen pa, pb, pc und pm1 gelten:
mit 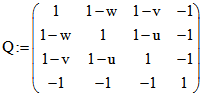und u := 1 - f(pb;pc), v := 1 - f(pc;pa)
und w := 1 - f(pa;pb). ist wegen äquivalent mit
und mit . Die letzte Zeile (0;0;1;0) von M stimmt mit
der letzten Zeile vonüberein, deren Terme die Komponenten von pm1
als Unbekannte enthält. Dabei ist die Gleichung



quadratisch in km1 und enthält xm1, ym1 und zm1 nicht. Die beiden Lösungen dieser Gleichung
geben die Krümmungen von Berühr-Kreisen an, dessen Raum-Punkte auf der gleichen Gleichheits-
Achse liegen. Die Gleichung ist linear in xm1 und enthält ym1 und zm1 nicht. Die Gleichung
ist linear in ym1 und enthält xm1 und zm1 nicht und die Gleichung ist linear in zm1
und enthält xm1 und ym1 nicht.


.