Es lebe die Geometrie!

Höhen im 6-Rechteck

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum I'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum II'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_II.pdf

Unter einem 6-Rechteck verstehen wir ein 6-Eck im dreidimensionalen euklidischen affinen Raum, bei dem
alle Ecken-Winkel die Winkelgröße 90° haben und keine vier aufeinander Eckpunkte komplanar sind, also
in einer gemeinsamen Ebene liegen. Wenn man von drei paarweise nicht komplanaren Geraden g, h und
j ausgeht, dann bilden die Fußpunkte der Lotgeraden zu den Paaren g, h und h, j und j, g ein 6-Rechteck.
Die Lotgerade von z.B. g, h ist die eindeutig bestimmte Gerade a, die g und h beide rechtwinklig schneidet,
und die Schnittpunkte sind die zugehörigen Fußpunkte. In der Geometrie der Raumgeraden spielen die
Lotgeraden eine ähnliche Rolle wie die Verbindungsgeraden zweier Punkte in der zweidimensionalen
Geometrie. Diese Analogie wird in den folgenden Zeichnungen genutzt, um in dem Geraden-Gewirr die
Übersicht zu behalten. Gegeben ist dabei ein 6-Rechteck ABCDEF, bei dem die Kantengeraden AB, CD und
EF den Eck-Punkten des Dreiecks unten rechts im Bild entsprechen, die hellrot wie A bzw. hellblau wie C
bzw. hellgrün wie E gezeichnet sind. Diese Farben werden auch für die Strecken AB, CD und EF benutzt.
Dagegen wählen wir für die Strecken BC , DE und FA die Farben dunkelgrün, dunkelrot bzw. dunkelblau.
Diese Farben verwenden wir auch für die Seiten des Analogie-Dreiecks unten recht in den Bildern.

Die Analogie des 6-Rechtecks mit einem Dreieck zeigt sich auch bei Betrachtung der Spiegelungen an den
Kantengeraden von ABCDEF und der Spiegelungen an den Eckpunkten und Seitengeraden des Dreiecks.
Denn ein Eckpunkt dieses Dreiecks liegt genau dann auf einer seiner Seitengeraden, wenn die zugehörigen
Spiegelungen vertauschbar sind, also die Hintereinanderschaltung der beiden Spiegelungen sich bei
getauschter Reihenfolge nicht ändert. Entsprechend sind die Spiegelungen an Kantengeraden von ABCDEF
genau dann vertauschbar, wenn diese Geraden sich senkrecht schneiden.

Das in dieser Animation dargestellte 6-Rechteck ABCDEF entsteht dadurch, dass an das grau gezeichnete
Basis-Dreieck ACE drei rechtwinklige gelbe Dreiecke angesetzt wurden, so dass nicht nur die Winkelgrößen
bei B, D und F, sondern auch bei A, C und E 90° betragen. Das Basis-Dreieck hat drei Seiten mit den
Längen und liegt in der xy-Ebene mit dem Schwerpunkt im Koordinaten-Ursprung (siehe das erste Bild
der Gleitschau nach der Animation). Dabei muss das Dreieck ABC mit dem Basis-Dreieck einen Winkel
zwischen den Grenzen und einschließen. Die Winkel der
anderen beiden gelben Dreiecke gegenüber dem Basis-Dreieck sind dann eindeutig bestimmt. Wenn dabei
kleinergleich ist, haben alle Seiten die Länge 1, andernfalls nur die Kanten
AB, BC, CD und DE, während EF größer als 1 ist und FA kleiner als 1, im Grenzfall sogar 0. Beim einem
der beiden Grenzwinkel oder bei den Winkelgrößen , also ungefähr 125,3° und 234,7°,
bildet das 6-Rechteck einen Kantenzug in einem Würfel. Um dies deutlich zu machen, wurden die Dreiecke
BCD und EFA durch vierte Parallelogrammpunkte ergänzt.

Im Bild oben links sind Punkte und Großkreise einer Kugel vom Radius 1 dargestellt (in einem anderen
Maßstab), die zu den Richtungs-Vektoren der Kanten AB, BC, CD, DE, EF und FA gehören, deren Länge
zu 1 normiert wurden. Dabei sind die blass gezeichneten Vektoren AB, CD, EF Ortsvektoren von Punkten,
die zusammen mit ihren ebenfalls eingezeichneten Antipoden den Eck-Punkten des Analogie-Dreiecks unten
rechts entsprechen. Die in kräftige Farben dargestellten Vektoren sind Normalen-Vektoren von Großkreisen;
sie sind also orthogonal zu den Ebenen der Großkreise. Diese Kreise entsprechen den Seiten-Geraden im
Analogie-Dreieck. Denn jedes Antipoden-Paar ist das Paar der Schnittpunkte von zwei der drei Kreisen.
Darum ist zum Beispiel der hellblaue Vektor zu CD orthogonal zu dem dunkelgrünen und dem dunkelroten
Vektor zu BC bzw. DE. In dem zweiten Standbild der Gleitschau ist markiert, welche Vektoren aufeinander
senkrecht stehen. Die Punkte zu den blassen Vektoren sind durch dick gezeichnete Kreisbögen verbunden.
Wir nennen dieses Bild 'Kugel-Bild des 6-Rechtecks'. Die Geometrie der Antipoden-Paare und Großkreise
auf der Kugel wird als 'elliptische Geometrie' bezeichnet. Dabei bezieht sich das Adjektiv 'elliptisch' nicht auf
die Projektions-Darstellung der Großkreise durch Ellipsen, sondern ergab sich in der Geschichte der
Mathematik aus dem Gegensatz zur hyperbolischen Geometrie.

In dieser Animation sind zu 6-Rechteck ABCDEF Strecken zu Geraden hinzugefügt worden, die in dem
Analogie-Dreieck unten rechts den Höhen-Geraden und dem Orthozentrum entsprechen, in dem sich die
Höhen schneiden. Der Höhe senkrecht zur roten Seite entspricht beim 6-Rechteck die hellrote Strecke,
die senkrecht auf der Kante DE steht und auch auf der Kante AB, da die Inzidenz einer Gerade mit einem
Punkt der Dreiecks-Ebene der Orthogonalität bei Raumgeraden entspricht. Die Raumgerade, die orthogonal
zu DE und AB ist, bezeichnen wir als 'Höhenlot zu DE und AB '. Die Animation zeigt, dass die drei
Höhenlote des 6-Rechtecks ein gemeinsames Lot haben, das wir 'Höhen-Achse von ABCDEF ' nennen.
In der Animation liegt die violette Strecke auf dieser Höhen-Achse, die dem Orthozentrum im Analogie-
Dreieck entspricht. Dass es in jedem 6-Rechteck diese Gerade gibt, die senkrecht zu den drei Höhen-Loten
steht, ist die Aussage des Satzes von Hjelmslev(1873-1950) und Morley(1860-1937).
In Kugel-Bild gilt entsprechend der Höhen-Satz der elliptischen Geometrie.

Siehe dazu auch den oben auf dieser Seite angegebenen Pdf-Text

Hier wird der Winkel zwischen den Dreieck ABC und dem Basis-Dreieck ACE im Intervall
variiert. Für
haben dann die Kanten EF und FA nicht mehr die Länge 1, wie die übrigen Seiten. An der Existenz der
Höhen-Achse ändert sich aber nichts.

Zur Berechnung der euklidischen Achse zweier Raumgeraden:

Wir rechnen zunächst im dreidimensionalen affinen Raum mit reellen Zahlen als Koordinaten. Strecken und
Winkel werden dabei wie üblich mit dem inneren Produkt für Vektoren
und berechnet. Wenn u und v Ortsvektoren von Raumpunkten sind, ist
die Länge der Strecke zwischen diesen Punkten also durch gegeben. Für den Winkel
zwischen Schenkeln mit Richtungsvektoren u und v der Länge 1 ist der Kosinus der Winkelgröße.

Unter der 'euklidischen Achse' zweier nicht paralleler Raumgeraden g und h verstehen wir die eindeutig
bestimmte Gerade j, die g und h beide orthogonal schneidet. Eine gemeinsame Lotgerade j gibt es auch
dann, wenn g und h parallel sind, sie ist dann aber nicht eindeutig bestimmt, da mit j auch jede g schneidende
Parallele zu j gemeinsame Lotgerade ist, denn sie schneidet auch h. Zu beachten ist dabei, dass wir nur dann
die Bezeichnung 'Achse' verwenden, wenn diese g und h orthogonal trifft und eindeutig ist. Falls nicht parallele
Geraden g und h komplanar sind, also in einer Ebene E liegen, ist die Achse von g und h die Gerade durch
den Schnittpunkt von g und h, die orthogonal zu E ist.

Die Achsen-Berechnung wird dadurch vereinfacht, dass man jede Raumgerade h durch ein Tripel-Paar
(u;v) angibt, wobei u ein Richtungs-Vektor der euklidischen Länge 1 von h ist und v das Kreuz-Produkt
aus dem Orts-Vektor p eines Punktes P auf h
und dem Richtungs-Vektor. Wir kürzen (u;v) durch ein fettes u ab. u und v sind orthogonal, da das innere
Produkt der beiden Vektoren gleich Null ist. Der Fußpunkt des Lots vom
Koordinaten-Ursprung auf h hat den Ortsvektor . Wenn man u als Richtungs-Vektor einer Kraft deutet,
die an einem Punkt auf h angreift, ist v das Drehmoment bezogen auf eine Achse durch den Ursprung, die
senkrecht auf der Ebene durch den Ursprung und h steht.

Man nennt die sechs Koordinaten von u und v auch 'Plücker-Koordinaten' nach Julius Plücker(1801-1868).

Die Eigenschaft 'orthogonal' für ein Paar (g ; h) von Raumgeraden kann man in zwei Aspekte zerlegen. Denn
g und h mit den Tripel-Paaren s = (s;t) und u = (u;v) sind genau dann orthogonal, wenn ihre Richtungs-
Vektoren orthogonal sind und sie außerdem einen gemeinsamen Punkt tragen. Diese zweite Eigenschaft ist
genau dann erfüllt, wenn gleich Null ist. Wir erweitern darum die Verknüpfung auf Tripel-Paare
durch die Definition . g und h sind also genau dann orthogonal, wenn
gilt. Eine Gerade j mit dem Tripel-Paar m ist genau dann Achse von g und h, wenn gilt.
Nur wenn dabei g und h nicht parallel sind, nennen wir j 'Achse'.

Aus folgt, dass u nur dann das Tripel-Paar einer Geraden
ist, wenn die zweite Komponente von gleich Null ist.

Zur Berechnung der eindeutig bestimmten Achse zu nicht parallelen Raumgeraden g und h erweitert man das
Kreuz-Produkt auf Tripel-Paare durch die Definition . Für ,
und ist dann zwar und , aber ist nur dann das
Tripel-Paar einer Geraden, wenn g und h einen Schnittpunkt haben oder ihre Richtungsvektoren orthogonal
sind. Andernfalls sind nämlich die beiden Tripel von nicht orthogonal. Wir bezeichnen dann m als Tripel-
Paar eines 'Gewindes'. In dem Fall ist das Tripel-Paar der Achse von g und h durch
bestimmt. Diese Umwandlung eines Tripel-Paars zu einem Gewinde in ein Tripel-Paar zu einer Geraden
funktioniert auch dann, wenn m und n nicht über ein Kreuz-Produkt bestimmt wurden. Man muss dann jedoch
eventuell beide Tripel durch die Länge des Vektors m teilen, bevor man die Formel
anwendet.

Auf den folgenden Seiten werden die Raumgeraden zum Teil mit einer Orientierung versehen. Sie ergibt sich
für eine Gerade h mit dem Tripel-Paar u = (u ; v) daraus, dass man die Tripel-Paare u und -u = (-u ; -v)
unterscheidet, die h mit entgegengesetzten Richtungs-Vektoren beschreiben. Bei einer nicht orientierten
Gerade g sind u und -u beide Tripel von g. Sie sind beide normiert, falls u die Länge 1 hat.

Falls g und h parallel, aber verschieden sind, ist der Null-Vektor (0;0;0), den wir verkürzt auch mit 0
bezeichnen. Da dieser Vektor keine Richtung angibt, ist nicht das Tripel-Paar einer
Geraden im affinen Raum. Man kann aber diesem Tripel-Paar in einer Erweiterung des affinen Raums zu
einem projektiven Raum eine 'unendlich ferne Gerade' zuordnen, die wir hier aber nicht 'Achse' nennen.

Ein weiterer Aspekt der Achsen-Berechnung ergibt sich aus einer Idee von Eduard Study (1862-1930).
Study beschrieb das Tripel-Paar mit Hilfe des willkürlich gewählten Symbols
durch das Tripel . Mit den Komponenten dieses Tripels
wird zunächst wie in der üblichen reellen Algebra gerechnet; wenn sich darin aber ein Term ergibt,
wird an diese Stelle Null eingesetzt. Einen Term der Form mit reellen Zahlen x und y nennt man
'duale Zahl' . spielt dabei eine entsprechende Rolle wie die imaginäre Einheit i bei komplexen Zahlen.
In dem Term nennen wir x den 'Reatteil' und y den 'Dualteil' der dualen Zahl.

Die Definitionen der Verknüpfungen und für Tripel dualer Zahlen ergeben sich in naheliegender Weise
aus der für reelle Zahlen. wird zur Dualzahl .
Analog gehen wir beim Kreuz-Produkt vor, wie man in folgenden Beispielen sieht.

Beispiele :

Im Fall existiert also eine duale Zahl , nämlich , andernfalls
kann man aber durch nicht teilen. Der Kehrwert von ist also
.















Für Tripel reeller Zahlen und , errechnet man
.

Man kann also ein Gewinde-Tripel aus dualen Zahlen durch Multiplikation mit der invertierbaren
dualen Zahl in ein Geraden-Tripel verwandeln. Jedes Dualzahl-Tripel in der Menge
gehört zu einem Gewinde oder einer Geraden. In der
Menge dieser Gewinde oder Geraden gibt es nur eine einzige Gerade, die wir auch als Achse der
Gewinde dieser Menge bezeichnen. Für ein Tripel a dieser Geraden ist der Dualteil von gleich
Null. a' ist nur dann ebenfalls ein Tripel dieser Geraden, wenn a' aus a durch Multiplikation mit einer
reellen Zahl x (ungleich Null) entsteht.

Aus und folgt . Daran sieht
man die Gleichartigkeit der Berechnungen zu Raumgeraden und zur Geometrie auf der Kugelfläche. Diese
Gleichartigkeit kann durch das Kugelbild in den Animationen nur verkürzt dargestellt werden, weil dafür
nur die Reatteile der dualen Zahlen benutzt werden, also bei nur das Tripel m aus reellen Zahlen.
Wenn man auch die Dualteile berücksichtigt, zeigt sich die Isomorphie der Geometrie der Geraden im
dreidimensionalen euklidischen Raum zur zweidimensionalen elliptischen Geometrie mit dualen Zahlen
als Koordinaten.

Durch Nutzung der dualen Zahlen ergibt sich eine einfache Formel zur Berechnung des Tripel-Paars der
Höhen-Achse im 6-Rechteck ABCDEF. Sei s bzw. u bzw. w das Tripel aus dualen Zahlen, das sich, wie
oben dargestellt, aus dem Tripel-Paar der Kanten-Gerade zu BC bzw. DE bzw. FA ergibt. Dann bestimmt
ein Gewinde, dessen Achse die gewünschte Höhen-Achse ist.

Wenn wir im Folgenden die Bezeichnung ' d-normierter Term zum Dualzahl-Tripel '
verwenden, meinen wir damit den Term, der aus in zwei Schritten entsteht:

1. Wenn die Länge r des Vektors m nicht 1 ist, werden die Vektoren m und n durch diese Länge geteilt.
2. Wenn das Ergebnis dieser Teilung ist, stellt den d-normierten Term
zu dar. Dieses Ergebnis ergibt sich auch durch Multiplikation des Duakzahl-Tripels mit
der Dualzahl .
Der Realteil und der Dualteil des sich so ergebenden Dualzahl-Tripels bilden das Tripel-Paar der zu
gehörigen Gerade. Das innere Produkt dieses Dualzahl-Tripels mit sich selbst ist .

Manchmal ist es nützlich, den d-normierten Term in anderer Weise darzustellen. Dazu definieren wir:

Der Betrag einer dualen Zahl ist die gleiche Zahl, wenn die reelle Zahl x nicht negativ ist,
andernfalls ist der Betrag gleich . Wir nennen positiv bzw. negativ, wenn
x posiriv bzw. negativ ist. bedeutet x = 0 und y = 0.

Die Wurzel aus der positiven dualen Zahl ist . Denn
.

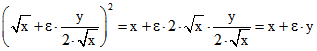Damit ergibt sich als d-normierter Term zu .
Denn mit der positiven reellen Zahl errechnet man:

und .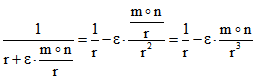

d-normierbar sind genau die Tripel-Paare m, für die der Realteil von ungleich Null ist. Darum ist das
Kreuzprodukt der Dualzahl-Tripel zweier Raumgeraden genau dann d-normierbar, wenn sie nicht parallel
sind. Es gibt folglich genau dann dazu eine Achse.