Es lebe die Geometrie!

Die Rollgleitzahl

Die Rollgleitzahl gibt das Verhältnis der Geschwindigkeiten vom Kontaktpunkt zweier berührender
Zahnräder auf den beiden Zahnflanken an. Diese Zahl wird analog für beliebige Kurven definiert, die
berührend aneinander abrollen oder gleiten. Beim Rollen ohne Rutschen ist die Rollgleitzahl Eins,
z. B. wenn ein Kreis an einer Geraden abrollt. Bei Zahnrädern ist dies aber nur ausnahmsweise
der Fall.

Im Fölgenden betrachten wir die Rollgleitzahl eines Zahnrads bezüglich einer Zahnstange. Wenn man
diese Zahlen für zwei verschiedene Zahnräder bezüglich der gleichen Zahnstange bestimmt hat, ergibt
sich die Rollgleitzahl von Zahnrad 1 bezüglich Zahnrad 2 durch Quotienten-Bildung.

Die Animation zeigt den Zusammenhang zwischen den Geschwingigkeitsvektoren, die an den
Kontaktpunkt K angeheftet sind, wenn K die Kontaktkurve in Form einer '8' durchläuft. Hier gehört
die Kontaktkurve zu einer Zykloidenverzahnung, setzt sich also aus Kreisbögen zusammen. Der rot
berandete Pfeil gibt dabei die Geschwindigkeit von K auf der Kontaktkurve an. Wenn in K
ein Stift befestigt würde, der auf einer relativ zur Kontaktkurve nach rechts bewegten Zeichenebene
eine Spur zeichnen könnte, dann würde bei geeigneter Geschwindigkeit dieser Ebene die schwarze
Zahnstangenkurve entstehen. Diese Geschwindigkeit legt die Länge des schwarz berandeten Pfeils
fest, der mit der Richtung nach links an K geheftet ist. Nach dem Verzahnungsgesetz muss die
Vektorsumme senkrecht zu der Geraden durch K und den Wälzpunkt W in der Mitte der
Kontaktkurve stehen.

Die blauen Vektoren gehören zu der blauen Zahnrad-Kurve mit dem Mittelpunkt R (siehe Bild 1 der
Gleitschau). Der blaue Vektor senkrecht zur Geraden RK muss nach dem Verzahnungsgesetz so
lang sein, dass orthogonal zur Geraden WK ist.

Die Rollgleitzahl des Zahnrads bezüglich der Zahnstange im Kontaktpunkt K ist die reelle Zahl ,
für die gilt.

Zur Berechnung der Rollgleitzahl gehen wir vom Funktionenpaar (x(t) ; y(t)) zur Beschreibung der
Kontaktkurve mit einem Zeitparameter t aus. Für die Ableitungen gilt dann .
Es sei und r der Wälzkreisradius .
Dann ist der Vektor senkrecht zu und senkrecht zu .
Darum sind die zugehörigen Skalarprodukte gleich Null, also
und
.
Daraus folgt durch algebraische Umformung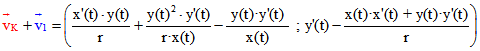
.
Durch den Grenzübergang ergibt sich daraus .
Wegen folgt .

In der Animation ist im 1. Teilstück (von W bis zum Eckpunkt A oben rechts) der Kontaktkurve
, wobei der Radius des 1. Teilstücks ist. Es folgt
. Die Rollgleitzahl ist also hier konstant. Das gilt auch für die anderen Teile der
Kontaktkurve. Dies wird in der Animation und den folgenden Bildern der Gleitschau in dem Grafen
glz(u) der Rollgleitzahlen in Abhängigkeit vom Parameter u erkennbar.

Die Animation zeigt die entsprechenden Bilder wie oben für die Evolventenverzahnung. Setzt man für
das erste Teilstück der Kontaktkurve , dann errechnet man .
glz(u) ist darum im Intervall [0 ; 1] linear. Dies gilt auch für die Intervalle [2 ; 4] und [5 ; 6].

In der Animation wird die Rollgleitzahl-Funktion für Kontaktkurven untersucht, die in den
Teilstücken 1, 3, 4 und 6 durch eine Potenzfunktion der Form mit n = 2, 3 und 10
gegeben sind. Setzt man so errechnet man .
Für t = 2 erhält man im Grafen glz(u) darum Parabel-Bögen. Für n = 3 und n = 10 hat der
Graf Polstellen bei u = 0, 3 und 6. In der Nähe dieser Stellen ist die Rollgleitzahl negativ. Dies
bedeutet, dass und entgegengesetzt gerichtet sind. Da der Betrag von
hier sehr klein ist, ist der Betrag von glz(u) sehr groß. Die Verzahnungskurve des Zahnrades hat
in dem dazu gehörigen Bereich Selbstüberschneidungen. Diese sind für n = 3 kaum erkennbar,
aber sehr deutlich für n = 10. Durch Erhöhung der Anzahl der Zähne des Zahnrads kann der
Bereich mit Selbstüberschneidungen verkleinert werden. Dies wird in den letzte Bildern der
Gleitschau dargestellt.