Es lebe die Geometrie!

Spiralen und Drehstreckungen

Die Spiralen dieser Seite sind näherungsweise Darstellungen von Fraktalen, die mit Hilfe zweier
Drehstreckungen und erzeugt werden. Ein derartiges Fraktal ist die kleinste abgeschlossene
Menge M von Punkten des , für die und gilt, so dass also jeder Punkt P in M
durch und in einen Punkt bzw. abgebildet wird, der ebenfalls in M liegt. (Wir schreiben
hier das Abbildungszeichen rechts hinter den abgebildeten Punkt.) Die Drehstreckungen haben hierbei
stets einen Streckungsfaktor kleiner als 1. Dies bedeutet, dass die Folge der Punkte bzw. , die
durch Hintereinanderschaltung von n gleichen Drehstreckungen entsteht, für n gegen Unendlich gegen
den Drehpunkt A bzw. B konvergiert, der Fixpunkt der Abbildung ist, also bei dieser Abbildung fest
bleibt. Da A und B also Häufungspunkte von M sind und M abgeschlossen ist, müssen sie Punkte von
M sein. Da M die kleinste unter und invariante Menge sein soll, besteht M aus allen Bildern von
A und B bei beliebig vielen Hintereinanderschaltungen von und in beliebiger Reihenfolge und Anzahl
(z.B. ). Daraus folgt, dass alle Punkte von M Häufungspunkte von M sind.

Graphische Darstellungen können (unter anderem wegen der Endlichkeit der Pixel) M nur annähernd
richtig wiedergeben. Man wendet dabei Hintereinanderschaltungen von und z.B. nur auf A an, weil
man dem Punkt B dann beliebig nahe kommt, wenn in der Hintereinanderschaltung genügend oft
vorkommt. Wenn man also alle Bildpunkte von A bei diesen Hintereinanderschaltungen zeichnet, erfasst
man mit Sicherheit Punkte in M und kommt dabei allen Punkten von M nahe. Aus einem entsprechenden
Grund kann man A durch irgendeinen anderen Punkt ersetzen. Dann sind aber die Bilder dieses Punktes
bei den ersten Hintereinanderschaltungen möglicherweise nicht Punkte von M. Darum zeichnet man die
Punkte erst dann, wenn in der Hintereianderschaltung genügend viele Exemplare von oder
vorkommen. In den unten folgenden Animationen wird der Punkt blau bzw. rot gezeichnet, wenn
die bei der Hintereinanderschaltung zuletzt angewandte Abbildung bzw. war.

Die Animation zeigt näherungsweise Darstellungen der Fraktale, die sich bei festgehaltenem
und einer Drehstreckung mit verändertem Drehwinkel ergeben. In dem 'Generator' oben
links werden die Daten dazu zeichnerisch angegeben. Der schwarze 'Startpfeil', der den Punkt
(0 ; 0) mit dem Punkt (1 ; 0) verbindet, wird durch bzw. in den blauen bzw. roten Pfeil
abgebildet. Wenn ein derartiger farbiger Pfeil einen Anfangspunkt (a ; b) mit dem Endpunkt
(a + c ; b + d) verbindet, der Pfeil also zum Verbindungsvektor (c ; d) gehört, dann ist die
zugehörige Drehstreckung durch die Abbildung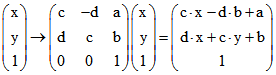
gegeben, wobei der Punkt (x ; y) in dieser 'projektiven Darstellung' durch die Spalte mit der dritten
Komponenten 1 beschrieben wird. (Für (c ; d) = (1 ; 0) ergibt sich eine Verschiebung, die meist
nicht als Drehstreckung bezeichnet wird.) In einer Darstellung mit komplexen Zahlen ist die Abbildung
durch gegeben mit , und . Wenn r die Länge des
Verbindungsvektors (c ; d) ist und w sein Richtungswinkel, dann gilt
.

Die in der Animation oben recht gezeigten Daten geben den Anfangspunkt (a ; b) der farbigen
Pfeile an und die Länge r und den Richtungswinkel w des Verbindungsvektors (c ; d) an.

Das zu den beiden Drehstreckungen gehörige Fraktal wird durch die Vereinigung M der blauen und
roten Pixel näherungsweise dargestellt. Die Menge der blauen bzw. roten Pixel allein ist eine Teilmenge
der zu M ähnlichen Menge bzw. . Wenn ein Punkt zu der Schnittmenge von und
gehört, dann kann die Farbe zufällig blau oder rot sein. In manchen Fällen ist diese Schnittmenge klein.
Dann ist die Menge der blauen bzw. roten Pixel allein eine gute Näherung für die zu M ähnliche Menge
bzw. . Wegen sind diese Mengen auch zueinander ähnlich.

In der Animation ergibt sich die Spiralstruktur von M auf Grund der Länge 0,959 (nahe bei 1) des
blauen Pfeils bei einem im Vergleich dazu kleinem roten Pfeil, wenn der Richtungswinkel w des blauen
Pfeils nahe bei liegt, wobei m und n kleine natürliche Zahlen sind. n gibt hierbei die Anzahl der
Arme der Spirale an.

Der mit einem weißen Rand markierte blaue bzw. rote Punkt in M ist der Fixpunkt von bzw. .
Beide Fixpunkte bleiben während der Animation unverändert.

In der auf die Animation folgende Gleitschau werden Standbilder der Animation gezeigt.

Die beiden Animationen zeigen den Übergang vom Fraktal M zu den dazu ähnlichen Teilmengen
und durch eine Folge von Drehstreckungen mit dem gleichen Drehpunkt, der zu bzw. gehört.
Damit soll die Bedeutung der 'Selbstähnlichkeit' des Fraktals klar gemacht werden. Wenn z. B. wie
oben in komplexer Form durch mit , und
gegeben ist, dann ist der Drehpunkt A durch bestimmt. Die Abbildung kann damit durch
beschrieben werden. Die Drehstreckungen, welche die Animation benutzt, um
Zwischenschritte zwischen M und zu zeigen, ergeben sich, wenn man hierbei den Richtungswinkel
w = 20° des blauen Pfeils durch einen Wert zwischen 0° und 20° ersetzt.


In dem ersten Bild der Gleitschau nach der Animation zur roten Teilmenge ist ein geometrischer Weg
zur Konstruktion des Fixpunktes gezeigt, wenn durch den Generator der schwarze Startpfeil und der
zur Drehstreckung gehörige farbige Pfeil gegeben ist: Man bestimmt den Schnittpunkt S der Geraden
durch die beiden Pfeile und dann die beiden Kreise durch S und die Anfangspunkte bzw. Spitzen der
Pfeile. Der Fixpunkt ist dann der zweite Schnittpunkt A der Kreise. Denn nach dem Umfangswinkelsatz
spannen dann A und die Pfeile Dreiecke mit gleichen Innenwinkeln auf.

In den beiden obenstehenden Animationen wird gezeigt, wie sich die Verschiebung der farbigen
Pfeile im Generator auswirkt. Der Anfangspunkt des blaue Pfeils wird am Rand eines Quadrats
herumgeführt und der rote am Rand eines Kreises. Dabei ergibt sich, dass die zugehörigen Fraktale
alle zueinander ähnlich sind. Die Fixpunkte von und sind hier durch eine gelbe Strecke verbunden.
Die Drehstreckung , welche die gelbe Strecke zum weiß verhüllten Ausgang-Fraktal M0 in die gelbe
Strecke zum in kräftigen Farben dargestellten Fraktal M1 abbildet, führt ganz M0 in M1 über, also
nicht nur die Fixpunkte darin. In der zweiten Animation mit der Verschiebung des roten Pfeils ist
eine Drehung, weil die gelben Strecken gleich lang sind.