Es lebe die Geometrie!

Evolventenverzahnung

Die Abschnitte der Kontaktkurve, auf denen der Wälzpunkt liegt, sind bei der Evolventenverzahnung
geradlinig. Dies ist die häufigste Art der Verzahnung bei Zahnrädern.

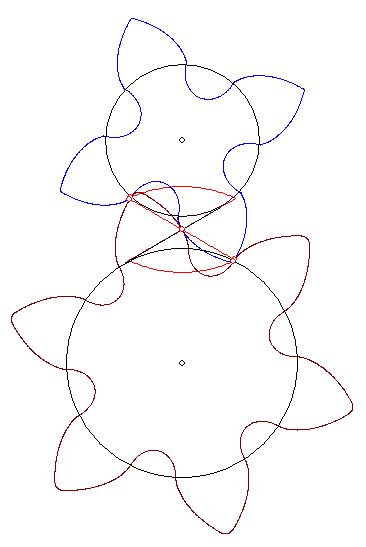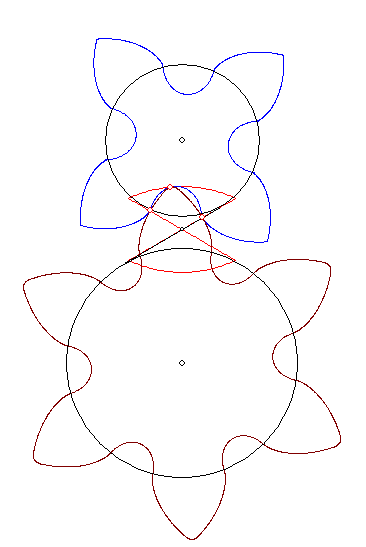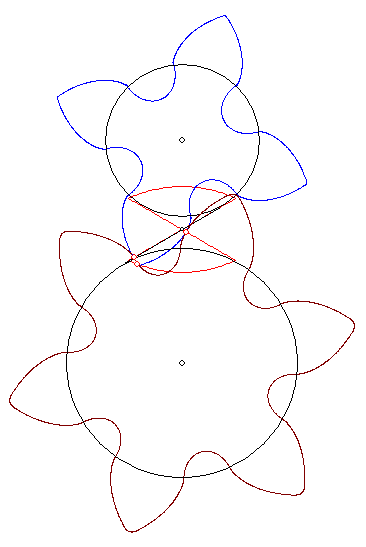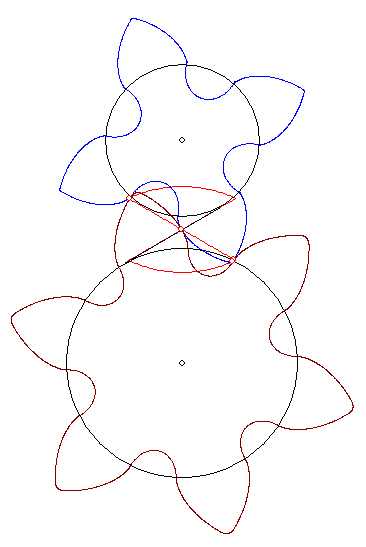
Zu den beiden Zahnrädern sind die 'Grundkreise' eingezeichnet. Die Evolventenverzahnung bewirkt eine
ähnliche Kraftübertragung wie ein Seil, das auf den Grundkreisen so aufgewickelt ist, dass es wie der
schwarze Strich in der Zeichnung durch den Wälzpunkt W in der Mitte des roten Kontaktkreises auf
der Geraden durch die Eckpunkte A oben rechts und C unten links verläuft. Falls das Seil nicht rutscht,
bewirkt dann eine Drehung des oberen Grundkreises gegen den Uhrzeigersinn eine Drehung des unteren
im Uhrzeigersinn. Wenn man das Seil bei feststehenden Grundkreisen im geradlinigen Teil durchschneidet
und die freien Enden straff hin-und herbewegt, dann liegen die beiden Enden auf zwei Kurven, bei denen
ein Teilstück mit den Zahnradflanken der Zahnräder übereinstimmt. Diese Kurven sind Evolventen der
Grundkreise. Die Radien der Grundkreise stehen in einem festen Verhältnis mit denen der Wälzkreise.
Wenn nämlich M der Drehpunkt eines der Zahnräder ist, dann ist der Radius r seines Wälzkreises die
Länge der Strecke MW und der Radius des zugehörigen Grundkreises gleich , wobei der
Steigungswinkel der Geraden CA ist.

Wenn der Abstand zweier Zahnräder mit Evolventenverzahnung geringfügig verändert wird, ändern sich
zwar die Radien der Wälzkreise, aber ihr Verhältnis bleibt gleich, da wegen der unveränderten Zahnflanken
die Grundkreisradien gleich bleiben. Dies ist neben der leichten Herstellbarkeit ein Grund dafür, dass diese
Verzahnungsart am häufigsten vorkommt.

Alle gezeichneten Zahnräder haben die gleichen Kontaktpunkt auf der roten Kontaktkurve. Diese
Punkte entsprechen den Schnittpunkten mit den Parallelen zur u-Achse in den s(u)-Graph oben links.
Die u-Werte 1, 2 , 4 und 5 gehören zu den Eckpunkte A (ober rechts), B (oben links), C (unten rechts)
und D (unten links). Die u-Werte 0, 3 und 6 gehören zum Wälzpunkt W.

Die Animation zeigt, wie auf Grund der Kontaktkurve und des s(u)-Graphen ein Zahnrad und die
zugehörige Zahnstange gezeichnet werden können. Bei Gültigkeit des Verzahnungsgesetzes ist der
s(u)-Graph eine Folge der Kontaktkurve.

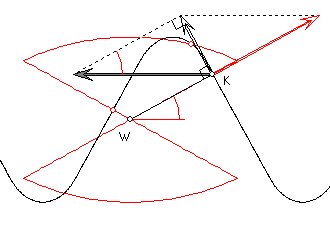
Die Abbildung soll klären, wie die Steigung des s(u)-Graphen zwischen u = 0 und u = 1 durch die
Kontaktkurve festgelegt wird. Man stellt sich einen Stift vor, der die feststehende Kontaktkurve wie bei
einer '8' durchläuft und dabei auf einer nach rechts bewegten Zeichenfläche eine Spur zeichnet. Damit
diese Spur die Verzahnungskurve ist, muss das Verzahnungsgesetz erfüllt sei. Das heißt, dass die
Tangente im Stiftpunkt K orthogonal zur Geraden WK ist. Dies ist äquivalent damit, dass die Summe
der Geschwindigkeitsvektoren des Stiftes relativ zur Kontaktkurve und relativ zur Zeichenfläche
orthogonal zu WK ist. Diese Geschwindigkeitsvektoren und sind rot bzw. grau-schwarz
eingezeichnet. und spannen ein rechtwinkliges Dreieck auf, in dem der rot markierte Winkel
so groß ist wie der Steigungswinkel der Strecke WA der Kontaktkurve. Dieser Winkel wird 'Eingriffs=
winkel' genannt. Der Betrag von ergibt sich, indem man den von durch teilt. Im s(u)-Graph
gilt darum . Daraus ergeben sich die Steigungen in den Intervallen [0 ; 1], [2 ; 4] und [5 ; 6].
Die Steigungen in den Intervallen [1 ; 2] und [4 ; 5] sind wie bei der Zykloidenverzahnung gleich ,
wobei d bzw. r der Abstand des Mittelpunkts vom Bogen von W bzw. A ist.

Die Animation zeigt Verzahnungskurven mit Evolventenverzahnung, bei denen die Kontaktkurve ein
Streckenzug ist. (Die Selbstüberschneidungen der Kurven gibt es auch bei anderen Kontaktkurven.)