Es lebe die Geometrie!

Zu jedem farbigen Pfeil q im Bild des Generators gehört eine Drehstreckung
oder eine Streckspiegelung a, je nachdem, ob ein Plus-Zeichen oder ein
Minus-Zeichen am Pfeil steht. Und zwar ist es die Drehstreckung oder die
Streckspiegelung a, die den schwarzen Pfeil p, Startpfeil genannt, in den
farbigen Pfeil q abbildet. a ist durch p und den farbigen Pfeil q eindeutig
festgelegt. In dem Sonderfall, dass kein Plus- oder Minus-Zeichen am farbigen
Pfeil steht, ist die zugeordnete Abbildung a die konstante Abbildung, die jeden
Pfeil auf den Pfeil q abbildet. Wenn der Generator n farbige Pfeile
enthält, sind dadurch n Abbildungen definiert. Die Figur der Stufe k
setzt sich aus Pfeilen zusammen, die zum Teil nur als Strecken ohne Pfeilspitzen
gezeichnet werden und die auch zusammenfallen können. Jeder dieser Pfeile ergibt
sich dadurch, dass man k von den Abbildungen hintereinanderschaltet
und mit der dadurch entstehenden Abbildung den Startpfeil p abbildet. Die
hintereinander geschalteten Abbildungen müssen dabei nicht verschieden sein.

Rechnerisch kann man die Drehstreckungen und Streckspiegelungen folgendermaßen
verarbeiten: Man führt ein Koordinatensystem ein, in dem der Startpfeil p vom Punkt
(0 ½ 0) zum Punkt (1 ½ 0) zeigt. Ein farbiger Pfeil zeigt dann von einem Punkt (a ½ b)
zu einem Punkt (a + c ½ b + d). Die Drehstreckung oder Streckspiegelung a wird
dann durch die Matrix 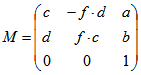beschrieben mit f = 1 für die
Drehstreckung und f = -1 für die Streckspiegelung (projektive Darstellung). Im Fall
ergibt sich für f = 1 eine Drehung oder Verschiebung und für f = -1 eine
Achsen- oder eine Gleit-Spiegelung. Wenn einem Punkt (x ½ y) der Vektor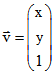

zugeordnet wird, ist das Bild bei der Abbildung durch den Vektor gegeben.

Die Figuren lassen sich auch ohne Verwendung von Abbildungen mit Hilfe von
rekursiven Prozeduren nach dem Turtle-Konzept zeichnen.

Wenn alle Pfeile eine Länge kleiner als 1 haben, konvergiert die Folge der
Figuren der n-ten Stufe für n gegen Unendlich gegen eine Punktmenge M, die
als 'Fraktal' bezeichnet wird. Diese Punktmenge hat die besondere Eigenschaft,
dass jede der Abbildungen M in sich abbildet. Einen Eindruck dieses Fraktals
sollen die Figuren mit der Unterschrift 'Stufe gegen Unendlich' vermitteln.
Diese Figuren entstanden folgendermaßen:

Der Punkt (0 ½ 0) wurde mit einer Abbildung a abgebildet, die zufällig unter
den n Abbildungen ausgewählt wurde. Der Bildpunkt wurde
wiederum durch eine erneut zufällig gewählte Abbildung unter den
abgebildet, u.s.w.. Dieses Verfahren wurde einige zehntausend mal wiederholt.
Die Bildpunkte wurden jedoch erst ab dem 30. Bildpunkt gezeichnet.

Statt des Startpunkts (0 ½ 0) hätte man auch einen anderen Punkt wählen können,
ohne ein wesentlich anderes Ergebnis zu bekommen. Bei der zufälligen Auswahl
der Abbildungen wurden Auswahlwahrscheinlichkeiten proportional zum Quadrat
der Pfeillänge benutzt.