Es lebe die Geometrie!

Höhen im 6-Rechteck mit elliptischen,
euklidischen und hyperbolischen Raumgeraden

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum I'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum II'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_II.pdf

Die Sätze der ebenen euklidischen Dreiecks-Geometrie lassen sich in die Geometrie der Raumgeraden
übertragen, und zwar sowohl bei einer euklidischen Maßbestimmung, als auch bei einer hyperbolischen
oder elliptischen. Siehe dazu auch die Seiten ' euklidische Raumgeraden > Höhen im 6-Rechteck' und
'hyperbolische Raumgeraden > Höhen im 6-Rechteck' .

Der Maß-Bestimmung liegt dabei wie auf den beiden vorangehenden Seiten die symmetrische
Bilinearform für Ebenen-Quadrupel d und e zugrunde. Die
zugehörigen Ebenen D und E sind genau dann orthogonal, wenn f(d ; e) gleich Null ist. Für k = 0 ist die
Maß-Bestimmung euklidisch, für k größer bzw. kleiner Null ist sie elliptisch bzw. hyperbolisch. Geraden
g und h zu Tripel-Paaren (s ; t) und (u ; v) sind orthogonal genau dann wenn die Werte der Bilinearformen
und beide gleich Null sind. Dabei ist
z.B. . Die Gerade g' mit dem Tripel-Paar heißt 'polar' zu g.

Bei der Übertragung der Sätze der ebenen euklidischen Dreiecks-Geometrie wird jeder Eckpunkt des
Dreiecks in eine Achse übersetzt, die zu den beiden Raumgeraden gehört, die den anliegenden Seiten-
Geraden des Eckpunkts entsprechen. Unter einer 'Achse' zweier Geraden g und h verstehen wir dabei
eine Gerade, die orthogonal zu g und h ist und für deren Tripel-Paar (s;t) der Formwert fg((s;t);(s;t))
ungleich Null ist. Im euklidischen Fall k = 0 soll die Achse die einzige Gerade mit diesen Eigenschaften sein.
Dies bedeutet, dass es zu parallelen Geraden g und h keine Achse gibt, da g und h dann unendlich viele
gemeinsame Orthogonalen mit dem Formwert ungleich Null haben. Im Fall k ungleich Null soll die zur Achse
polare Gerade die einzige weitere Gerade mit diesen Eigenschaften sein. Dies bedeutet für den elliptischen
Fall k > 0, dass analog dem Fall k = 0 Clifford-parallele Geraden g und h keine Achse haben. Im Fall k < 0
haben g und h nur dann keine Achse, wenn eine gemeinsame Orthogonale die Kugelfläche
berührt und darum der Form-Wert gleich Null ist.

Der Abstand zwischen zwei Punkten im Dreieck entspricht einem Paar reeller Zahlen mit folgender Bedeutung:
a sei eine gemeinsame Orthgonale der Geraden g und h, die den beide Punkten zugeordnet sind. Dann ist
die erste Zahl die Maßzahl des Winkels zwischen g und h, gemessen als Drehwinkel einer Schraubung längs a,
die g in h oder h in g abbildet. Die zweite Zahl gibt den Abstand der Lotfußpunkte von a auf g und h an. Der
Größe des Winkels zwischen zwei Seiten-Geraden im Dreieck entspricht ebenfalls ein derartiges Zahlen-Paar.

Die Übertragung des Dreiecks ergibt ein räumliches 6-Eck ABCDEF mit drei den Seiten-Geraden
zugeordneten Raumgeraden BC, DE und FA und den Achsen CD, EF und AB dazwischen, die den
Eckpunkten des Dreiecks zugeordnet sind. In der folgenden Animation stimmt die Farbe der Raumgeraden
mit der des jeweils zuerst genannten Punktes überein. Die beiden Zuordnungen 'punkt-analog' und
'geraden-analog' hätten genauso gut vertauscht werden können.

Dass diese Übertragung möglich ist, liegt daran, dass die Relationen zwischen Spiegelungen an Punkten und
an Geraden beim Dreieck weitgehend den Relationen zwischen Spiegelungen an Raumgeraden gleichen.
Darum lassen sich spiegelungs-geometrische Beweise für Sätze der Dreiecks-Geometrie für Raumgeraden
umschreiben.

Die Animation zeigt ein 6-Rechteck ABCDEF und ein zugordnetes euklidisches Analogie-Dreieck unten
rechts. In ABCDEF sind die Achsen gegenüberliegender Kanten-Geraden AB und DE , sowie CD und
FA, und auch DE und BC eingezeichnet, die im Analogie-Dreieck den Höhen entsprechen. Die drei Höhen-
Geraden des 6-Rechtecks ABCDEF haben die violett gezeichnete gemeinsame Achse, die zu dem Schnittpunkt
der Höhen im Analogie-Dreieck gehört. Dem Dreieck der Höhen-Fußpunkte entspricht das mit weißem
Mittelstreifen eingezeichnete 6-Rechteck. Da die Winkel im Höhenfußpunkt-Dreieck von den Höhen halbiert
werden, treffen an jedem grau-schwarz gezeichneten Mitten-Kreuz drei Geraden im gleichen Farbton
aufeinander, die paarweise orthogonal sind. Das Kreuz markiert einen Mittelpunkt auf einer Kanten-Geraden
des 6-Rechtecks mit weißem Mittelstreifen. In Fall von k ungleich Null gibt es noch einen zweiten Mittelpunkt
mit gleichen Eigenschaften, der aber nicht eingezeichnet ist.

Im ersten Teil der Animation wird das elliptische 6-Rechteck zu k = 1 um 360° gedreht. In der oben rechts
angezeigten Gleichung ist die anomal-komplexe Zahl j, die am Schluss der vorhergehenden
Seite ' Clifford-Parallelismus' erklärt wird. Im zweiten Teil wird k bis k = 0 verkleinert. (Die Sprünge, die sich
dabei zeigen, erklären sich daraus, dass von zwei zueinander polaren Achsen nur eine ausgewählt ist.) Das
euklidische 6-Rechteck zu k = 0 wird um 360° gedreht. ist dann die Dualzahl mit dem Quadrat Null, die
am Ende der Seite ' euklidische Raumgeraden > Höhen im 6-Rechteck' erläutert wird. Im dritten Teil sinkt k
weiter bis -1. ist dann die imaginäre Einheit der komplexen Zahlen. Das hyperbolische 6-Rechteck wird
gedreht und anschließend k wieder erhöht.

Die Konstruktion des zum Höhenfußpunkt-Dreieck analogen 6-Rechtecks ist für verschiedene Werte von
k weitgehend gleich. Sie beruht auf der Bestimmung der Achse (also einer gemeinsamen Orthogonalen)
zweier Raumgeraden in normierter Form. Sowohl für euklidische, als auch für hyperbolische oder elliptische
Raumgeraden kann dafür das Kreuz-Produkt für Tripel
und dualer, komplexer bzw. anomal-komplexer Zahlen benutzt
werden, die sich aus den Tripel-Paaren reeller Zahlen (Plücker-Koordinaten)
und ergeben, die wir auch in der Form bzw. schreiben.
Es ist



Da hierbei das innere Produkt im Allgemeinen nicht gleich Null ist, wie für
Plücker-Koordinaten von Geraden verlangt wird, muss m normiert werden. Wie auf der Seiten ' euklidische Raumgeraden>Höhen im 6-Rechteck' und ' hyperbolische Raumgeraden>Orthogonalität' dargestellt wird, kann
man zur Normierung den Term benutzen. Dabei verwenden wir das
Zeichen auch für das innere Produkt ,
das sich unter Verwendung der Verknüpfung dualer, komplexer bzw. anomal-komplexer Zahlen auch durch berechnen lässt. Dies
Verfahren ist nur dann möglich, wenn einen positiven Norm-Wert hat. Wir definieren dabei die Norm
von durch . Wenn diese Norm ungleich Null ist, hat ein multiplikatives Inverses,
denn . Bei dieser Normierung wird nicht nur das innere Produkt
Null für die beiden Tripel von erreicht, sondern sogar, dass gilt. Diese Form einer Normierung
ist im Folgenden stets vorausgesetzt. Wenn sie möglich ist, nennen wir m 'normierbar'.

Für hat 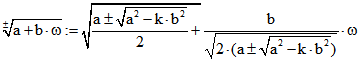mit beiden Vorzeichen das Quadrat
, falls die Norm hiervon positiv ist und . Für k = 0 und a > 0 hat
das Quadrat .

Wenn s und u Tripel dualer, komplexer bzw. anomal-komplexer Zahlen von verschiedenen Geraden g und h
sind, dann ist in den Fällen k = 0 und k > 0 nur dann nicht normierbar, wenn g und h parallel bzw.
Clifford-parallel sind, da dann die Norm von gleich Null ist. Im Fall k < 0 ist m genau dann nicht
normierbar, wenn g und h hyperbolisch orthogonal zu einer Geraden sind, welche die Kugel
berührt. Im Fall der Normierbarkeit gibt es für k = 0 genau eine gemeinsame Orthogonale von g und h mit
einem Tripel m, für das die Norm von ungleich Null ist. Für k ungleich Null gibt es zwei zueinander
polare Geraden, die gemeinsame Orthogonalen von g und h sind, also ein eindeutig bestimmtes Achsen-Paar.

Für elliptische Raumgerade eröffnet die LR-Zerlegung, die auf der vorhergehenden Seite ' Clifford-Parallelismus'
beschrieben wird, ein Verfahren zur Berechnung einer gemeinsamen Orthogonalen zu g und h. Es kann auch
dann auch dann benutzt werden kann, wenn g zu s und h zu u Clifford-parallel sind und darum die Norm von
gleich Null ist. In dem Fall ist die Orthogonale keine Achse, weil es dann unendlich viele
Orthogonalen gibt. Die LR-Zerlegung zum normierten Geraden-Tripel besteht aus dem 'linken'
bzw. 'rechten' Vektor bzw. mit . Zur
Berechnung der Geraden, die elliptisch orthogonal zu g und h ist, bestimmt man ihren linken Vektor als
Einheits-Vektor, der euklidisch orthogonal zu den linken Vektoren von g und h ist. Analog verfährt man mit
den rechten Vektoren. Wenn man auf das Paar dieser beiden Vektoren die auf der vorherigen Seite definierte
inverse Abbildung ILR anwendet, ergibt sich ein Tripel-Paar, das im Allgemeinen noch normiert werden muss.
Falls g und h Clifford-parallel sind, stimmen die linken oder die rechten Vektoren von g und h überein. Dann
hat man mehrere Möglichkeiten für die Wahl eines orthogonalen Vektors. Das Normierungs-Problem tritt dann
nicht auf.

In den letzten 17 Bildern der Gleitschau sind nach den Standbildern der Animation zu dem 6-Rechteck, das
dem Höhenfußpunkt-Dreieck entspricht, Doppelpfeile mit einem Zahlenpaar eingezeichnet. Jedes Zahlenpaar
beschreibt zu Geraden g und h, auf welche die Pfeilspitzen treffen, den zugehörigen Drehwinkel und die
Verschiebungs-Größe . Die Verschiebungs-Größe wird nur für k > 0 im Grad-Maß angegeben. Eine
Schraubung zu längs einer Achse a zu g und h bildet g in h oder h in g ab. ist die elliptische Größe
des Winkel zwischen der ga-Ebene und der ha-Ebene. ist der elliptische Abstand der Punkte an den Spitzen
des Doppelpfeils. Bei der zu a polaren Achse treten die gleichen Zahlen auf, allerdings ist dann die Größe
eines Winkels und eine Verschiebungs-Größe.

Zur Berechnung des Maßes zwischen Ebenen D und E für eine beliebige Maß-Konstante k:

Sei und .
Dann berechnen wir so die Größe fmas(d ; e ; k) zum Geraden-Paar (D ; E):

Der erste Fall liegt für k größergleich Null stets vor, für k kleiner als Null nur dann, wenn die Schnittgerade
von D und E die Kugelfläche trifft. In diesem Fall sehen wir fmas(d;e;k) als Größe des
von D und E bestimmten Winkels an, andernfalls bezeichnen wir den Wert als 'Abstand'. Der dritte Fall tritt
nur ein, wenn k kleiner als Null ist und eine der beiden Ebenen das Innere trifft, die andere aber nicht.

Zur Berechnung des Abstands zwischen Punkten A und B für eine Maß-Konstante k ungleich Null:

Zum Maß zwischen Punkten definieren wir .
(Gelegentlich wird stattdessen definiert. Dadurch
ändert sich die folgende Definition von fpmas aber nicht.)
Sei und .
Dann berechnen wir so die Größe fpmas(a ; b ; k)zum Punkte-Paar (A ; B):

Auch hier trifft der erste Fall für k größer als Null stets zu, aber für k kleiner als Null nur dann, wenn die
Verbindungs-Gerade von A und B das Innere der Kugelfläche nicht trifft. Dass hier ein
Abstand in Grad angegeben wird, kann man dadurch begründen, dass der Abstand zwischen Punkten A
und B auf der Geraden g bei k > 0 mit dem Winkel zwischen den Ebenen übereinstimmt, die mit A bzw. B
und der zu g polare Geraden inzidieren. Der dritte Fall tritt nur ein, wenn k kleiner als Null ist und einer der
beiden Punkte im Innern liegt und der andere außerhalb der Kugel.

Für k = 0 wird der Abstand von Punkten A und B mit den Quadupeln und
wie üblich in der euklidischen Geometrie durch definiert.

Zusammenhang zwischen den Maß-Funktionen (fg ; gg) einer Geraden,
dem Drehungs-Winkel und derVerschiebungs-Größe :

Wir erweitern die Kosinus-, die Sinus-Funktion und ihre Umkehrfunktionen für duale, komplexe
bzw. anomal-komplexer Zahlen zu k = 0, k < 0 bzw. k > 0 durch Rückführung auf diese Funktionen
für reelle Zahlen oder im Fall k < 0 auf diese Funktionen für komplexe Zahlen mit k = -1. Dabei ist
sign(k) gleich 1, 0 bzw. -1 für k > 0, k = 0 bzw. k < 0.
(Für k < 0 ist und . )
Für k ungleich Null ergibt sich durch Anwendung einer LR-Zerlegung :




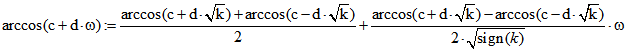
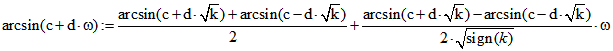
Dann ist , aber nur mit eingeschränktem
Definitions-Bereich. Für k > 0 ist .

Für k gleich Null gilt mit bei Verwendung der Formel :





Um die Maß-Zahlen und zum Geraden-Paar (g;h) zu bestimmen, kann man noch einen anderen
Weg gehen, als den über Maße von Punkten und Ebenen, die mit einer gemeinsamen Orthogonalen
von g und h inzidieren. Welche der beiden Zahlen in Bezug auf eine bestimmte Achse den Drehungs-
Winkel angibt und welche den Verschiebungs-Winkel, bleibt dabei allerdings bei k > 0 unklar. Der Weg
führt über die Werte von fg und gg. Wenn die Tripelpaare (s;t) und (u;v) von g und h normiert sind, gilt nämlich
. Die Anwendung von arccos auf beiden
Seiten ergibt oder , die zweite Möglichkeit aber nur bei k > 0.
Man kann für beliebiges k ungleich Null mit den Bezeichnungen
und
auch
in folgender Weise darstellen:


.

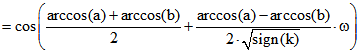
Zusammenhang zwischen den Maß-Funktionen (fg ; gg) einer Geraden
und der Maß-Funktion f bzw. fp für Ebenen bzw. Punkte:

a, b, c, d seien Quadrupel von Ebenen A, B, C, D und g bzw. h die Schnitt-Gerade von A und B bzw.
C und D zum Tripelpaar (s;t) bzw. (u;v). Dann ist
und .

a, b, c, d seien Quadrupel von Punkten A, B, C, D und g bzw. h die Verbindungs-Gerade von A und B bzw.
C und D zum Tripelpaar (s;t) bzw. (u;v). Dann ist
und .

Zu gemeinsamen Beweisen geometrischer Sätze über 6-Rechtecke
euklidischer, hyperbolischer und elliptischer Raumgeraden

Euklidische, hyperbolische und elliptische Raumgeraden haben gemeinsam, dass man sie durch Tripel
hyperkomplexer Zahlen (duale, komplexe bzw. anomal-komplexe Zahlen) darstellen
kann und dabei metrischen Eigenschaften wie die Orthogonalität durch die symmetrische Bilinearform bestimmt werden. Zwei hyperkomplexe Zahlen
und ergeben das Produkt , wobei die
reelle Zahl für euklidische Raumgeraden Null ist, für hyperbolische negativ ist und für elliptische
positiv. Für die Menge dieser hyperkomplexen Zahlen mit dieser Multiplikation und der Addition
gilt das Assoziativ-Gesetz, das Distributiv-Gesetz und das Kommutativ-
Gesetz, aber nur für k < 0 gibt es zu jede Element in dieser Menge ein y mit
. Für k = 0 gibt es ein derartiges multiplikatives Inverses nicht, wenn ist.
ist dann Nullteiler, weil es ein Element (z.B. ) ungleich 0 gibt, dessen Produkt mit x
gleich 0 ist. Für k > 0 fehlt ein Inverses in den Fällen und . Auch diese
Ausnahmen sind Nullteiler, denn .

Im Folgenden soll an dem Beispiel des 6-Rechtecks, das dem Höhenfußpunkt-Dreieck der zweidimensionalen
Geometrie entspricht, gezeigt werden, wie man spiegelungsgeometrische Schlussweisen auf Raumgeraden
übertragen kann, die für ebene Dreiecke in folgendem Lehrbuch dargestellt wird:
(*) ' F.Bachmann, Aufbau der Geometrie aus dem Spiegelungsbegriff, Springer 1973'

In Satz 43 der im Kopf dieser Seite angegebenen Pdf-Datei wird gezeigt, dass sich die Spiegelung einer
Raumgeraden g zum Tripel s an einer Raumgeraden h zum normierbaren Tripel u durch durch den Term
beschreiben lässt, der auch in der ebenen Geometrie verwandt wird. Für hat die zu
h polare Gerade h' den gleichen Term, da zu h' das Tripel gehört. Der Term ist nur dann definiert, wenn
es zu ein multiplikatives Inverses gibt. Dies Inverse fehlt nur dann, wenn k < 0 ist und g die Kugel mit
dem Radius berührt. Andernfalls lässt sich u durch Multiplikation mit einer reellen Zahl so normieren,
dass gilt. Im Folgenden gehen wir stets von so normierten Tripeln aus. Die Gerade zu u nennen wir
hier 'Trägergerade von '.

Die Verkettung zweier Spiegelungen ist genau dann eine Spiegelung , wenn ist. Dann gibt
es zu der Determinanten Det({x;y;z}) ein multiplikatives Inverses und . Wenn die Geraden zu
u, v und w eine gemeinsame normierbare Orthogonale haben, dann ist eine Spiegelung zum Tripel
. Siehe dazu I.9 und I.10 in Text 'Plane elliptic geometry over rings' von
Frieder Knüppel und Edzard Salow ( https://projecteuclid.org/euclid.pjm/1102701007).

Die Matrix der Spiegelung zum normierten Tripel u ist ,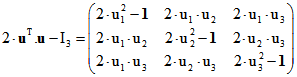
wobei die Spalte ist, die durch Transponieren der Zeile u entsteht und die Matrix
mit drei fetten Einsen in der Hauptdiagonalen und sonst nur Nullen. Man errechnet
und .
Falls die Verkettung dreier Spiegelungen mit der Verkettung zweier Spiegelungen
übereinstimmt, dann ist , also .
Wenn mit Tripeln reeller Zahlen r und s, dann sind r und s im Allgemeinen keine
Vektoren mit , weil noch nicht normiert ist. Die Normierung von
zu einem Tripel einer gemeinsamen Orthogonalen der Geraden zu p und q, zu der höchstens die dazu
polare Gerade eine weitere Orthogonale ist, gelingt nur bei positiver Norm von .

Satz: Gegeben seien drei normierte Geraden-Tripel a, b und c, für welche die Norm von
positiv ist, und zwei normierte Geraden-Tripel p und q, für die
gilt. Dann ist im Fall k ungleich Null normierbares Tripel zu einem
eindeutig bestimmten Achsen-Paar der Trägergeraden zu p und q. Diese sind also
orthogonal zu beiden Geraden des Paars. Im Fall k gleich Null gibt es nur eine Achse
der Trägergeraden zu p und q.

Diesen Satz brauchen wir in der folgenden Argumentation zu einem 6-Rechteck.
Dabei benutzen wir Bezeichnungen aus (*), S.58, auch in der folgenden Zeichnung.

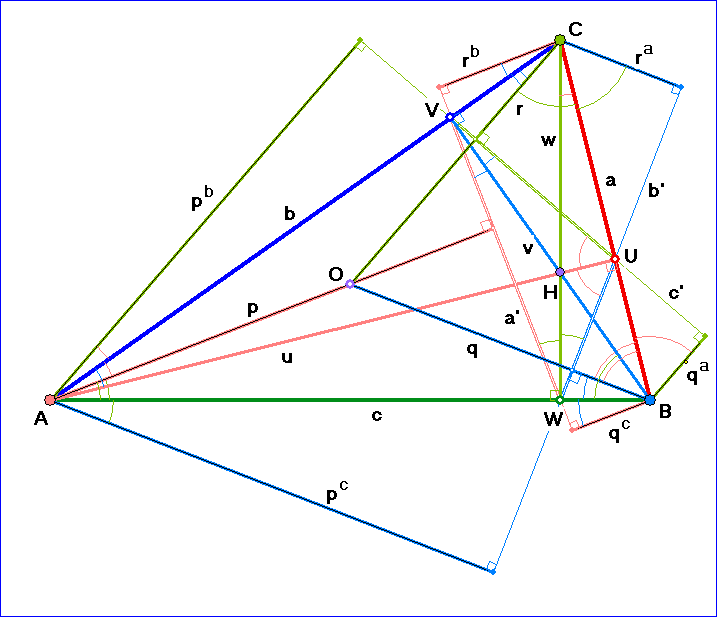
Wir formulieren den Höhensatz in (*), S.56, mit den Bezeichnungen des obigen Analog-Dreiecks in
folgender Weise um. Dabei bezeichnen wir z. B. die Spiegelung mit dem nicht fetten Buchstaben a.
Wir kürzen die Verkettung cpc mit ab. Dies ist die Spiegelung an der Geraden zum Tripel .


Satz : sei die Menge der Spiegelungen an normierbaren Geraden des euklidischen,
hyperbolischen oder elliptischen Raums. Sei .
Für die Tripel a, b und c zu a, b, c sei die Norm von positiv.
Die Verkettungen U := ua, V := vb und W := wc, sowie p := buc, q := cva
und r := awb seien ebenfalls Elemente in . Dann folgt .
Außerdem gibt es im Fall k ungleich Null ein Achsen-Paar g, g', zu dem die
Trägergeraden der Spiegelungen U, , , W, , q, und orthogonal
sind. Für k gleich Null gibt es nur eine Achse mit dieser Eigenschaft.

Beweis: Da jede Spiegelung involutorisch ist, die Verkettung mit sich selbst also die identische
Abbildung ergibt, gilt ua = au , cw = wc, buc = cub und awb = bwa.
Daraus folgt cbu = cbucc = ccubc = ubc und wba = aawba = abwaa = abw.
Man errechnet damit




abc stimmt also mit der Verkettung der Spiegelungen von U und , von und W , von und q
und auch von und überein. Darum gibt es nach dem vorhergehenden Satz im Fall k
ungleich Null ein gemeinsames normiertes Achsen-Paar g, g' orthogonal zu den Trägergeraden,
zu denen U, , , W, ,q, und Spiegelungen sind. Im Fall k gleich Null gibt es nur
eine derartige Achse. Die zugehörige Spiegelung bezeichnen wir mit b'. Wenn man eine Trägergerade
von b' mit a spiegelt, ergibt sich eine Achse zu den Trägergeraden von V, und U, dessen zugehörige
Spiegelung wir mit c' bezeichnen. Da die Trägergeraden von U, q und W eine gemeinsame Achse
haben, folgt .