Es lebe die Geometrie!

Die Kette alternierender 2m-Zykloiden

Unter einer alternierenden 2m-Zykloide verstehen wir eine Kurve, die sich aus abwechselnden
Bögen von 2m-Zykloiden und -2m-Zykloiden so zusammensetzen, dass die Verknüpfungspunkte ein
regelmäßiges 2m-Eck bilden. Eine alternierende 4-Zykloide besteht also aus zwei Astroiden-Bögen
und zwei 4-Zykloiden-Bögen, die innen bzw. außen an die Seiten eines Quadrats angesetzt sind.

Die Animation zeigt die Verkettung von alternierenden 2m-Zykloiden für ganzzahlige Werte von m
ungleich Null zwischen -5 und 5. Alle Zykloiden berühren sich in einem Punkt der roten Kontakt-
Kurve, die sich aus zwei Kreisen vom Radius 1 zusammensetzt, die sich im Koordinatenursprung
berühren. Jede 2m-Zykloide dreht sich um den Punkt (0 ; 2m), und zwar so, dass der gemeinsame
Kontaktpunkt K die Kontaktkurve in Form einer '8' durchläuft. Die gemeinsame Tangente ist dabei
stets orthogonal zur Verbindungsgeraden vom Kontaktpunkt mit dem Ursprung. Wenn man die
Kurven als Ränder von Zahnrädern betrachtet, ist diese Orthogonalität eine Folge des Verzahnungs-
Gesetzes der Getriebelehre. Der Koordinaten-Ursprung hat dann die Rolle des 'Wälzpunkte'.

Um diese alternierenden 2m-Zykloiden in komplexer Darstellung anzugeben, verwenden wir die
Abkürzung . Dabei ist n eine ganze Zahl und eine reelle Zahl zur Festlegung
der Lage des Kontaktpunktes K. Dann ist die 2m-Zykloide gegeben durch den Graphen der Funktion

.

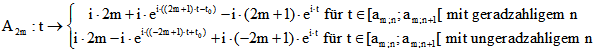Der Kontaktpunkt K ergibt sich für t = 0. Für erhält man die Punkte, in denen die konvexen
und konkaven 2m-Zykloiden-Bögen stetig differenzierbar aneinander anschließen. Für
bei ganzzahligem j mit mit geradzahligem n gilt ; in dem zugehörigen
Punkt berühren sich die alternierende 2m-Zykloide und die alternierende 2(m+1)-Zykloide. Sie liegen auf
dem Kreis mit dem Radius 2m+1, der in der Animation grau eingezeichnet ist. Auf diesem Berührpunktkreis
gibt es m oder m+1 Berührpunkte, je nachdem der rote Berührpunkt auf den oberen oder dem unteren
Kreis der roten Kontaktkurve liegt. Während sich im diesem rot berandeten Berührpunkt stets gleichsinnig
gekrümmte Teile der beiden alternierenden Zykloiden treffen, berührt in den schwarz berandeten Punkten
auf dem Berührpunktkreis stets ein konkaver Bogen einen konvexen Bogen. Wenn zwei benachbarte dieser
schwarzen Berührpunkte einen Bogen auf dem Berührpunktkreis begrenzen, der den Punkt W(0 ; 0) in der
Mitte der roten Kontaktkurve nicht enthält, dann hat der Bogen die Länge .

Die schwarze Kurve gehört zu der Funktion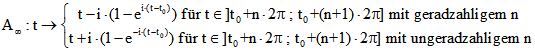
Wir nennen sie alternierende -Zykloide. Die Bögen sind die Spuren eines Punktes auf dem Rand eines
Gangkreises vom Radius 1, der auf der Rechtsachse abrollt, wobei sich der Gangkreis alternierend auf
verschiedenen Seiten der Achse befindet.

Hier wurden zu den alternierenden 2m-Zykloiden neben den Berührkreisen die zugehörigen Rastkreise
vom Radius 2m hinzugezeichnet. Sie trennen die 2m-Zykloiden-Bögen von den -2m-Zykloiden-Bögen.
Wenn man die alternierenden 2m-Zykloiden als Zahnräder deutet, haben diese Kreise die Rolle von
Wälzkreisen. Das heißt, dass sich die Zahnräder so drehen, als würden die zugehörigen Wälzkreise in
ihrem gemeinsamen Berührpunkt, dem Wälzpunkt W=(0 ; 0), ohne zu Rutschen aneinander abrollen.
Diese Zahnräder sind aber zur Kraft-Übertragung wenig geeignet, da es zwischen dem Eingriff eines
Zahns des antreibenden Rads und dem Eingriff des nächsten eine Lücke gibt. (Dieser Mangel wäre
vielleicht durch eine Schrägverzahnung auszugleichen.)

Bei einer Deutung als Zahnräder stellt die schwarze Kurve in der Animation ganz oben eine Zahnstange dar,
die sich so bewegt, als würde ihre Achse von den Wälzkreisen ebenfalls ohne zu Rutschen angetrieben.

Die Form der 2m-Zykloiden kann man sich in folgender Weise zustande gekommen denken: Man
stellt sich die rote Kontaktkurve als feste Schiene vor, auf der eine Stift in Form einer '8' geführt wird.
Wenn man den Stift auf der Schiene bewegt, wird dabei ein Rad unter dem roten Kreis mitbewegt,
als wäre der Stift mit seinem Rand verbunden. Dieses Rad treibt einen Wälzkreis mit einer daran
befestigten Zeichenfläche an. Dann zeichnet der Stift auf der Zeichenfläche eine alternierende
2m-Zykloide. Zum Zeichnen der schwarzen alternierenden -Zykloide muss entsprechend
statt des Wälzkreises eine Stange angetrieben werden, an der die Zeichenfläche befestigt ist.

Die Animation zeigt eine bemerkenswerte geometrische Eigenschaft der Berührpunkte der
alternierenden 2m-Zykloide mit der alternierenden 2(m+1)-Zykloide:

In jedem Berührpunkt P der beiden alternierenden Zykloiden, der nicht auf der roten Kontaktkurve
liegt, ist die Tangente orthogonal zur Verbindungsgeraden von P mit dem Wälzpunkt W (0 ; 0). Die
Punkte W, P und T (0 ; 4m+2) bilden darum ein rechtwinkliges Dreieck im grauen Berührpunktkreis.

Die Animation und die in der Gleitschau folgenden Bilder zeigen auch den Zusammenhang zwischen dem
Steigungswinkel der Verbindungsgeraden von W mit dem Berührpunkt K auf der roten Kontaktkurve und
dem Steigungswinkel der Geraden WP für einen Berührpunkt P auf dem grauen Berührpunktkreis. Die
Steigungswinkel für die anderen schwarz berandeten Berührpunkte ergeben sich durch Addition eines
ganzzahligen Vielfachen von .