Es lebe die Geometrie!

Steiner-Zykloide und Steiner-Gleichdick

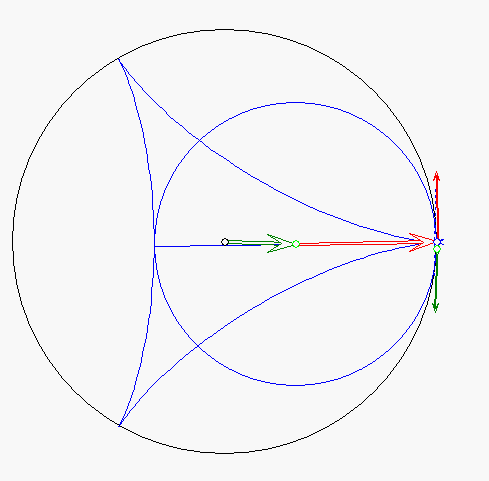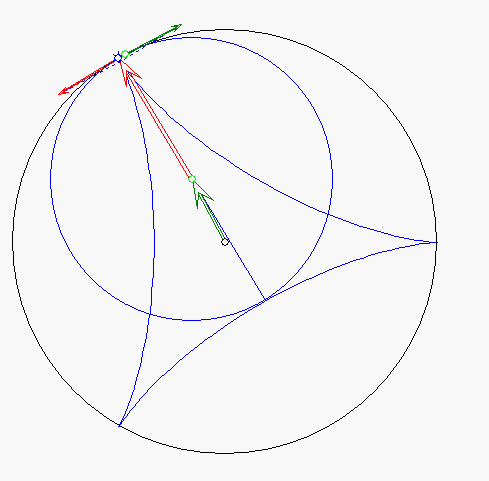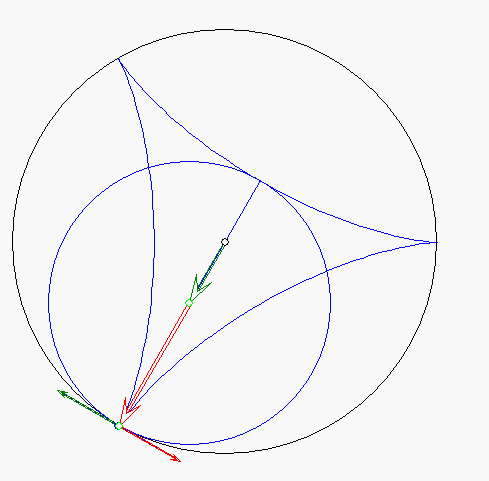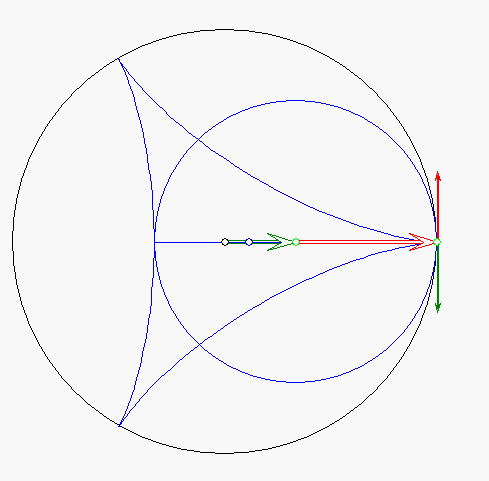
Steiner-Zykloide mit Geschwindigkeitsvektoren
Der kleine Kreis, der Gangkreis, rollt an dem großen Kreis, dem Rastkreis, mit konstanter Geschwindigkeit
ohne zu Rutschen ab. Die Endpunkte bewegen sich dabei auf der Steiner-Zykloide und der rot gezeichnete
Durchmesser verläuft tangential dazu. Die Geschwindigkeit des Mittelpunktes des Gangkreises wird durch den
grünen Pfeil angegeben, die Geschwindigkeit der Eigendrehung durch den roten Pfeil. Die Geschwindigkeiten
stimmen stets im Betrag überein. Der rote Pfeil ist immer senkrecht zum Durchmesser gerichtet, der grüne Pfeil
aber senkrecht zur Verbindungsgeraden der Mittelpunkte der beiden Kreise. Der blaue Pfeil zeigt die resultierende
Geschwindigkeit eines Durchmesser-Endpunktes; sie ist ebenfalls tangential zur Steiner-Zykloide gerichtet.
Wenn der Richtungswinkel des resultierenden Geschwindigkeitsvektors ist, der des roten Durchmesserpfeils
und der des roten Pfeils zur Gangkreismitte , dann gilt und .

Steiner-Zykloide mit Evolvente
Die hellblaue Kurve ist die Evolvente der dunkelblauen Steiner-Zykloide durch deren Bogen-Mitten. Sie
ist selbst eine Steiner-Zykloide. Wenn man einen Stab mit einem markierten Punkt P so tangential an die
dunkelblaue Kurve anlegt, dass P in einer Spitze der hellblauen Kurve liegt, und den Stab dann an der
dunkelblauen Kurve abrollt, bewegt sich P auf der hellblauen Kurve. Dies zeigt sich an dem Durchmesser-
Endpunkt der hellblauen Kreises, der an dem kleinen schwarzen Rastkreis abrollt. Die entsprechenden
Längen der großen und der kleinen Zykloide verhalten sich wie 3 : 1. Wenn a bzw. b der Richtungswinkel
des großen schwarzen bzw. roten Pfeils ist, dann ist der Richtungswinkel des entsprechenden kleinen Pfeils
180° - 2a bzw. 180° + a . Sowohl die dunkelblaue Durchmessergerade als auch die hellgrüne senkrecht
dazu durch die Spitze des kleinen roten Pfeiles sind Tangenten der großen Steiner-Zykloide. Ebenso die
gelbe Gerade durch die Berührpunke dieser beidenTangenten.

Steiner-Zykloide mit Steiner-Gleichdick
Die Länge des langen roten Pfeils verhält sich zu der des kurzen wie 8 : 3. Die beiden Pfeile sind
gleichgerichtet. Die Mitte des langen roten Pfeils bewegt sich auf der hellblauen Evolventenkurve der
dunkelblauen Steiner-Zykloide. Der lange rote Pfeil rollt an der Zykloide ab. Seine Endpunkte bewegen
sich dabei auf der roten Kurve. Diese schließt ein Gleichdick ein, d. h. eine Fläche, die in jeder Richtung
die gleich Breite hat, nämlich 8/9 der Breite des großen Rastkreises.

Steiner-Gleichdick mit umschließendem Quadrat
Die umschließenden Quadrate des Steiner-Gleichdicks berühren das Gleichdick in vier Punkten. Die
Verbindungsgeraden von zwei dieser Punkte auf gegenüberliegenden Seiten stehen snkrecht aufeinander
und verlaufen tangential zur Steiner-Zykloide. Ihr Schnittpunkt liegt auf dem Rastkreis der Evolvente
durch die Bogen.Mitten. Die pinkfarbene Mitte des Quadrats liegt auf dem Rastkreis der Evolvente.