Es lebe die Geometrie!

Fünfeck im rechtwinkligen Dreieck

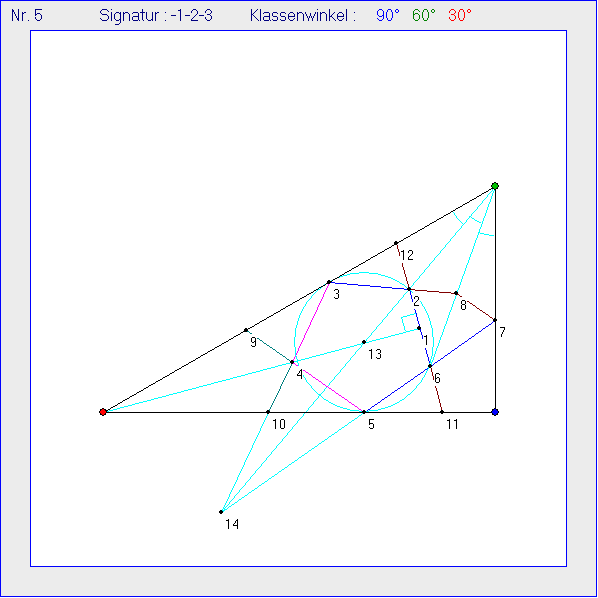
Die Gleitschau zeigt die Konstruktion eines Bandwerks aus einem besonderen 'Drittelungs-Fünfeck' in einem
rechtwinkligen Dreieck. In den ersten 14 Bildern der Gleitschau hat das Dreieck ABC die Innenwinkel-Größen
30°, 90° und 60° und in den folgenden sieben Bildern (Nr. 15 bis 21) die Größen 45°, 90° und 45°. In diesen
Fällen werden nur Achsen-Spiegerlungen als Nachbar-Bewegungen benutzt. In den letzten sieben Bildern
(Nr. 22 bis 28) zur Signatur -1-23 wird bei der Seite 3 des Dreiecks ABC eine Punktspiegelung am
Mittelpunkt verwandt.

Wir beziehen uns zunächst auf das Dreieck ABC der ersten 21 Bilder. Die Rechnungen gelten aber auch
für das Dreieck ABC zur Signatur -1-23. Vier Punkte des Drittelungs-Funfecks liegen auf dem Inkreis des
Dreiecks, das gebildet wird von zwei Seiten und einer Drittelungsgeraden von ABC . Im ersten Bild der
Gleitschau sind dies die Seiten AB, AC und die Verbindungsgerade von C mit dem Punkt P6, der neben
P3 und P5 Berührpunkt dieses Inkreises ist. Ein weiterer Eckpunkt des Fünfecks ist der Schnittpunkt P2
der zweiten Drittelungsgeraden durch C mit dem Inkreis. Der letzte Eckpunkt P4 ist der Schnittpunkt der
Geraden, die sich bei Spiegelung der Geraden P5P6 bzw. P2P3 an den Seitengeraden AB bzw. AC ergeben.
w sei ein Drittel der Größe des Winkels ACB. P4 liegt nur dann auf dem Inkreis, wenn w 18° beträgt, also
ein Fünftel von 90°. Da das Dreieck CP6P13 bei P6 rechtwinklig ist, hat der Winkel P2P13P6 die Größe
90° - w. Wegen der Gleichschenklichkeit des Dreiecks P6P2P13 hat der Winkel P13P2P6 die Größe
. Der Richtungswinkel der gerichteten Geraden P2P6 errechnet sich mit Hilfe des
Richtungswinkels von CP2 zu . Daraus folgt,
dass in jedem rechtwinkligen Dreieck die Winkelhalbierende bei A senkrecht zur Geraden P2P6 steht,
denn deren Richtungswinkel hat die Größe . Folglich ist das Fünfeck P2P3P4P5P6
symmetrisch zur Winkelhalbierenden durch A. Die Strecke P2P3 ist also nicht nur gleich lang wie P2P6,
sondern auch gleich lang wie P5P6. Da die Winkel P6P5P13, P13P5P4 und P13P6P5 gleich groß sind,
haben die Innenwinkel des Fünfecks bei P5, P6, P2 und P3 die Größe 90° + w, folglich der Winkel bei P4
die Größe . Das Drachenviereck P2P6P7P8 hat drei gleich große
Winkel der Größe

In den vier Serien der Gleitschau ist w nacheinander 20° (Nr. 1 bis 7), 10° (Nr. 8 bis 14),
15° (Nr. 15 bis 21) und 18° (Nr. 22 bis 28).

An Hand der Dreiecks AP13C errechnet man für das Verhältnis der Streckenlängen CP3 zu CA: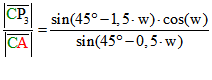
.
Für w = 18° ist dies gleich 0,5. Für das Verhältnis der Streckenlängen CP12 bzw. P9A zu CA ergibt sich: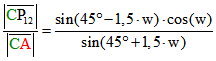

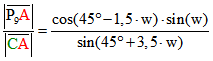
Für w = 18° ist dies beides gleich (ca. 0.309017). Die Menge der Treffpunkte des Billard-Pfads auf der
Seite AC ist dann also punktsymmetrisch zum Mittelpunkt. Da außerdem die Winkelgrößen von CP12P11
und AP9P5, nämlich und für w = 18° übereinstimmen, ist die Signatur -1-23 zur
Erzeugung eines Bandwerks mit Hilfe eines Billard-Pfads in den letzten Bildern der Gleitschau (Nr. 22 bis 28)
verwendbar. Die Drittelungs-Fünfecke sind dann regelmäßig und die Sterne um die grünen Eckpunkte
regelmäßige 10-Sterne.

Die Seitengerade AB bzw. AC sei c bzw. b genannt, und die Gerade CP6 bzw. CP2 bzw. AP4 sei mit d bzw.
e bzw. f bezeichnet. Dann gilt für die Hintereinanderschaltung der Achsenspiegelungen an e, b, f, c, d und f : ist die Spiegelung an dem Punkt P2. Denn diese Bewegung
bildet die Gerade P2P6 und den Punkt P2 in sich ab, ist aber nicht die identische Abbildung. Dies gilt auch
dann, wenn zwar die Winkel ACP2 und P6CB gleich groß sind, nicht aber mit dem Winkel P2CP6 in der
Größe übereinstimmen.

In Bild 1 der Gleitschau sind alle Strecken mit Ausnahme der hellblauen gleichfarbig gezeichnet, deren
Längen übereinstimmen. Für die Konstruktion eines Bandwerks ist insbesondere die Längengleichheit
der grünen und der braunen Strecken wichtig, weil sie in der durch Spiegelungen erzeugten Kachelung
regelmäßige Sterne ergeben. Wir benutzen eine Spiegelungsstrecke auf der Geraden CP6 und den
Billard-Pfad P10P3P8P7P5P9 mit drei Seiten-Reflexionen und einen zweiten Pfad P11P12 ohne Seiten-
Reflexionen. Jede im Bandwerk berandete Fläche ist dann kongruent zu einer der folgenden Polygon-Flächen:

einem regelmäßigen Stern mit den Innenwinkeln und ,

einem regelmäßigen Stern mit den Innenwinkeln und

dem Fünfeck P2P3P4P5P6 mit den Innenwinkeln und ,

dem Drachenviereck P2P6P7P8 mit den Innenwinkeln und ,

dem Drachenviereck, das sich sich durch symmetrische Ergänzung des Dreiecks
P5P4P10 ergibt, mit den Innenwinkeln , und ,

einem Achteck mit zwei senkrechten Symmetrieachse und den Innenwinkeln und .

Die Gleitschau zeigt, wie ein Bandwerk mit 11-Sternen (nach Jay Bonner) aus zwei Billard-Pfaden in
einem Trapez ABCD mit zwei rechten Winkeln mit Hilfe der oben beschriebenen Drittelungs-Fünfecke
entsteht. Die Signatur ist dabei -1-2-34. Die Nachbar-Bewegungen zu den Seiten 1 bis 3 sind also
Achsenspiegelungen und die zur Seite 4 eine Punktspiegelung am Seiten-Mittelpunkt. Das Trapez wird
aus drei "zweidrittel" Exemplaren eines rechtwinkligen Dreiecks mit einem Innenwinkel für
zusammengesetzt. Dabei wird das zweite Dreieck an der Hypotenuse ED des ersten und das dritte an der
längeren Kathete EF des zweiten gespiegelt (siehe dazu Bild 1 der Gleitschau). Das vierte Dreieck EBC
hat als Seitengerade eine Drittelungsgerade durch C im Dreieck, das die Spiegelung von ECF an EC
ergibt. Das Trapez hat also die Innenwinkel 90°, 90°, 5w und 6w. Durch die Spiegelungen der Dreiecke
wird erreicht, dass die zugehörigen Drittelungs-Fünfecke sich um den Punkt E herum in das Trapez
berührend einfügen und in den Berührpunkten jedes der Fünfecke im Nachbarn für die dort zusammen=
treffenden Seiten eine geradlinige Fortsetzung findet.

Für innere Spiegelungen benutzen wir die sechs grauen Strecken auf den Seite ED, EF und EC, die von E
und D bzw. F bzw. C ausgehen, sowie drei Strecken mit den Anfangspunkten D, F und C in Richtung der
zu den Fünfecken gehörigen Drittelungs-Geraden. Die zehnte Spiegelungsstrecke geht von E aus und schließt
mit EB einen Winkel von ein. Diese Strecke liegt auf einer Geraden g mit folgender Eigenschaft:

Die Symmetrieachse h des Drittelungs-Fünfecks zwischen EC und BC geht durch E und schließt mit EC
einen Winkel der Größe ein. Darum gilt für die Hintereinanderschaltung der Spiegelungen an
EC, h und EB: .

Wir benutzen zwei Bilard-Pfade, die auf der Trapez-Seite AB unter den Winkeln und
starten. Die Anfangspunkte P0 und P0' liegen auf Seitengeraden des Drittelungs-Fünfecks im
Dreieck AED . Dabei gilt und . Dann wird jede Seite der Fünfecke
von einem der Billard-Pfade durchlaufen und das Bandwerk bildet regelmäßige 11-Sterne. Allerdings sind die
9-Sterne nicht regelmäßig.

Die Kachelung wird an der Seite 4 zwischen den roten Eckpunkten durch eine Punktspiegelung an der Mitte
der Seite fortgesetzt. Damit dabei auch das Bandwerk fortgesetzt wird, muss die Menge der Treffpunkte
des Billard-Pfads mit Seite 4 symmetrisch zum Mittelpunkt sein. Wenn der Anfangspunkt des ersten Pfades
verrückt wird, kann man dies durch Verschiebung vom Startpunkt des zweiten Pfads erreichen. Das Bandwerk
hat dann aber nur noch unreglmäßige 11-Sterne.

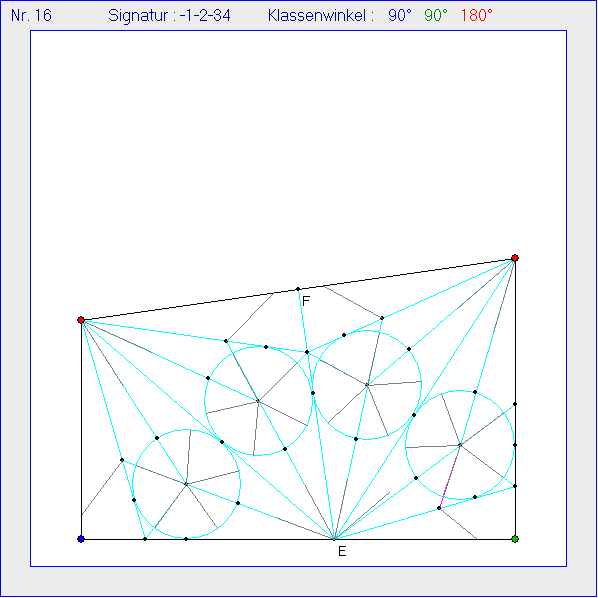
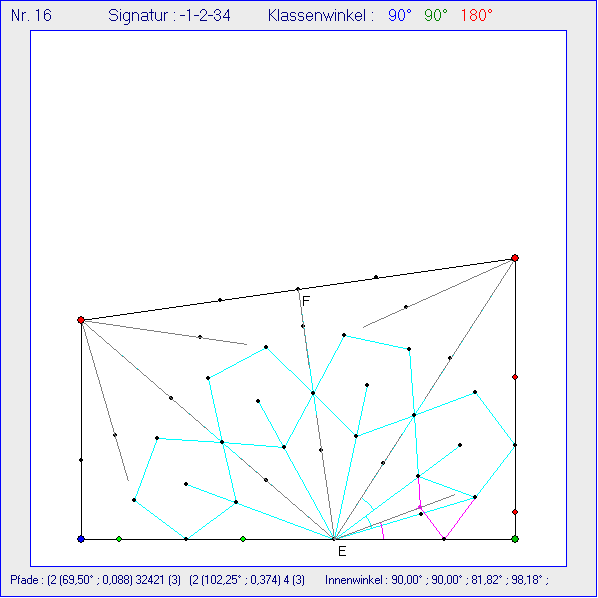
Wie in der vorangehenden Gleitschau wird hier ein Trapez, das Ausgangskachel einer Kachelung zur
Signatur -1-2-34 sein kann, in vier rechtwinklige Teildreiecke aufgeteilt, von denen drei kongruent sind.
Die Dreiecke werden aber anders gefüllt, nämlich mit Streckenzügen wie in der dritten Gleitschau der
vorigen Seite Bandwerk 2. Die Innenwinkel des Trapezes bei C und D wurden in fünf bzw. sechs
Teilwinkel der Größe unterteilt. Benachbarte hellblaue Strecken durch E schließen einen
Winkel der Größe ein. Die äußeren beiden hellblauen Strecken durch E bilden mit AB
links einen gleich großen Winkel, rechts aber nicht. Die Kreise sind Inkreise von durch hellblaue
Strecken gebildeten Teildreiecken. Von den fünf schwarzen Punkten darauf sind drei Berührpunkte
und die beiden anderen halbieren die durch die Berührpunkte begrenzten Kreisbögen. Vier der
fünf Punkte sind Eckpunkte eines Drittelungs-Fünfecks, der fünfte liegt auf der Geraden durch E,
den Inkreis-Mittelpunkt und den fünften Punkt des Drittelungs-Fünfecks.

Zur Konstruktion von Billard-Pfaden benutzen wir als Spiegelungs-Strecken die grau gezeichneten
Verbindungsstrecken der Inkreis-Mittelpunkte mit den fünf Kreisbogen-Mitten, außerdem je zwei Strecken
auf hellblauen Strecken durch C und D und drei derartige Strecken durch E. Ein vierte von E ausgehende
graue Spiegelungs-Strecke schließt mit EC einen Winkel der Größe w ein. Die restlichen vier grauen
Spiegelungs-Strecken ergeben sich folgendermaßen: Man verlängert eine der von einem Inkreis-Mittelpunkt
ausgehende graue Strecke bis zur nächsten hellblauen Seite und spiegelt daran. Drei dieser vier letzten
Spiegelungs-Strecken sind dann parallel zu einer der Spiegelungs-Strecken, die von einem der Mittelpunkte
ausgehen, nicht aber die vierte rechts unten.

Die Bilder Nummer 2 bis 6 zeigen ein Bandwerk, das durch einen periodischen Billard-Pfad mit Startpunkt
F erzeugt wird. In den Bildern 7 bis 9 wird ein weiterer Pfad hinzugefügt, der aber noch nicht zu einem
Bandwerk führt. Dies kommt erst durch einen dritten Pfad in den Bildern 10 bis 13 zustande, dessen
Startpunkt aus dem des zweiten Pfads durch Spiegelung an F entsteht. Der zugefügte vierte Pfad in den
Bildern 14 bis 20 vervollständigt das Bandwerk so, dass sich um die roten Eckpunkte regelmäßige
11-Sterne ergeben. Der 9-Stern um E ist allerdings nicht regelmäßig. In den Bildern 21 bis 41 wird die
entsprechende Abfolge nach Verrückung des Startpunkt vom ersten Pfad nach links wiederholt, wobei
die übrigen vier Pfade so angepasst wurden, dass die 11-Sterne bei den roten Eckpunkten wieder
regelmäßig sind. In den Bildern 42 bis 61 wurde der Startpunkt des ersten Pfads nach rechts verschoben.
Die Startrichtung aller vier Billard-Pfade wurde so gewählt, dass die erste Billard-Strecke durch den
schwarzen Kreispunkt verläuft, der dem Startpunkt am nächsten liegt.

Zur Begründung für die Spiegelungs-Strecke unten rechts (im letzten (62.) Bild die Strecke EP):
Bei der Erzeugung eines Bandwerks mit Hilfe eines Billard-Pfads ist es wünschenswert, dass bei Verrückung
von Anfangspunkten bei festgehaltenen Spiegelungs-Strecken möglichst viele Regelmäßigkeiten erhalten
bleiben. Das wird hier dadurch erreicht, dass die Hintereinanderschaltung der Spiegelungen an den Geraden
EC, EP, EB, QR und EQ mit der Spiegelung an QS übereinstimmt. Denn die Winkel BEQ und PEC sind
wegen gleich groß und darum gilt .

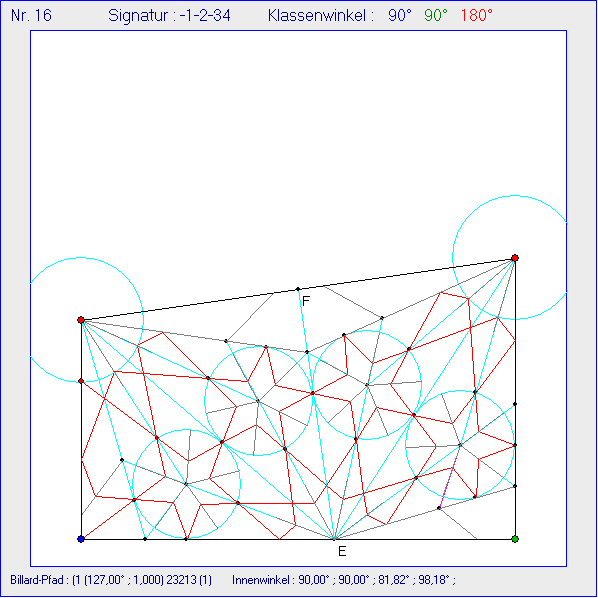
In dieser Gleitschau wurden in das Trapez drei Strecken eingefügt, an denen der Billard-Pfad nicht
gespiegelt, sondern reflektiert wird. Zwei dieser Strecken bilden mit CD ein gleichschenkliges Dreieck
mit Basiswinkeln der Größe w, die dritte schneidet im Trapez unten rechts ein rechtwinkliges Dreieck
ab, das bei E ebenfalls einen Winkel der Größe w hat. Die von E ausgehende Spiegelungs-Strecke
unten rechts zeigt hier anders als in der vorhergehenden Gleitschau in Richtung des Kreis-Mittelpunktes.
In den ersten fünf Bildern reicht dann ein Billard-Pfad, um alle 5-Stern zu beranden. Ein weiterer Pfad
erzeugt in den Bildern 6 bis 11 auch die 11-Strerne und mit einem dritten Pfad wird in den Bildern 12
bis 17 dann der 9-Stern geschlossen, der allerdings auch hier unregelmäßig ist.