Es lebe die Geometrie!

Quadrupel von Kreisen, die sich paarweise berühren

Das Kreis-Problem von Apollonios von Perge (-265 bis -190) ist die Aufgabe, zu drei Kreisen einen vierten
mit Zirkel und Lineal zu konstruieren, der alle drei berührt.Wenn die drei gegebenen Kreise sich paarweise
untereinander berühren, vereinfacht sich diese Aufgabe deutlich. In der folgenden Gleitschau wird dies für
drei Kreise dargestellt, die sich paarweise von außen berühren, deren Inneres also paarweise disjunkt ist.
Sieh dazu auch die Seite ' Satz von Poncelet nicht-euklidisch'.

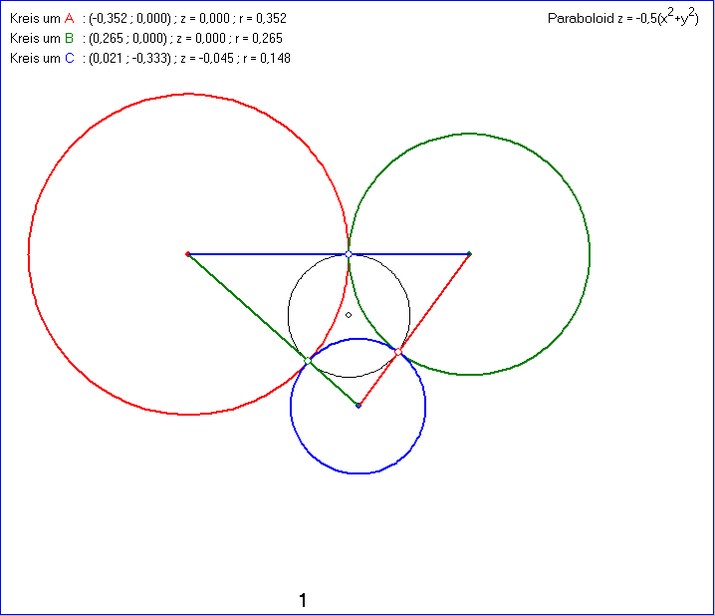
Bild 1 der Gleitschau zeigt drei sich paarweise außen berührende Kreise KA, KB und KC, deren Zentren
A, B und C ein Dreieck mit den Seitenlängen , und in der xy-Ebene
bilden. Die Berührpunkte von KA, KB und KC sind dann die Punkte , in denen der Inkreis KZ die
Seiten berührt. Diese Berührpunkte sind die inneren Ähnlichkeits-Zentren I*, J* und L* der drei
Kreise. Die zugehörigen äußeren Ähnlichkeits-Zentren I, J und L ergeben sich als Schnittpunkt einer
Seite-Gerade j mit der Verbindungs-Geraden der beiden inneren Ähnlichkeits-Punkte, die nicht auf j
liegen. Sie inzidieren mit der in Bild 2 blau unterlegten Ähnlichkeits-Achse g. L liegt hier außerhalb des
Bildes. In Bild 3 werden die Kreise KI, KJ und KL hinzugefügt, die mit dem inneren Ähnlichkeits-
Punkt inzidieren, der mit I bzw. J bzw. L auf der gleichen Seiten-Gerade liegt. KI, KJ und KL haben
zwei Punkte gemeinsam, von denen einer außerhalb des Bildes liegt.

KI schneidet KZ orthogonal in I*. Da KZ den Kreis KA in J* und L* schneidet, ist die Gerade J*L*
Potenz-Gerade von KZ und KA. Darum schneidet KI auch KA orthogonal. Die Inversion an KI
bildet darum KA auf sich ab und vertauscht die Punkte J* und L*. Da I* bei dieser Inversion fest
bleibt, bildet sie KB auf KC ab und KC auf KB. Der Kreis K, der KA, KB und KC von außen
berührt, wird darum durch die Inversion an KI auf sich abgebildet, insbesondere bleibt sein
Berühr-Punkt mit KA fest. Dieser Berühr-Punkt muss darum der Schnitt-Punkt von KI mit KA
im Innern des Dreiecks ABC sein. Da Entsprechendes für KJ und KL gilt, ist K der Kreis KM1
in Bild 4 durch die Schnittpunkte von KI mit KA, KJ mit KB und KL mit KC, die im Innern von
ABC liegen. Die Daten zu KM1 sind oben rechts im Bild 4 angegeben. Darunter steht eine
Gleichung über einen algebraischen Zusammenhang zwischen den Radien des Berühr-Quadrupels
(KA;KB;KC;KM1), den Rene´ Descates (1566-1650) entdeckt hat und aus einem Brief an die
Prinzessiin Elisabeth von Böhmen übermittelt ist. Die Zahl 2 auf der rechten Seite der Gleichung
ist konstant für alle möglichen Kombinationen von KA, KB und KC , wenn KM1 diese Kreise
von außen berührt.

Im 5.Bild wird der Kreis KM2 hinzugefügt, den die Kreise KA, KB und KC von innen berühren.
Die Gleichung für KM1 ist übertragbar, wenn man die Krümmung durch
ersetzt. KM2 hat also eine Orientierung entgegengesetzt zu KM1. Das 6. Bild zeigt, dass Z mit M1
und M2 kollinear ist und auch mit den Berührpunkten von M1 und M2 an jeden der Kreise KA, KB
und KC. Im 7. Bild wird der Gergonne-Punkt G des Dreiecks hinzugefügt. Dies ist der gemeinsame
Punkt der Verbindungs-Geraden der Eckpunkte von ABC mit den Berühr-Punkten des Inkreises. Auch
G ist kollinear mit Z, M1 und M2. Die Gerade durch Z, G, M1 und M2. ist die Gleichheits-Achse zu KA,
KB und KC. Sie ist euklidisch orthogonal zur Ähnlichkeits-Achse.

Die signierten Krümmungen der beiden Berühr-Kreise KM1 und KM2 von KA, KB und KC sind die
Lösungen der quadratischen Gleichung mit der
Unbekannten kd. Wir bezeichnen diese Gleichung als 'Descartes-Gleichung'. Die Lösungen sind
. Es ist also und
.

Der Punkt M1 wird im Dreieck ABC als 'Punkt mit gleichem Umweg' bezeichnet. Denn die Differenzen
der Längen der Streckenzüge BM1C , CM1A , AM1B und der Seitenlängen BC , CA , AB sind gleich,
weil . Der Punkt M2 heißt auch
'isoperimetrischer Punkt' oder 'Punkt mit gleichem Umfang', denn hier gilt die Gleichung
. Die Kimberling-Nummern
in der Enzycopedia of triangle centers (ETC) sind X176 bzw. X175. KM1wird als 'innerer Soddy-Kreis'
bezeichnet nach Frederic Soddy (1877-1956) und KM2 als 'äußerer Soddy-Kreis'.

Während die ersten sieben Bilder der Gleitschau nur Punkte in der xy-Ebene darstellen, zeigen das 8.
und 9. Bild statt der Kreise KA, KB, KC, KM1 und KM2 die zugehörigen Ellipsen auf dem Paraboloid
Par, die sich aus den Kreisen durch Projektion parallel zur z-Achse auf Par ergeben. Diese sind
Schnittmengen der Ebenen mit Par, deren Pole bezüglich Par die statt der Kreis-Zentren eingezeichneten
Raum-Punkte RA, RB, RC, RM1 und RM2 sind. Die beiden Tetraeder mit den Eckpunkten RA, RB,
RC, RM1 und RA, RB, RC, RM2 sind durch breite weiß gefüllte Strecken markiert, wobei die Strecken
durch RM2 bis zu den Berührpunkt der zugehörigen Geraden mit Par verlängert wurden. Jede der
Geraden zu den neun weiß gefüllten Strecken berührt Par in genau einem Punkt. Par ist für das flache
Tetraeder mitden Eckpunkten RA, RB, RC, RM1 Kanten-Quadrik mit Berühr-Punkten im Innern der
Kanten und das Tetraeder mit den Eckpunkten RA, RB, RC, RM2 Kanten-Quadrik mit Berühr-Punkten
auf der Verlängerung der Kanten durch RM2. Im 10. Bild wurden die Kreise in der xy-Ebene hinzugezeichnet.

Zur Berechnung der baryzentrischen Koordinaten der Soddy-Kreise:

Ein baryzentrische Koordinaten-Tripel des Inkreis-Zentrums Z vom Dreieck ABC mit den Seitenlängen
a, b und c hat unnormiert die einfache Forn (a;b;c) und normiert die Form (a;b;c) /(a+b+c), denn
wenn man die kartesischen Koordinaten-Paare der Punkte A, B, C und Z ebenfalls mit A, B, C und Z
bezeichnet, ist . Zur b-Normierung eines unnormierten baryzentrischen
Tripels teilt man durch die Summe der Komponenten, damit im Ergebnis die Komponenten-Summe 1 ist.
Siehe dazu die Pdf-Datei ' Schwerpunktskoordinaten in der Dreiecksgeometrie'. Man wendet also die
Funktion an.
Wenn ra, rb und rc die Radien dreier Kreise mit dem Zentren A, B und C sind, die sich paarweise von
außen berühren, dann ist rb + rc = a, rc + ra = b und r + rb = c, folglich ra = (-a + b + c)/2),
rb = (a - b + c)/2) und rc = (a + b - c)/2). Der Berührpunkt I* des Inkreises mit der Seite BC teilt
diese im Verhältnis rc/rb. Darum ist (0 ; rc ; rb) unnormiertes baryzentrisches Tripel von I*. Wegen
ist auch (0 ;1/rb ; 1/rc) unnormiertes baryzentrisches Tripel
von I*. Entsprechend ergeben sich für die Berührpunkte J* und L* die Tripel (1/ra ; 0 ; 1/rc) und
(1/ra ;1/ rb ; 0). Der Gergonne-Punkt G hat darum das unnormierte Tripel (1/ra ; 1/rb ; 1/rc). Da die
Zentren M1 und M2 der Berührkreise von KA, KB und KC auf der Geraden durch Z und G liegen,
sind ihre Tripel Linearkombinationen der normierten Tripel nb((a;b;c)) und nb((1/ra ; 1/rb ; 1/rc)).

Wir bezeichnen im Folgenden wie schon am Ende der vorangehenden Seite ' Winkel und Abstand' die
signierte Krümmung eines Kreise vom Radius rx mit kx.

Satz : Die Krümmungen dreier paarweise außen berührenden (reellen) Kreise mit den Zentren A, B und C
seien ka, kb und kc. km1 sei die Krümmung des zugehörigen inneren Soddy-Kreises mit dem Zentrum M1.
ka, kb, kc und km1 seien positiv.
Dann ist und
ist baryzentrisches Tripel von M1.

km1 ist eine der beiden Lösungen, die sich ergeben, wenn man die oben angegebene Descartes-Gleichung
nach kd auflöst. Die andere Lösung ist km2. Wenn man km1 in dem Tripel m1 durch km2 ersetzt, ergibt
sich ein baryzentrisches Tripel m2 für das Zentrum des äußeren Soddy-Kreises.

Die Summe der Komponenten von m1 ist , wobei der Flächeninhalt des Dreiecks ABC ist.
Die Summe der Komponenten von m2 ist .
Eine alternative Darstellung des baryzentrische Tripels von M1 ist und für M2
, wobei ar, br und cr die Radien der Ankreise von ABC sind. Die normierte Form
dieser Tripels stimmt also mit nb(m1) bzw. nb(m2) überein.
M1 teilt die Strecke vom Inkreis-Zentrum zum Gergonne-Punkt im Verhältnis km1/(ka+kb+kc)-1.
M2 teilt die Strecke vom Inkreis-Zentrum zum Gergonne-Punkt im Verhältnis km2/(ka+kb+kc)-1.

Zum Beweis des Satzes kann man zeigen, dass das Quadrat des euklidischen Abstands der Punkte
A und M1 gleich ist, wobei Analoges für B und C gilt. Der Vektor
hat die Komponenten-Summe Null und die Länge . Das Quadrat der Länge berechnet man mit
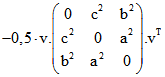, wobei hier die Ersetzung , und
sinnvoll ist (siehe dazu das Kapitel 12 in der oben angegebenen Pdf-Datei). Eine
längere Rechnung zeigt dann .

Zur algebraischen Lösung des apollonischen Kreis-Problems für drei paarweise außen
berührende Kreise:

Wir gehen von drei reellen Kreisen KA, KB und KC zu den Raum-Punkten (xa;ya;za), (xb;yb;zb) und
(xc;yc;zc) aus, deren Krümmungen ka, kb und kc positiv sind. Wir betrachten im Anschluss an den
Schluss der vorangehenden Seite ' Winkel und Abstand' die Matrizen
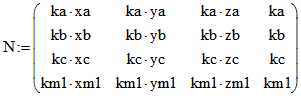, und .
Q ergibt sich aus der am Schluss der vorangehenden Seite definierten Matrix Q, indem man u = v = w = 2
setzt. ist die oben definierte Descartes-Gleichung.
Wenn sich KA, KB, KC und KM1 paarweise von außen berühren und die Krümmungen positiv sind,
ist der Funktionswert der Maßfunktion f für alle Paare aus den f-normierten Quadrupeln zweier Zeilen
von N gleich -1, die Schnittwinkel-Größe also 180°. Darum gilt und folglich .
Hier ist . Da die letzte Zeile (0;0;1;0) von M mit der letzten Zeile
von übereinstimmt, folgt aus die Descartes-Gleichung . km1 ist dann eine positive Lösung dieser
Gleichung. Die Gleichungen , und sind jeweils linear in xm1 bzw. ym1 bzw. zm1.
Man errechnet durch Lösung dieser Gleichungen die Koordinaten des Raum-Punktes von KM1. Damit
gilt
.
Wenn die Descartes-Gleichung noch eine zweite positive Lösung hat, liefert diese nach dem gleichen
Verfahren die Krümmung vom zweiten Soddy-Kreis und die Gleichung des Raum-Punktes gilt analog.
Wenn die Krümmung der zweiten Lösung negativ ist, bedeutet dies, das KM2 von KA, KB und KC
von innen berührt wird, die Schnittwinkel-Größe 0° beträgt und für das f-normierte Quadrupel
gilt: .
Dann ist aber wegen wie in unserem Ansatz verlangt
.


.

Zum komplexen Satz von Descartes :

Beim komplexen Satz von Descartes wird die Descartes-Gleichung über die Krümmungen der Kreise
KA, KB, KC , KM1 (oder KM2 ) durch eine ähnliche Gleichung für die Mittelpunkte erweitert, wobei
die Zentren mit den komplexen Zahlen , , und
( oder ) dargestellt werden. Es gilt dann folgender

Satz : KA, KB und KC seien paarweise sich von außen berührende Kreise mit den positiven
Krümmungen ka, kb und kc und den Zentren pa, pb und pc. KD sei der zugehörige
innere oder äußere Soddy-Kreis mit der Krümmung kd und dem Zentrum pd.
Dann gelten die quadratischen Gleichungen
und
.
(Die zweite Gleichung war Descartes noch nicht bekannt.)

Zum Beweis benutzen wir in der vorangehenden Gleichung für Tripel nur die Gleichung für die erste
und zweite Komponente, bei denen auf der rechten Seite Null steht und addieren zum Term für die
erste Komponente auf der linken Seite das i-fache des entsprechenden Terms für die zweite
Komponente und erhalten

Die Auflösung dieser Gleichung nach pd und die Lösung
der Krümmungs-Gleichung nach kd setzen wir in den
Term ein
und erhalten für beide Vorzeichen vor der Wurzel zu den Krümmungen der Soddy-Kreise



Hierbei ist bemerkenswert, dass nur noch die Differenzen der Kreis-Zentren vorkommen, so dass
der Term invariant gegen Verschiebungen des Dreiecks ist. Es muss gezeigt werden, dass er Null ist.
Die Ersetzung
ergibt dann

Die Ersetzung und

zeigt schließlich das gewünschte Ergebnis Null.



.