Es lebe die Geometrie!

Einschaliges Hyperboloid 1

Auf dieser Seite wird das Hyperboloid gezeigt, das sich mit der auf der vorhergehenden Seite ' Ceva'
dargestellten Konstruktion aus dem Standard-Viereck ABCD ergibt, dessen Koordinaten unten links
in Bild erscheinen.

Diese Animation zeigt das einschalige Hyperboloid zur Teilverhältnis-Konstanten tvk = 2, das entsteht,
wenn man die rauten-ähnlichen Vierecke zwischen den Regulus-Geraden ausfüllt, deren Konstruktion auf
der vorhergehenden Seite ' Ceva' erklärt wurde. Dabei wird die Vorderseite des Hyperboloids, die der
Sehstrahl zuerst trifft, in Blautönen gezeichnet und die Rückseite in Gelbtönen. Der Augenpunkt wird
zunächst in die z-Achse gedreht. In der Vogel-Perspektive fallen dann die Geraden AB und DA sowie die
Geraden BC und CD zusammen auf Tangenten des magentafarbenen Einheitskreises. Anschließend werden
die Projektionsbilder der Strecken AB und BC zu einem Tangenten-Quadrat ergänzt. Der blau gezeichnete
Umkreis dieses Tangenten-Quadrats enthält 4n Schnittpunkte von Regulus-Geraden, wobei n = 8 die Anzahl
der Teilstrecken ist, in welche die Strecken AB und BC bei der Konstruktion der Geraden aufgeteilt werden.
Beim folgenden Rückweg des Augenpunktes wird das Tangenten-Quadrat in zwei Vierecke auseinander
gezogen, die symmetrisch zur xy-Ebene liegen. Wir nennen diese Figur mit 12 Schnittpunkten
'Ergänzung des Basisvierecks'.

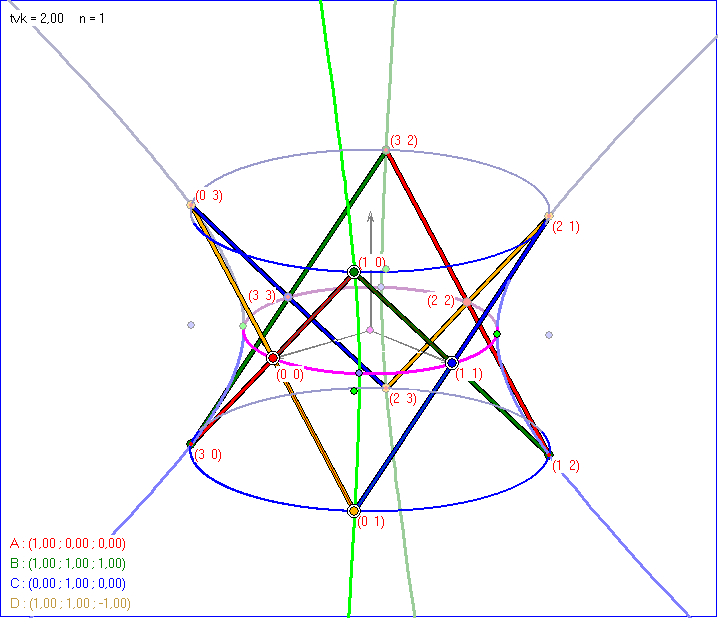
Die Ergänzung des Basis-Vierecks A = (1 ; 0 ; 0) = Hyp(0;0), B = (1 ; 1 ; 1) = Hyp(1;0),
C = (0 ; 1 ; 0) = Hyp(1;1), D = (1 ; 1 ; -1) = Hyp(0;1) hat die zusätzlichen Punkte
E = Hyp(2;1 ), F = Hyp(1;2 ), G = Hyp(3;0 ), H = Hyp(0;3 ), I = Hyp(2;2 ), J = Hyp(3;3 ),
K = Hyp(3;2 ) und L = Hyp(2;3 ). Die Gleitschau zeigt diese Paare (r ; s) der
Hyperboloid-Koordinaten r und s. Ausgehend von dem Basis-Viereck, der Teilverhältnis-
Konstante tvk und dem Mittelpunkt des Hyperboloids ergeben sich
diese Punkte folgendermaßen :
, , , , ,
und . Dabei benutzen wir die großen Buchstabe nicht nur für die Punkte
selbst, sondern auch für ihre Koordinaten-Tripel. E bzw. F teilt CD bzw. CB im Verhältnis -tvk.
G bzw. H entsteht durch Spiegelung von B bzw. D an A, I bzw. J durch Spiegelung von A bzw. C
an M und K bzw. L durch Spiegelung von F bzw. E an I. In der Gleitschau wird die Ergänzung der
Basis-Vierecks in drei Ansichten gezeigt, bei denen der Augenpunkt auf der Ursprungsgeraden durch
den Punkt (-1;1;0) bzw. (1;1;0) bzw. (0;0;1) liegt. Dabei ist die Lage der Punkte insbesondere im
Hinblick auf die drei Kegelschnitte von Interesse.

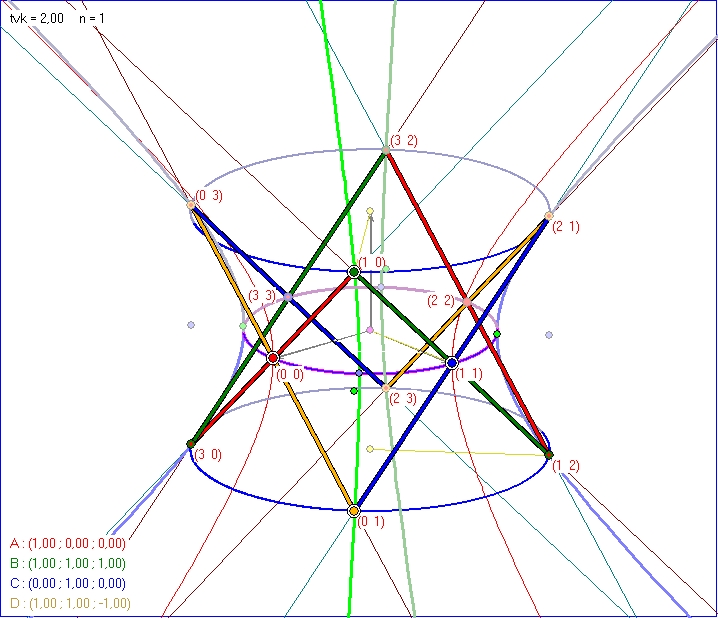
Die Punkte D = Hyp(0;1), F = Hyp(1;2 ), L = Hyp(2;3 ), und G = Hyp(3;0 ), für die s kongruent r+1
modulo 4 gilt, liegen auf einer der blauen Kurven, die im Fall tvk = 2 ein Kreis ist. Sie liegt in der Ebene mit dem
Quadrupel (2-tvk ; 0 ; -tvk ; -2). Die Punkte B = Hyp(1;0), E = Hyp(2;1 ), K = Hyp(3;2 ) und H = Hyp(0;3 )
mit r kongruent s+1 modulo 4 liegen in der Ebene mit dem Quadrupel (2-tvk ; 0 ; tvk ; -2).Wir nennen diese
beiden dick gezeichneten blauen Kurven 'Basis-Kegelschnitte'. Für alle Werte der Teilverhälttnis-Konstante
tvk sind sie Kegelschnitte, die sich hier nicht als ebene Schnitte eines Kegels sondern eines Hyperboloids zeigen.
In der Gleitschau werden neben tvk = 2 die Fälle tvk =2,5 ; 1,75 ; 1,5; 1,1; 0,9; 0,5; 0,2; -0,2; -1,0 ; -2,0
und -2,5 gezeigt, in einem zweiten Durchlauf auch in der Vogel-Perspektive.

Die neben tvk in der Gleitschau oben links angezeigte Zahl n gibt die Anzahl der Teilstrecken an, in welche
die Strecken des Basis-Vierecks ABCD bei der Konstruktion der Regulus-Geraden unterteilt werden.
Mit wachsendem n treten neue Schnittpunkte auf weiteren blauen Kurven auf. Sie sind auch Schnittkurven
von Ebenen mit dem Hyperboloid, folglich Kegelschnitte. Sie bilden zusammen das von den beiden
Basis-Kegelschnitten erzeugte Kegelschnitt-Büschel, zu dem auch die magentafarbene Kurve gehört.
Wenn d und e die Quadrupel der Ebenen sind, in denen die Basis-Kegelschnitte liegen, also
d = (2-tvk ; 0 ; -tvk ; -2) und e = (2-tvk ; 0 ; tvk ; -2) gilt, dann gibt es zu jeder dieser Kurven eine
Zahl r, so dass das Quadrupel der zugehörigen Ebene ist.
Die blaue Kurve durch einen Punkt Hyp(r;s) liegt in der Ebene mit dem Quadrupel
. Wir nennen sie ' 1. Diagonale durch Hyp(r;s) '.
Ein zweiter Punkt Hyp(r';s') liegt also genau dann auf der gleichen Kurve, wenn .

Der Kegelschnitt in der Ebene zum Quadrupel
geht ebenfalls durch den Punkt Hyp(r;s) . Ein zweiter Punkt Hyp(r';s') liegt also genau dann auf der gleichen
Kurve, wenn . Wir nennen sie ' 2. Diagonale durch Hyp(r;s) '. Sie erscheinen in der Gleitschau
als rote Kurven.

Die 1. und 2. Diagonale durch Hyp(r;s) liegen in Ebenen, die H-orthogonal zueinander sind. beide sind auch
H-orthogonal zu den Tangenten im Punkt Hyp(r;s), folglich auch zu den beiden Regulus-Geraden Gx(r) und
Gy(s). Die Schnittgerade dieser Ebenen geht durch Hyp(r;s) und den Punkt N zum Tripel
. N liegt für alle r und s auf der Parallelen zur z-Achse durch den Punkt
N0 zum Tripel . Der Mittelpunkt M von QH zum Tripel teilt die
Strecke AN0 im Verhältnis . In der Gleitschau sind die Strecken von einigen Punkten Hyp(r;s) zum
zugehörigen Punkt N gelb eingezeichnet. Dabei ist im zweiten Durchlauf in Vogel-Perspektive bemerkenswert,
dass die Geraden, auf denen in dieser Ansicht die roten und gelben Strecken gemeinsam liegen, in einem Punkt
zusammenlaufen.

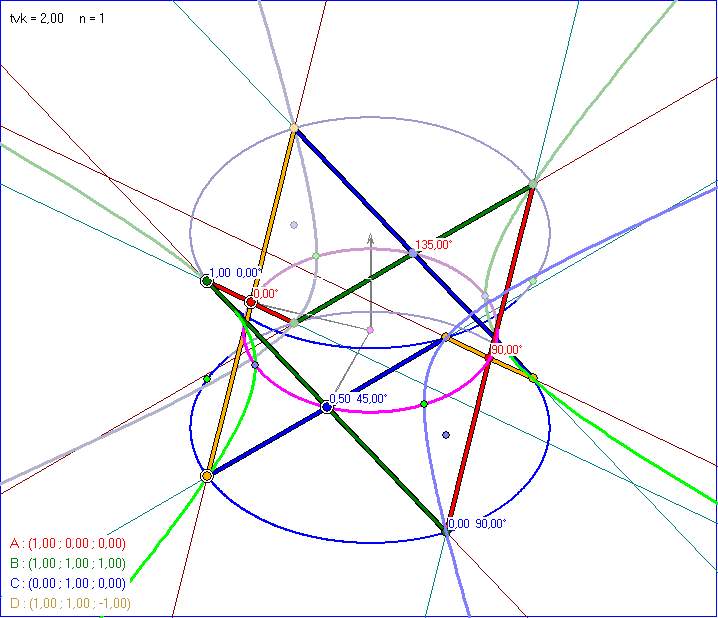
Wenn d und e die Quadrupel der Ebenen sind, in denen die Basis-Kegelschnitte liegen, dann gibt es also
zu jeder der blauen Kurven eine Zahl r, so dass das Quadrupel der zugehörigen Ebene ist.
Die Gleitschau soll den Parameter r veranschaulichen. Dazu sind an die Schnittpunkte der magentafarbenen
Kurve mit den Regulus-Geraden die Winkelgrößen in roter Schrift angeheftet, die sich entsprechend
der vorangehenden Seite ' Ceva' bei der Konstruktion der Regulus-Geraden ergeben. Für die Teilverhältnis-
Konstante tvk = 2 ist dies der halbe Mittelpunktwinkel zum Bogen auf dem Einheitskreis, der beim Punkt
A beginnt. Zu den Schnittpunkten der Regulus-Geraden mit der Geraden BC ist der Parameter r zugefügt,
der zu dem blauen Kegelschnitt k durch diesen Punkt gehört. Daneben steht die Winkelgröße .
Man kann als das Verhätnis ansehen, in dem die Ebene zu k die der Basis-Kegelschnitte teilt. Der
Vergleich dieser Winkel mit den roten Winkelgrößen zeigt Übereinstimmungfür k zwischen den Basis-
Kegelschnitten, und sonst einen negativen Wert, der sich ergibt, wenn von der zugehörigen roten
Winkelgröße 180° abgezogen wird.

Diese Animation zeigt Quadriken zur Teilverhältnis-Konstanten tvk im Bereich von 2 bis 0,3 in
verschiedenen Ansichten. Dabei hat die magentafarbene Schnittkurve mit den Regulus-Geraden 4n
Schnittpunkte, wobei n = 32. Zuerst wird tvk von 2 bis 0,3 verkleinert, dann der Augenpunkt bei
konstantem tvk-Wert in die Vogel-Perspektive gedreht, schließlich tvk auf den Wert 2 erhöht und
dann der Augenpunkt in seine Ausgangslage zurückgedreht. In einem zweiten Durchlauf wurden bei
n = 10 die blauen Kegelschnitte zugefügt.

Das letzte Standbild der Gleitschau verdeutlicht, wie man sich im Fall des Hyperboloids zu tvk = 2
die Menge der unendlich fernen Punkte dieser Quadrik vorstellen kann. Man betrachte dazu eine Gerade
g durch den Ursprung und einen Punkt P der roten Kurven, die sich beim Schnitt von QH mit einer Ebene
durch die z-Achse ergibt. Sie ist in dieser Ebene eine Hyperbel, zeigt sich aber in der Vogel-Perspektive
geradlinig. Wenn P immer weiter ins Unendliche rückt, nähert sich g einer Asymptoten der Hyperbel. Der
unendlich ferne Punkt auf g kann darum als Punkt des projektiven Abschlusses des Hyperboloids gesehen
werden. Die größer werdenden blauen Kreise des Schnitts mit Ebenen parallel zur xy-Ebene machen es
plausibel, dass man die Menge der unendlich fernen Punkte von QH als Kreis in der unendlich fernen
Ebene ansieht. Man stellt sich dazu den Doppel-Kegel aller Asymptoten der roten Hyperbeln vor. Er hat
hier den Öffnungswinkel 90°.

Im projektiven Abschluss des affinen Raums der Punkte-Tripel (x ; y; z) beschreibt man die unendlich
fernen Punkte durch Quadrupel (x ; y ; z ; 0). Eine Ebene, die im affinen Raum die Gleichung
hat, wird als Quadrupel durch [a ; b , c ; d] beschrieben. Analog zu den
Koordinaten-Ebenen x = 0, y = 0 und z = 0 mit den Quadupeln [1 ; 0 ; 0 ; 0], [0 ; 1 ; 0 ; 0] und
[0 ; 0 ; 1 ; 0] beschreibt man die unendlich ferne Ebene durch u = 0 oder das Quadrupel [0 ; 0 ; 0 ; 1].
Das Hyperboloid des letzten Bildes der Gleitschau hat im affinen Raum die Gleichung
oder . Ersetzt man hier x durch , y durch und
z durch und multipliziert mit u, erhält man die Gleichung von QH im
projektiven Raum. Für die Schnittmenge der unendlich fernen Ebene ergibt sich die Kreis-Gleichung
.