Es lebe die Geometrie!

Höhen und Isohypsen bei Penrose-Kachelungen

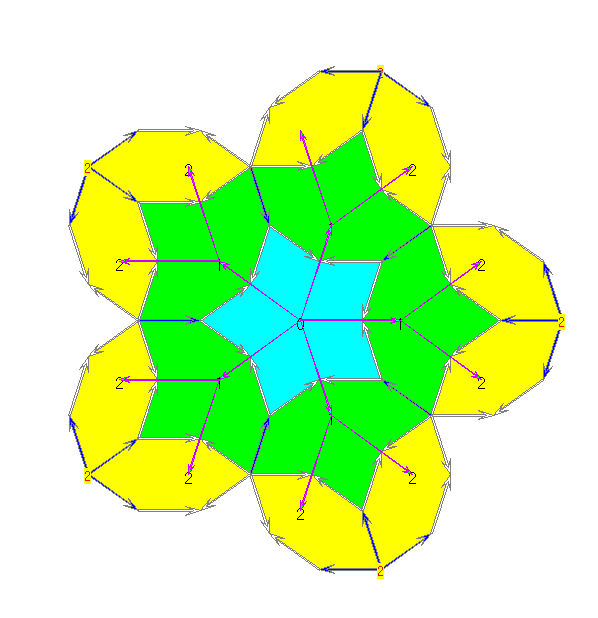
In dieser Gleitschau wurden zu Stern-, Kronen- und Boot-Kacheln 2. und 3. Stufe rotviolette
'Flächen-Pfeile' gezeichnet, die Zentren benachbarter Kacheln 1.Stufe verbinden. Das Verhältnis
der Länge dieser Pfeile zu der Länge der Kachel-Seiten 1. Stufe ist die große goldene Zahl
. Jeder Flächen-Pfeil wird im goldenen Schnitt von einem Punkt geteilt, in dem
zwei graue Rand-Pfeile mit der Spitze zusammentreffen. Dabei liegt dieser Punkt näher an der
Spitze des Flächen-Pfeils als an seinem Ausgangspunkt. Alle Punkte, in denen die Spitzen zweier
Rand-Pfeile zusammentreffen, liegen in einer vollständigen Kachelung der ganzen Ebene auf einem
Flächen-Pfeil. Vom Zentrum jeder Stern-Kachel 1.Ordnung gehen dabei fünf Flächen-Pfeile aus,
zum Zentrum jeder Boot führen zwei Flächen-Pfeile hin und vom Zentrum jeder Kronen-Kachel
gehen zwei Flächen-Pfeile aus und einer hat dort seine Spitze. Die Flächen-Pfeile bilden in einer
vollständigen Kachelung der ganzen Ebene die Rand-Pfeile einer Kachelung aus Stern-, Kronen-
und Boot-Kacheln, die wir '1. Inflation' der Ausgangs-Kachelung nennen. Die Flächen-Pfeile
dieser 1. Inflation sind die Richtungs-Pfeile zwischen den Spitzen der Boot-Kacheln 1. Stufe,
welche die Struktur der Kachelung darstellen, die sich durch die Kacheln 2. Stufe ergibt. Diese
Zusammenhänge lassen sich auf jede Kachelungsstufe übertragen. Zu der Kachelung aus den
Kacheln n-ter Stufe passt also die 2n -te Inflation der Ausgangs-Kachelung.

Die schwarzen ganzen Zahlen an den Kachel-Zentren legen eine 'Höhe' jeder Kachel 1.Stufe fest, die
sich folgendermaßen ergibt. Für die Mitte Z der zentralen Stern-Kachel wurde die Höhe 0 bestimmt,
entsprechend dem Normalhöhennull in der Geographie. Sei M das Zentrum einer Kachel 1. Stufe.
Es gibt von Z nach M einen Pfad aus Flächen-Pfeilen. Beim Durchlaufen dieses Pfads sei a bzw. b die
Anzahl der Flächen-Pfeile in Bewegungs-Richtung bzw. entgegengesetzt dazu. Dann ist die Höhe der
Kachel mit Zentrum M gleich der Differenz a-b. Diese Definition ist unabhängig von der Wahl des Pfads.
Kacheln gleicher Höhe mit einer gemeinsamen Seite sind genau die Kacheln, deren gemeinsamer
Seiten-Pfeil blau ist. Benachbarte Kacheln ohne gemeinsamen blauen Seiten-Pfeil unterscheiden sich
in ihren Höhen um 1.

Wenn der Stern-Kachel S 1. Stufe im Zentrum Z einer Kachel n-ter Stufe (n >0) die Höhe Null
zugeordnet wird, dann haben alle Kacheln 1. Stufe in diesem Kachel-Komplex eine Höhe größer
als Null. Daraus folgt, dass keine aus Stern-, Kronen-, und Boot-Kacheln gebildete Kachelung der
ganzen Ebene periodisch sein kann. Denn angenommen, es gibt eine von der identischen Abbildung
verschiedene Translation , die jede Kachel 1. Stufe auf eine dazu deckungsgleiche abbildet. n sei so
groß gewählt, dass die Stern-Kacheln und beide in der Stern-Kachel n-ter Stufe liegen. Dies
ist möglich, da jede dieser Kachelungen Stern-Kacheln jeder Stufe enthält. Da das Translationsbild
eines Pfades von nach S von S nach führt, gilt für die Höhen

im Widerspruch dazu, dass S die kleinste Höhe in dem Stern n-ter Stufe hat.

Zu den Kachel-Höhen passend wird auch für jeden Eckpunkt der Kachel-Ränder eine Höhe definiert.
Sie ist für einige dieser Punkte in den Zeichnungen rot angegeben. Für die Spitzen der Stern- und Kronen-
Kacheln ist die Höhe gleich der Kachel-Höhe. Für die Boot-Kacheln stimmt dies nur für die Spitze, von
dem der Richtungs-Pfeil der Boot-Kachel ausgeht. Für alle anderen Eckpunkte kann die Höhe so festgelegt
werden, dass in Richtung eines Rand-Pfeils die Höhe abnimmt, also anders als beim Flächen-Pfeil. Darum
ist die Höhe der Spitze des Richtungs-Pfeils von einer Boot-Kachel um 1 kleiner als die Höhe der Kachel.

P und Q seien zwei durch einen Seiten-Pfeil verbundene Eckpunkte. Dann hat einer der Punkte eine
geradzahlige Höhe und der andere eine ungeradzahlige. Außerdem: Von einem der beiden Punkte kommt
man zu seinen durch Pfeile verbundenen Nachbar-Punkten nur in Richtung geradzahliger Richtungs-Zahlen;
und vom anderen Punkt kommt man zu dessen Nachbar-Punkten nur über ungeradzahlige Richtungs-Zahlen.
Wie die Zuordnung dieser beiden Aspekte ist, hängt von der Wahl des Höhen-Nullpunktes ab.

In der Animation legt die Schildkröte Kronen- und Boot-Kacheln ab, die in jedem der entstehenden
drei Kränze die gleiche Höhe 3 bzw. 2 bzw. 1 haben. Dabei haben aufeinander folgende Kacheln stets
einen Seiten-Pfeil gemeinsam, der dadurch ausgezeichnet ist, dass seine Spitze auf den Ausgangpunkt
eines anderen Seiten-Pfeils trifft. In den auf die Animation folgenden Standbildern der Gleitschau sind
diese Pfeile blau gezeichnet. Da jede Kronen- oder Boot-Kachel zwei derartige Pfeile hat, ist der
Anschluss aufeinander folgender Kacheln eindeutig bestimmt. Zur Verdeutlichung der Form wurden
die Zentren aufeinander folgender Kronen-Kacheln jedes Kranzes durch eine rote Strecke verbunden.

Wir nennen diese Kränze 'Isohypsen' (Höhenlinien). Alle Isohysen haben fünf Symmetrie-Achsen
durch ihr Zentrum, bei denen der Winkel zwischen benachbarten Achsen die Größe 72° hat.

In den beiden Teile der Animation werden zwei verschiedene Formen der Isohypsen dargestellt.
Bei der 'Außen-Form' sind die Mittel-Spitzen der Kronen-Kacheln nach außen gerichtet und die
Boot-Kacheln nach innen, während es bei der 'Innen-Form' umgekehrt ist. Sie unterscheiden sich
durch die Abfolge der Kronen(K)- und Boot(B)-Kacheln. Die zugehörige Zeichenkette aus den
Zeichen 'K' und 'B' für eine Periode des Kranzes zur Höhe n sei Außen[n] bzw. Innen[n] genannt.
Der ganze Kranz entsteht durch die Verkettung von fünf gleichen Exemplaren Außen[n] bzw. Innen[n].
Außen[n] und Innen[n] ergeben sich aus folgender verketteten Rekursion ('+' bedeutet für Zeichenketten
das Hintereinandersetzen):

Außen[1]:='K'; Innen[1]:='BBK';

Außen[n]:=Außen[n-1]+Innen[n-1]+Außen[n-1];
Innen[n]:=Außen[n-1]+Innen[n-1]+Innen[n-1]+Innen[n-1]+Außen[n-1];

Vermutung: Jede Isohypse ist vom 'Typ' Außen[n] oder Innen[n]. Isohypsen gleichen Typs gehen
durch eine Punktspiegelung oder eine Verschiebung auseinander hervor.

Die Animation zeigt die Entstehung von Außen-Isohypsen zu den Höhen 1, 2, 3 und 4 und ihren
Zusammenhang mit einer Stern-Kachel der Stufe 4. In zwei Standbildern im Anschluss an die
Animation sind bei Stern-Kacheln der Stufe 4 und 5 nur die Kronen-Kacheln farbig markiert.
Hierbei werden Isohypsen dadurch erkennbar, dass Kronen-Kacheln genau dann zur gleichen
Isohypse gehören, wenn sie durch eine Kette von Kronen-Kacheln verbunden sind, bei der
benachbarte Kronen-Kacheln mindestens einen Punkt gemeinsam haben.

Die Animation zeigt die Entstehung von Innen-Isohypsen zu den Höhen 1, 2, 3 und 4 und ihren
Zusammenhang mit einem Kachel-Komplex, der sich aus fünf Boot-Kacheln der Stufe 4
zusammensetzt. Zwei der folgenden Standbilder zeigen entsprechende Komplexe zur Stufe 4
und 5, in denen nur die Kronen-Kacheln farbig gezeichnet sind, um dadurch alle Isohypsen
innerhalb des Komplexes zu zeigen.