Es lebe die Geometrie!

Kachelungen im Kreis-Modell, die mit Nachbar-Bewegungen
aus einem Dreieck mit der Signatur -1-2-3 erzeugt werden

Die Signatur -1-2-3 bedeutet, dass aus jeder Kachel K die Nachbarkacheln durch Spiegelung an den Seiten
entstehen. Wenn für K durch die halbe Pfeilspitze ein Durchlauf der Seiten gegen den Uhrzeigersinn festgelegt
ist, dann haben die Nachbarkacheln einen entgegengesetzten Durchlaufsinn. Sie sind dann 'negativ orientiert'.
Die Seite mit der halben Pfeilspitze hat dann die Nummer -1 und die folgenden im Uhrzeigersinn die Nummern
-2 und -3.
Das Ketten-Schema für die Spitze der Seite 3 ist dann . Die zweite
Zahl der Paare ergibt sich als Zahl der Signatur mit der Platznummer, die durch die erste Zahl gegeben ist, falls
sie positiv ist. Im Fall einer negativen ersten Zahl ist die Platznummer der Betrag davon und bei der zugehörigen
Zahl in der Signatur wird das Vorzeichen geändert. Aus der zweiten Zahl eines Paares ergibt sich auch hier die
erste des folgenden Paares durch Subtraktion von 1, wobei 0 mit 3 und -4 mit -1 identifiziert wird. Bei den
Bezeichnungen der Innenwinkel werden keine negativen Indizes benutzt. ist also in einem negativ orientierten
Dreieck die Größe des Innenwinkels bei der Spitze der Seite mit der Nummer -3. Im Ketten-Schema ergibt sich
der Index i des Winkels nach folgender Regel: i ist die Zahl rechts vom Pfeil, wenn diese positiv ist; andernfalls
ist i der Betrag der Zahl links vom Pfeil.

In dem obigen Ketten-Schema ergibt sich nach zwei Kacheln eine Periode. Darum kann ein Basis-Dreieck nur
dann zu einer Kachelung führen, wenn ein ganzzahliges Vielfaches von gleich 360° ist, also
mit einer ganzen Zahl n >1 gilt. Für die anderen Innenwinkel ergeben sich entsprechende Bedingungen, wobei
die ganzen Zahlen k, m und n im Nenner verschieden sein können, aber die Ungleichung
erfüllen müssen, da in der hyperbolischen Ebene keine Dreiecke existieren, für welche die Innenwinkelsumme
180° (oder mehr) beträgt. Wenn die drei Ecken-Bedingungen erfüllt sind, erzeugt ein Dreieck bei der Signatur
-1-2-3 eine Kachelung, d. h es kommt bei wiederholten Spiegelungen an Dreiecksseiten nicht zu
Überlappungen.

Die Spiegelungen an allen Dreieck-Seiten sind Automorhismen der Kachelung,
d. h. das Spiegel-Bild jeder Kachel gehört zur Kachelung.

Die Animation zeigt die Entwicklung einer Kachelung zur Signatur -1-2-3 bei einem Ausgangs-Dreieck
mit den Innenwinkeln 45°, 45° und 60°. Dabei werden nacheinander die Kränze bis zur Nummer 4
gezeichnet.

Das Bild Nr 2 in der Gleitschau zeigt die Kränze bis zur Nummer 2 im Beltrami-Klein-Modell.

Zu jedem Kranz bis zur Nummer 4 in den Bildern 2 bis 6 sind die Seiten des äußeren Randes zu Kreise
ergänzt worden, die orthogonal zum Einheitskreis sind. Da diese Kreise keine inneren Punkte des Kranzes
enthalten, ist die Vereinigung der Kränze bis zu einer beliebigen Nummer n stets hyperbolisch konvex. Der
Grund dafür liegt darin, dass an jedem äußeren Eckpunkt nur zwei oder drei Kacheln zusammentreffen und
die Innenwinkel-Summe an diesem Eckpunkt kleiner als 180° ist. Aus der Konvexität folgt, dass das Basis-
Dreieck eine Kachelung der ganzen hyperbolischen Ebene erzeugt, es also nicht zu Überlappungen kommt.

Im Bild 7 wurden in den Dreiecken der Kachelung die Höhen eingezeichnet. Es zeigt sich, dass sich die
Kreisbögen der Höhen in drei Scharen zu hyperbolischen 'Geraden' zusammenfügen. Die grün gezeichnete
Schar unterteilt die hyperbolische Ebene in kongruente Vierecke. Die blaue und die rote Schar erzeugt
eine Kachelung aus kongruenten Dreiecken und Vierecken.

Das Bild Nummer 8 zeigt für jedes Kachel-Dreieck das zugehörige hyperbolische Höhenfußpunkt-Dreieck.
Es ergibt sich daraus eine Kachelung aus jeweils kongruenten grünen Sechsecken, roten oder blauen
Achtecken, sowie rot-grün-blauen Dreiecken, wobei die Sechsecke und die Achtecke regelmäßig sind.

In den Bildern 9, 10 und 11 wurden Kacheln farblich zusammengefasst, die einen gemeinsamen Eckpunkt
mit der Nummer 1 bzw. 2 bzw. 3 haben. Dabei definieren wir als Nummer eines Eckpunkts einer Kachel
den Betrag der Nummer der Seite, zu der dieser Punkt die Spitze bildet. Es zeigt sich dann eine Kachelung
mit regelmäßigen Achtecken bei den Bildern 8 und 9 und mit Sechsecken beim Bild 10. Dabei gehen die
Kacheln durch Spiegelung an ihren Seiten auseinander hervor.

In den Bildern 12 bis 23 werden Kränze bis zur Nummer 2 dargestellt für ein Basis-Dreieck mit zwei Winkel-
Größen von 60° und einer dritten Größe mit ganzzahligem k mit . In Bild 24 und 25 sind
die Innenwinkel-Größen 60°, 10°, 45° bzw. 60°, 14°, 36°.

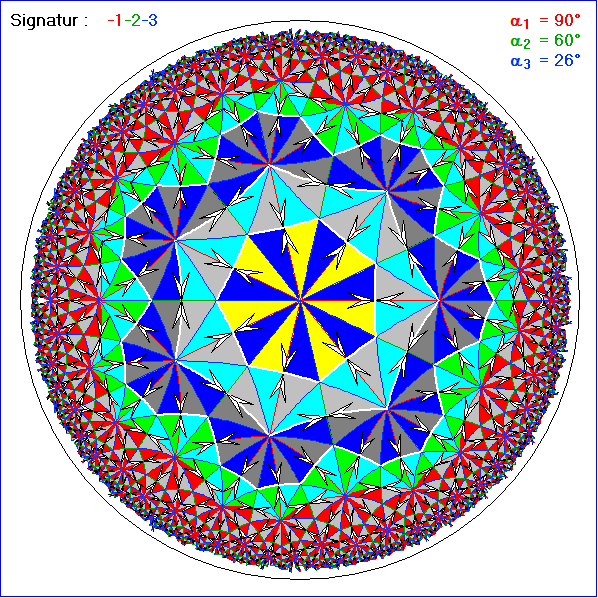
Die Bildfolge soll deutlich machen, dass rechtwinkligen Dreiecken bei der Signatur -1-2-3 zwar auch
Kachelungen erzeugen, dabei jedoch die Vereinigung von Kränzen bis zu einer Nummer n nicht notwendig
hyperbolisch konvex ist. Dies wird mit Hilfe der kleinstmöglichen Basis-Kachel gezeigt, die eine Kachelung
erzeugen kann. Sie hat die Innenwinkel 90°, 60° und , so dass die Summe möglichst nahe bei
180° liegt. Die Vereinigung der Kränze bis zur Nummer 2 ist konvex, auch die bis zur Nummer 4, nicht aber
die bis zur Nummer 3. Wenn man das Basis-Dreieck mit seinem Bild bei Spiegelung an der Seite 2 vereinigt
und das daraus entstandene gleichschenklige Dreieck als Basis-Dreieck wählt, erhält man dagegen stets
konvexe Kranz-Vereinigungen.

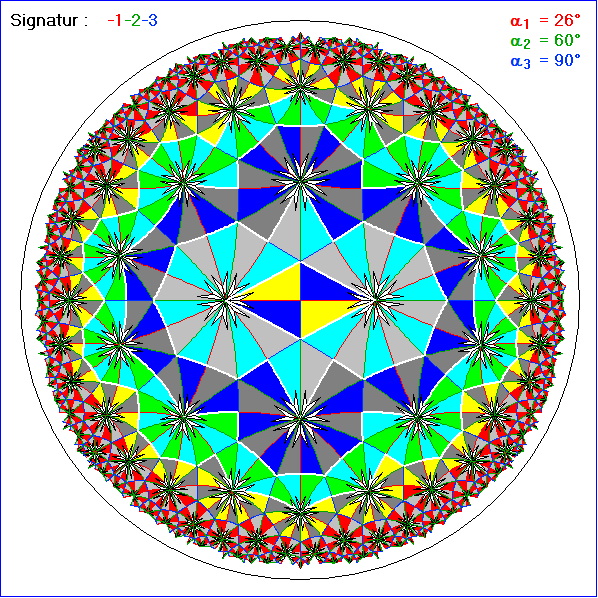
In dieser Bildfolge wurde das gleiche Basis-Dreieck wie in der vorhergehenden gewählt, jedoch mit dem
rechten Winkel im Zentzum des nullten Kranzes. Dann ist die Vereinigung der Kränze bis zur Nummer n
für n>0 nie konvex. Die nächste Bildfolge zeigt dazu eine einfache Korrektur.

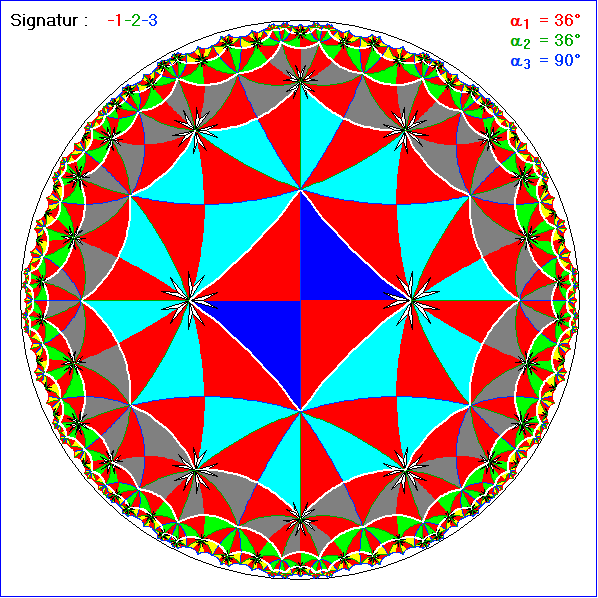
Die ersten beiden Bilder dieser Folge unterscheiden sich nur dadurch, dass in Richtung der Geraden y = x
und y = -x die weiße Umrandung anders gezeichnet ist. Dadurch wird in Bild 1 dem Kranz Nummer 2 an
vier Stellen ein Dreieck hinzugefügt, das eigentlich zum Kranz Nummer 3 gehört. Diese Änderung der
Zuordnung wird bei den Dreiecken wiederholt, die von den Geraden y = x oder y = -x getroffen werden.
Die Vereinigung der so korrigierten Kränze bis zu einer Nummer n ist dann stets hyperbolisch konvex.

Diese Animation zeigt, wie sich das Bild der Vereinigung dreier Kränze verändert, wenn man das
Zentrum der Kränze aus dem Einheitkreis-Mittelpunkt verschiebt.