Es lebe die Geometrie!

Nicht-reguläre Fourier-Polygone

Auf dieser Seite werden Polygone PS(n ; m ; p) bzw. PC(n ; m ; p) mit m ungleich Null zu
folgender Drehpunktfunktion dargestellt:
bzw.

Dabei wird vorausgesetzt, dass n, m und p natürliche Zahlen sind mit n > 1 und n > m > 0. Damit
p-geschlossene Drehpunktkurven entstehen, darf für keine ganze Zahl k gleich oder
sein. Abgesehen von den Sprungstellen stimmen diese Funktionen mit folgenden
Treppenfunktionen überein: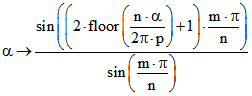
bzw.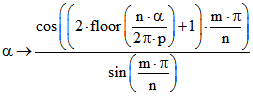

Dass diese Funktionen zwischen den Sprungstellen mit FS bzw. FC übereinstimmen, kann man im Fall
m ungleich Null und p = 1 folgendermaßen verstehen: Aus Satz 1 in der Pdf-Datei 'Fourier-Analyse
beliebiger Vielecke' ( https://www.vivat-geo.de/Pdf-Dateien/Fourierneck.pdf) folgt, dass die Funktion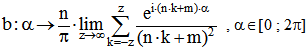
die gleichförmige Bewegung eines Punktes auf dem
Rand eines regelmäßigen Polygons mit der Eckenzahl n und der Überschlagungszahl m beschreibt. Dabei
liegt der Mittelpunkt des Polygons im Ursprung und die Bewegung verläuft gegen den Uhrzeigersinn.
Allerdings startet die Bewegung anders als in dem Text 'Fourier-Analyse beliebiger Vielecke' nicht im
Punkt (1 ; 0) sondern im Punkt, der daraus durch Streckung mit dem Faktor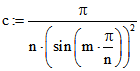
entsteht.

Die Ableitung

gibt die Funktion des Geschwindigkeitsvektors für diese Bewegung an. Da dieser sich nur an den Ecken
ändert, ist die Ableitung zwischen den Sprungstellen konstant. Dabei bestimmen die Konstanten die
komplexen Zahlen von Eckpunkten eines regelmäßigen n-Ecks mit der Überschlagungszahl m und dem
Zentrum im Ursprung, wobei die Hochachse Symmetrieachse mit einem Eckpunkt ist. Da bei der
Bewegung b der Rand des n-Ecks in der Zeit durchlaufen wird, ist der Betrag der Geschwindigkeit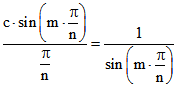
. Das reguläre n-Eck der Geschwindigkeiten hat darum die Seitenlänge 2.

Die Stufenhöhen von FC sind folglich die y-Werte der Eckpunkte eines regulären n-Ecks mit der
Überschlagungszahl m. Die Stufenhöhen von FS ergeben sich, wenn man die x-Werte der Eckpunkte
mit -1 multipliziert. Die Reihenfolge der Stufenhöhe erhält man dabei folgendermaßen: Man startet einen
Umlauf auf dem Rand dieses Geschwindigkeits-Polygons in dem Punkt der positven y-Halbachse, der in
der Mitte einer Polygon-Seite liegt, und durchläuft den Rand anschließend gegen den Uhrzeigersinn.
Darum sind die x-Werte bzw. y-Werte der Eckpunkte des Geschwindigkeits-Polygons die Werte der
Funktion 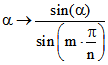bzw. 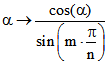in den Mitten der Intervalle, die sich ergeben, wenn
man das -Intervall gleichmäßig in n Teile teilt. Da die Summe der Quadrate des x-Werts und
des y-Werts stets das Quadrat des konstanten Geschwindigkeitsbetrags angibt, ist diese Summe für alle
Eckpunkte gleich 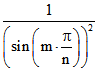. Außerdem gibt es einen Zusammenhang zwischen den Längen
und der Seiten bei den Polygonen PS(n ; m ; p) und PC(n ; m ; p) zum gleichen Richtungswinkel
und der Seitenlänge 2 des Geschwindigkeits-Polygons. Denn ist eine Sprungstelle im Graph der
Drehpunktfunktionen FS und FC, deren Sprunghöhe die Seitenlänge bzw. angibt.
Andererseits ist die Differenz der x-Werte von aufeinander folgenden Punkten im Geschwindigkeits-
Polygon, und die Differenz der y-Werte. Darum ist stets .

Die Herleitung dieser Aussagen setzt voraus, dass p = 1 ist. Für p > 1 übertragen sie sich mit Hilfe einer
Streckung mit dem Faktor p in Richtung der Rechts-Achse des Graphen der Drehpunktfunktion.

In der Animation wird die Fourier-Approximation des Polygons PS(5,2,1) gezeigt. Die fünf
Näherungsfunktionen der Drehpunktfunktion des Polygons sind:
,
,
,
und
.
In der dritten bis fünften Periode der Animation ist zum blauen Graph der Drehfunktion in grauer Farbe
der Graph von 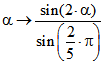hinzugezeichnet und darauf die Punkte markiert, die zu den Mitten der
Unterteilung des Definitions-Intervalls in fünf gleich große Teil-Intervalle gehören. Jeder dieser
Punkte ist die Mitte einer Stufe im Graph der Drehpunktfunktion des Polygons PS(5,2,1).

Die Animation zeigt den entsprechenden Ablauf wie in der vorherigen für das Polygon PC(5 ; 2 ; 1).
Bei den Näherungsfunktionen ist die Sinus-Funktion durch die entsprechende Kosinus-Funktion ersetzt.
Zum blauen Graph der Drehpunktfunktion ist teilweise der graue Graph von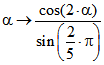
hinzugezeichnet. (Hierbei darf im Nenner 'sin' nicht durch 'cos' ersetzt werden.)

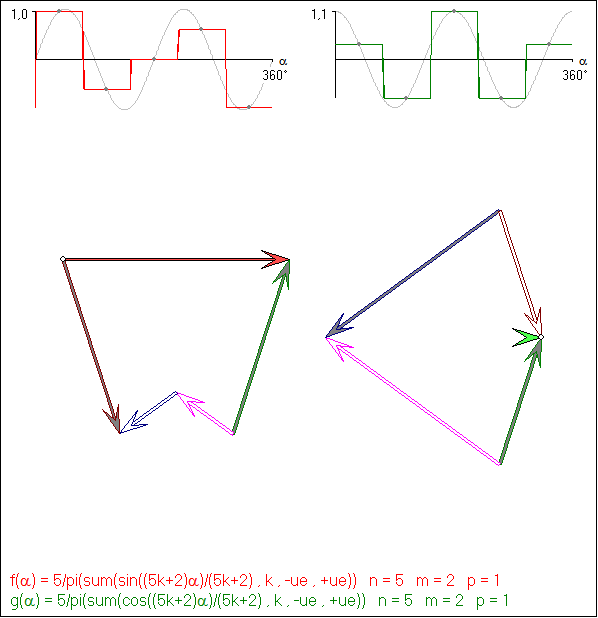
Die Gleitschau zeigt paarweise die Polygone PS(n ; m ; p) und PC(n ; m ; p). Dabei wurden die
Seiten durch Pfeile markiert, welche die zugehörige Richtung angeben. Es kommen nur Richtungswinkel
vor, die ganzzahlige Vielfache von sind. Seiten zum gleichen Richtungswinkel sind bei PS(n ; m ; p)
und PC(n ; m ; p) gleichfarbig berandet, Die Summe der Quadrate ihrer Längen ist stets 4. (Die Maßstäbe
sind von Bild zu Bild nicht gleich, wohl aber innerhalb eines Bildes.) Wenn ein Pfeil zu einer Seite mit negative
Länge gehört, ist er grau gefüllt gezeichnet, sonst weiß gefüllt. Alle Polygone haben die Umfangslänge Null.

Mit wachsender Eckenzahl n bei gleichen Werten für m und p nähern sich die Polygone PS(n ; m ; p) und
PC(n ; m ; p) immer mehr den zueinander kongruenten Drehpunktkurven zur Drehpunktfunktion
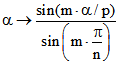und 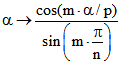. Für p = 1 sind dies {-m ; m}-Zykloiden, also z.B. für m = 2
eine Astroide und für m = 3 eine Steiner-Zykloide. Für p =2 und m = 1 ergibt sich eine Nierenkurve
(Nephroide) und für p = 3 und m = 1 eine Herzkurve (Kardioide).